Isometrische transformaties

De isometrische transformaties Het zijn veranderingen in positie of oriëntatie van een bepaalde figuur die de vorm of grootte hiervan niet veranderen. Deze transformaties zijn ingedeeld in drie typen: vertaling, rotatie en reflectie (isometrie). Over het algemeen kunnen geometrische transformaties een nieuwe figuur maken van een andere gegeven.

Een transformatie in een geometrische figuur betekent dat deze op een of andere manier aan enige verandering werd onderworpen; dat wil zeggen, het werd gewijzigd. Volgens de zin van het origineel en het soortgelijke in het vlak kunnen geometrische transformaties worden ingedeeld in drie typen: isometrisch, isomorf en anamorf.

Kenmerken van isometrische transformaties

- Isometrische transformaties treden op wanneer de grootten van de segmenten en hoeken tussen de oorspronkelijke figuur en de getransformeerde figuur worden bewaard.

- In dit type transformatie is de vorm of grootte van de figuur niet gewijzigd (ze zijn congruent), het is slechts een verandering van positie hiervan, hetzij in de oriëntatie of in de zin. Op deze manier zullen de initiële figuur en de finale vergelijkbaar en geometrisch congruent zijn.

- Isometrie verwijst naar gelijkheid; dat wil zeggen, dat geometrische cijfers isometrisch zullen zijn als ze dezelfde vorm en grootte hebben.

- In isometrische transformaties is het enige dat kan worden waargenomen een verandering van positie in het vlak, een rigide beweging treedt op dankzij welke de figuur van een beginpositie naar een finale gaat. Deze figuur wordt homologe (vergelijkbaar) van het origineel genoemd.

- Er zijn drie soorten bewegingen die een isometrische transformatie classificeren: vertaling, rotatie en reflectie of symmetrie.

Soorten isometrische transformaties

Door vertaling

Zijn die isometrieën die het in een rechte lijn kunnen verplaatsen alle punten van het vlak in een specifieke richting en afstand.

Wanneer een figuur wordt getransformeerd door vertaling, verandert deze niet zijn oriëntatie in relatie tot de initiële positie, noch verliest het zijn interne maatregelen, de metingen van zijn hoeken en zijden. Dit type verplaatsing wordt gedefinieerd door drie parameters:

• Een adres, dat horizontaal, verticaal of schuin kan zijn.
• Een richting, die links, rechts, omhoog of omlaag kan zijn.
• Afstand of grootte, die de lengte is die van de beginpositie is tot de finale van elk punt dat beweegt.

Kan u van dienst zijn: Curtosis: definitie, typen, formules, waarvoor bijvoorbeeld

Om een ​​isometrische transformatie als gevolg van vertaling te hebben, moet deze voldoen aan de volgende voorwaarden:

• De figuur moet altijd al zijn afmetingen behouden, zowel lineair als hoekig.
• De figuur verandert zijn positie niet ten opzichte van de horizontale as; dat wil zeggen, zijn hoek varieert nooit.
• Vertalingen zullen altijd in één worden samengevat, ongeacht het aantal vertalingen.

In een vlak waar het midden een punt is of, met coördinaten (0,0), wordt de vertaling gedefinieerd door een vector t (a, b), wat de verplaatsing van het initiële punt aangeeft. Het is te zeggen:

P (x, y) + t (a, b) = p '(x + a, y + b)

Als bijvoorbeeld op het coördinaatpunt P (8, -2) een vertaling T (-4, 7) wordt toegepast, wordt deze verkregen:

P (8, -2) + T (-4, 7) = P '[(8 + (-4)), ((-2) + 7)] = P' (4, 5)

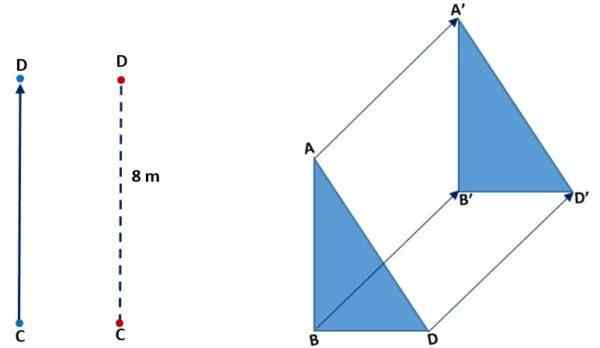
In de volgende afbeelding (links) kunt u zien hoe punt C is verplaatst om samen te vallen met de D. Hij deed het verticaal, de betekenis ging omhoog en de afstand of magnitude CD was 8 meter. In het rechterbeeld wordt de vertaling van een driehoek waargenomen:

Door rotatie

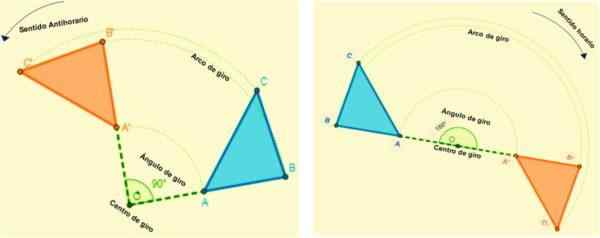
Zijn die isometrieën waarmee de figuur alle punten van een vlak kan draaien. Elk punt draait na een boog met een constante hoek en een vast punt (midden draaien) bepaald.

Dat wil zeggen, alle rotatie zal worden gedefinieerd door de rotatie en het draaien van de hoek in het midden. Wanneer een figuur wordt getransformeerd door rotatie, handhaaft deze de maat van zijn hoeken en zijkanten.

De rotatie treedt in een bepaalde richting op, het is positief wanneer de bocht anti -horair is (in tegenstelling tot hoe de klokken draaien) en negatief wanneer de beurt in de klok mee is.

Als een punt (x, y) wordt gedraaid ten opzichte van de oorsprong -dat is, is het rotatiecentrum (0,0) -, onder een hoek van 90^of 360^of De coördinaten van de punten zullen zijn:

Kan u van dienst zijn: statistische takken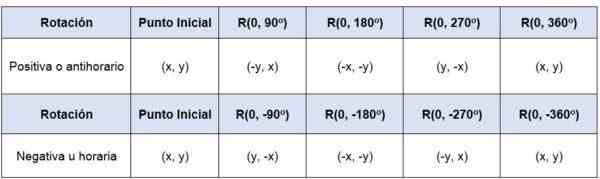

In het geval waarin de rotatie geen middelpunt heeft bij de oorsprong, moet de oorsprong van het coördinatensysteem naar de nieuwe gegeven oorsprong worden overgedragen, om de figuur te roteren met de oorsprong het midden.

Als bijvoorbeeld punt P (-5,2) een 90 rotatie wordt toegepast^of, Rond de oorsprong en in positieve zin zullen de nieuwe coördinaten zijn (-2,5).

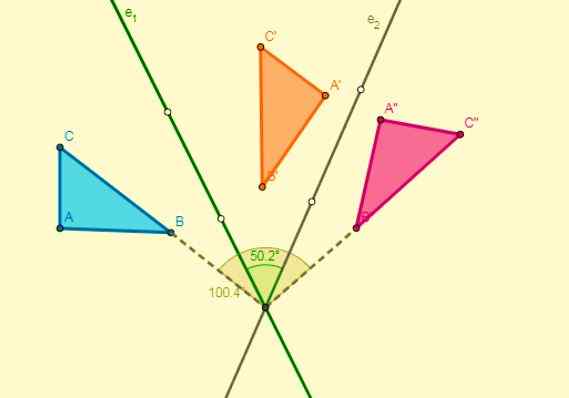
Door reflectie of symmetrie

Zijn die transformaties die de punten en cijfers van het vlak investeren. Deze investering kan met betrekking tot een punt zijn of kan ook zijn met betrekking tot een lijn.

Met andere woorden, in dit type transformatie is elk punt in de oorspronkelijke figuur geassocieerd met een ander punt (beeld) van de homologe figuur, zodat het punt en het beeld op dezelfde afstand zijn van een lijn genaamd Symmetry Axis.

Het linkerdeel van de figuur zal dus een weerspiegeling van de rechterkant zijn, zonder de vorm of de afmetingen te veranderen. De symmetrie transformeert een gelijke figuur maar omgekeerd, zoals te zien is in de volgende afbeelding:

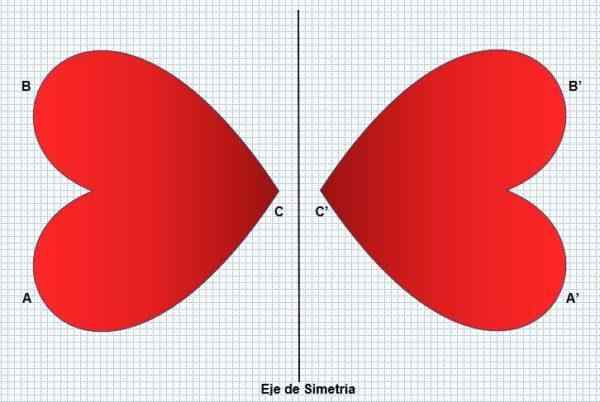
Symmetrie is aanwezig in veel aspecten, zoals sommige planten (zonnebloemen), dieren (pauw) en natuurlijke fenomenen (sneeuwvlokken). De mens weerspiegelt het in zijn gezicht, wat wordt beschouwd als een schoonheidsfactor. Reflectie of symmetrie kan van twee soorten zijn:

Centrale symmetrie

Het is die transformatie die optreedt ten opzichte van een punt, waarin de figuur zijn oriëntatie kan veranderen. Elk punt in de oorspronkelijke figuur en de afbeelding zijn op dezelfde afstand van een punt of, Symmetry Center genoemd. Symmetrie is centraal wanneer:

• Zowel het punt als het beeld en het midden behoren tot dezelfde lijn.
• Met een rotatie van 180^of van het midden of een figuur gelijk aan het origineel wordt verkregen.
• De slagen van de initiële figuur zijn parallel met de beroertes van de gevormde figuur.
• De betekenis van de figuur verandert niet, deze zal altijd in een schema zijn.

Kan u van dienst zijn: hoeveel moet u toevoegen aan 3/4 om 6/7 te krijgen?

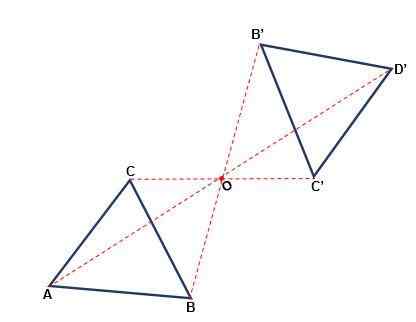Axiale symmetrie

Deze transformatie vindt plaats met betrekking tot de symmetrieas, waarbij elk punt in de initiële figuur is geassocieerd met een ander punt in de afbeelding en deze zijn op dezelfde afstand als de symmetrieas. De symmetrie is axiaal wanneer:

• Het segment dat zich bij een punt met zijn beeld verbindt, staat loodrecht op zijn symmetrieas.
• De cijfers veranderen hun betekenis met betrekking tot de richting van de beurt of de tijdrichting.
• Door de figuur te delen met een centrale lijn (symmetrieas), valt een van de resulterende helften volledig samen met een van de helften.

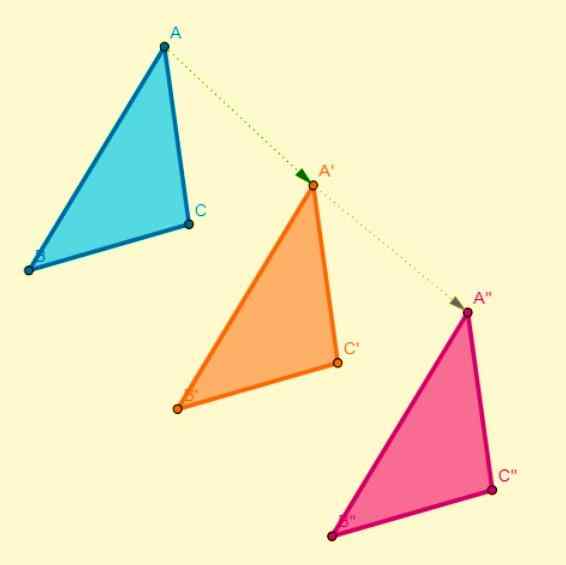
Samenstelling

Een isometrische transformatiescompositie verwijst naar de opeenvolgende toepassing van isometrische transformaties op dezelfde figuur.

Samenstelling van een vertaling

De samenstelling van twee vertalingen resulteert in een andere vertaling. Wanneer ze op het vlak worden uitgevoerd, blijven alleen de coördinaten van die as veranderen op het vlak, terwijl de coördinaten van de verticale as (y) hetzelfde blijven en vice versa.

Samenstelling van een rotatie

De samenstelling van twee beurten met hetzelfde centrum resulteert in een andere beurt, die hetzelfde centrum heeft en wiens amplitude de som zal zijn van de amplitudes van de twee beurten.

Als het midden van de bochten een ander centrum heeft, is de snede van de twee segmenten van vergelijkbare punten het centrum van rotatie.

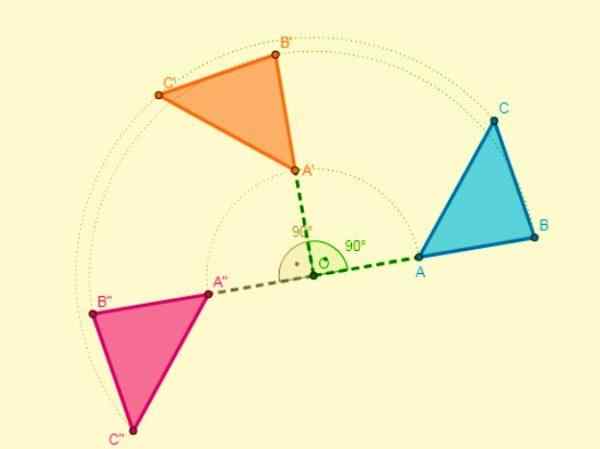
Samenstelling van symmetrie

In dit geval hangt de compositie af van hoe deze wordt toegepast:

• Als dezelfde symmetrie tweemaal wordt toegepast, is het resultaat een identiteit.
• Als twee symmetrieën worden toegepast met betrekking tot twee parallelle assen, wordt het resultaat vertaald en is hun verplaatsing twee keer de afstand van die assen:

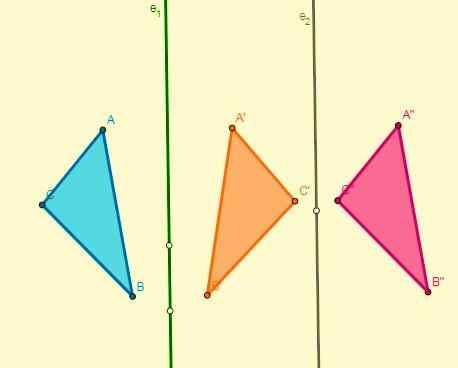
• Als twee symmetrieën worden toegepast ten opzichte van twee assen die worden gesneden op punt O (midden), wordt een rotatie met het midden verkregen en de hoek zal twee keer de hoek zijn die de assen vormen: