Mechanisch werk wat is, voorwaarden, voorbeelden, oefeningen

Hij mechanisch werk Het wordt gedefinieerd als de verandering in de energietoestand van een systeem, veroorzaakt door de werking van externe krachten zoals zwaartekracht of wrijving. De mechanische werkeenheden in het International System (SI) zijn Newton X Metro of Joules, afgekort door J.

Wiskundig wordt het gedefinieerd als het scalaire product van de krachtkracht door de vectorverplaatsing. Ja F Het is de constante kracht en l Het is de verplaatsing, beide vectoren, het werk W wordt uitgedrukt als: W = F ● l

Figuur 1. Terwijl de atleet het gewicht verhoogt, werkt hij wel tegen de zwaartekracht, maar wanneer hij het gewicht onbeweeglijk handhaaft, vanuit het oogpunt van de natuurkunde, doet hij dan geen werk. Bron: NeedPix.com

Wanneer de kracht niet constant is, moeten we het werk analyseren dat wordt gedaan wanneer de verplaatsingen erg klein of differentieel zijn. In dit geval, als het wordt beschouwd als een startpunt om punt A en als aankomst bij B te worden, wordt het totale werk verkregen door alle bijdragen aan hetzelfde toe te voegen. Dit komt overeen met het berekenen van de volgende integraal:

En zoals in het begin vermeld, op voorwaarde dat er een verandering in systeemergie is, zal dit zijn omdat er krachten uit het buitenland zijn die erop handelen, daarom:

Variatie in systeemergie = werk gedaan door externe krachten

ΔE = w_ext

Wanneer energie aan het systeem wordt toegevoegd, w> 0 en wanneer het wordt afgetrokken<0. Ahora bien, si ΔE = 0, puede significar que:

-Het systeem is geïsoleerd en er zijn geen externe krachten die erop werken.

-Er zijn externe krachten, maar ze doen geen werk aan het systeem.

Omdat de variatie in energie gelijkwaardig is aan het werk dat wordt uitgevoerd door externe krachten, is de eenheid als de energie ook de joule is. Dit omvat elk type energie: kinetisch, potentieel, thermisch, chemisch en meer.

[TOC]

Voorwaarden voor mechanisch werk

We hebben al gezien dat het werk wordt gedefinieerd als een scalair product. Laten we de definitie van het werk van constante kracht nemen en het concept van scalair product tussen twee vectoren toepassen:

W = F ● L = F.l.Cos θ

Waar F Het is de omvang van de kracht, l Het is de omvang van verplaatsing en θ Het is de hoek die bestaat tussen kracht en verplaatsing. In figuur 2 is er een voorbeeld van hellende externe kracht die op een blok (het systeem) werkt, dat een horizontale verplaatsing produceert.

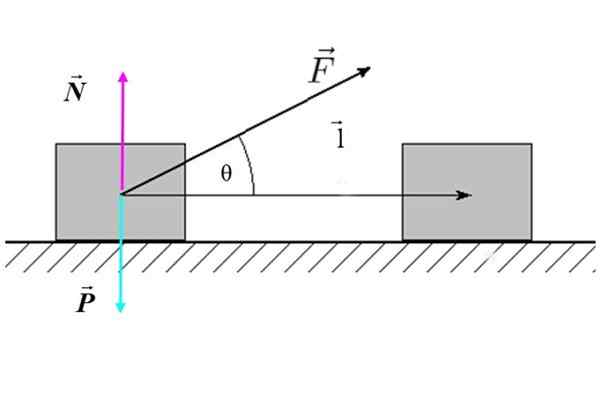Figuur 2. Vrij lichaamsdiagram van een blok dat op een plat oppervlak beweegt. Bron: f. Zapata.

Het werk herschrijven als volgt:

W = (f. cos θ). l

We kunnen bevestigen dat alleen het onderdeel van de kracht parallel aan de verplaatsing parallel is: F. cos θ es in staat om werk te doen. Als θ = 90º dan cos θ = 0 en het werk zou nietig zijn.

Daarom wordt geconcludeerd dat krachten loodrecht op verplaatsing geen mechanisch werk doen.

In het geval van figuur 2, noch de normale kracht N noch het gewicht P Ze werken wel, omdat beide loodrecht staan ​​op verplaatsing l.

De tekenen van werk

Zoals hierboven uitgelegd, W Het kan positief of negatief zijn. Wanneer cos θ> 0, Het werk dat met geweld wordt gedaan, is positief, omdat het dezelfde richting van de beweging heeft.

Het kan u van dienst zijn: Massalummer: wat is het en hoe u het kunt krijgen (met voorbeelden)

Ja cos θ = 1, Kracht en verplaatsing zijn parallel en het werk is maximaal.

In het geval cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.

Wanneer cos θ = -1, De kracht is volledig tegengesteld aan verplaatsing, zoals kinetische wrijving, wiens effect is om het object te stoppen waarop het werkt. Dus het werk is minimaal.

Dit komt overeen met wat er in het begin werd gezegd: als het werk positief is, wordt energie aan het systeem toegevoegd en als het negatief is, wordt het afgetrokken.

Netwerk W_netto Het wordt gedefinieerd als de som van de werken die worden gedaan door alle krachten die op het systeem werken:

W_netto = ∑W_Je

Dan kunnen we concluderen dat om het bestaan ​​van netto mechanisch werk te garanderen, het noodzakelijk is dat:

-Externe krachten werken op het object.

-Deze krachten staan ​​niet allemaal loodrecht op de verplaatsing (cos θ ≠ 0).

-De werken die door elke kracht zijn gedaan, worden niet met elkaar geannuleerd.

-Er is een verplaatsing.

Mechanische werkvoorbeelden

-Wanneer het nodig is om een ​​object in beweging te zetten op basis van rust, is het noodzakelijk om mechanisch werk te doen. Duw bijvoorbeeld een koelkast of een zware romp op een horizontaal oppervlak.

-Een ander voorbeeld van een situatie waarin het noodzakelijk is om mechanisch werk te doen, is om de snelheid van een bewegende bal te veranderen.

-Het is noodzakelijk om werk te doen om een ​​object op een bepaalde hoogte op de vloer op te heffen.

Nu zijn er even veel voorkomende situaties waarin Nee er wordt werk verricht, hoewel de verschijningen anders aangeven. We hebben gezegd dat we om een ​​object op een bepaalde hoogte op te heffen, we moeten werken, dus we laden het object, we brengen het boven ons hoofd op en houden het daar. Doen we werk?

Blijkbaar ja, want als het object zwaar is, worden de armen snel moe, maar hoeveel werk ook wordt gedaan, wordt er niet werk gedaan vanuit het oogpunt van de natuurkunde. Waarom niet? Omdat het object niet beweegt.

Een ander geval waarin het, ondanks een externe kracht, geen mechanisch werk verricht, is wanneer het deeltje een uniforme cirkelvormige beweging heeft.

Het kan u van dienst zijn: normale inspanning: waar het uit bestaat, hoe het wordt berekend, voorbeelden

Bijvoorbeeld een kind dat een steen draait die aan een touwtje is vastgebonden. De spanning van de snaar is de centripetale kracht die de rotatie van de steen mogelijk maakt. Maar te allen tijde staat deze kracht loodrecht op verplaatsing. Doe dan geen mechanisch werk, ondanks het feit dat het beweging bevordert.

De werk-energie-stelling Cinetics

De kinetische energie van het systeem is wat het heeft onder zijn beweging. Ja M is het deeg en v Het is de snelheid van beweging, kinetische energie wordt aangeduid door K En het wordt gegeven door:

K = ½ mV²

Per definitie kan de kinetische energie van een object niet negatief zijn, omdat zowel de massa als het kwadraat van de snelheid altijd positieve hoeveelheden zijn. Kinetische energie kan 0 zijn, wanneer het object in rust is.

Om de kinetische energie van een systeem te veranderen, is het noodzakelijk-. Hiervoor is het noodzakelijk om netto werk aan het systeem te doen, daarom:

W_netto = ΔK

Dit is de stelling van het werk - kinetische energie. Zegt dat:

Netto -werk is gelijk aan de verandering in de kinetische energie van het systeem

Merk op dat hoewel K altijd positief is, AK positief of negatief kan zijn, omdat:

ΔK = k_laatste - K _voorletter

Ja K_laatste >K _voorletter Het systeem heeft energie gewonnen en ΔK> 0. Integendeel, ja K_laatste < K _voorletter, Het systeem heeft energie opgeleverd.

Werk gedaan om een ​​lente uit te rekken

Bij het uitrekken (of comprimeren) van een veer is het noodzakelijk om een ​​werk te doen. Dit werk wordt in het voorjaar opgeslagen, waardoor dit op zijn beurt kan werken aan bijvoorbeeld een blok dat aan een van de uiteinden is bevestigd.

De wet van Hooke stelt dat de kracht die door een veer wordt uitgeoefend, een restitutieteem is - het is in strijd met verplaatsing - en ook evenredig met die verplaatsing. De evenredigheidsconstante hangt af van hoe de veer is: zacht en gemakkelijk vervormbaar of rigide.

Deze kracht wordt gegeven door:

F_R = -kx

In de uitdrukking, F_R Het is de kracht, k Het is de veerconstante en X Het is de verplaatsing. Het negatieve teken geeft aan dat de kracht die door de veer wordt uitgeoefend zich verzet tegen verplaatsing.

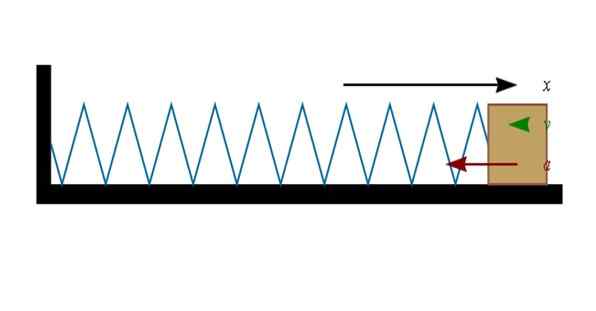figuur 3. Een gecomprimeerde of uitgerekte veer werkt op een object dat aan het einde is gebonden. Bron: Wikimedia Commons.

Als de veer wordt gecomprimeerd (links in de figuur), zal het blok aan het uiteinde naar rechts gaan. En wanneer de veer is uitgerekt (rechts), wil het blok naar links bewegen.

Om de veer te comprimeren of te strekken, moet een externe agent het werk doen, en omdat het een variabele kracht is, om dit werk te berekenen, moet u de definitie gebruiken die in het begin is opgetreden:

Kan u van dienst zijn: Darcy Law

Het is heel belangrijk op te merken dat dit het werk is dat door de externe agent is gedaan (bijvoorbeeld de hand van een persoon) om de veer te comprimeren of te strekken. Daarom verschijnt het negatieve teken niet. En omdat posities vierkant zijn, ongeacht of ze compressies of verlengingen zijn.

Het werk dat de lente op zijn beurt op het blok zal doen, is:

W_lente = -W_ext

Opdrachten

Oefening 1

Het blok in figuur 4 heeft massa M = 2 kg en glijdt zonder wrijving door het hellende vlak, met α = 36.9e. Ervan uitgaande dat het vanaf de bovenkant van het vlak uit de rest mag glippen, waarvan de hoogte h = 3 m is, vindt u de snelheid waarmee het blok de basis van het vlak bereikt, door de kinetische kinetische kinetische werking.

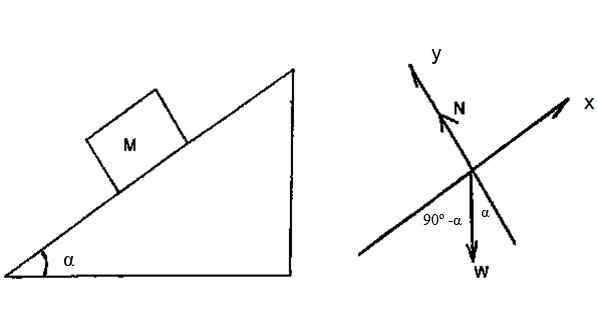Figuur 4. Een blok glijdt naar beneden op een hellend vlak zonder te wrijven. Bron: f. Zapata.

Oplossing

Het vrije lichaamsdiagram laat zien dat de enige kracht die in staat is om op het blok te werken, het gewicht is. Nauwkeuriger: de gewichtscomponent langs de X -as.

De afstand die door het blok op het vlak wordt afgelegd, wordt berekend door trigonometrie:

D = 3 / (cos 36.9º) M = 3.75 m

W_gewicht = (Mg). D. cos (90-a) = 2 x 9.8 x 3.75 x cos 53.1e j = 44.1 J

Door kinetische kinetische stelling te werken:

W_netto = ΔK

W_netto = W_gewicht

ΔK = ½ mV_F²- ½ mV_of²

Omdat het uit rust is vrijgegeven, v_of = 0, daarom:

W_netto = ½ mv_F²

Oefening 2

Een horizontale veer, waarvan de constante k = 750 n/m is, wordt aan één uiteinde aan een muur bevestigd. De ene persoon comprimeert het andere uiteinde op een afstand van 5 cm. Bereken: a) de kracht die door de persoon wordt uitgeoefend, b) het werk dat hij deed om de veer te comprimeren.

Oplossing

a) De grootte van de door de persoon uitgeoefende kracht is:

F = kx = 750 n/ m . 5 x 10 ^-2 M = 37.5 n.

b) Als het lente -uiteinde oorspronkelijk in x staat₁ = 0, om het van daar naar de eindpositie te brengen x₂ = 5 cm, het is noodzakelijk om het volgende werk te doen, volgens het resultaat verkregen in de voorgaande sectie:

W_ext = ½ K (x₂² - X₁²) = 0.5 x 750 x (0.05² -0²) J = 0.9375 J.

Referenties

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 2. Dynamisch. Uitgegeven door Douglas Figueroa (USB).
2. Iparraguirre, l. 2009. Basismechanica. Collectie en wiskunde van natuurwetenschappen. Gratis online distributie.
3. Ridder, r. 2017. Fysica voor wetenschappers en engineering: een strategiebenadering. Pearson.
4. Physics Libhethexts. Werk-energie-stelling. Hersteld van: Phys.Librhetxts.borg
5. Werk en energie. Hersteld van: natuurkunde.Bu.Edu
6. Werk, energie en kracht. Hersteld van: ncert.Nek.in