Horizontale schietfuncties, formules en vergelijkingen, oefeningen

Hij Horizontaal schieten Het is de lancering van een projectiel met horizontale snelheid van een bepaalde hoogte en overgelaten aan de actie van de zwaartekracht. Zonder rekening te houden met de weerstand van de lucht, heeft het door de mobiel beschreven traject de vorm van een paraboolboog.

Horizontaal objecten projecteren is vrij gebruikelijk. De projectielen worden met allerlei uiteinden gegooid: van de stenen waarmee de dammen aan het begin van het verhaal werden neerslachtig, tot degenen die worden uitgevoerd in balsporten en op de voet worden gevolgd door drukte.

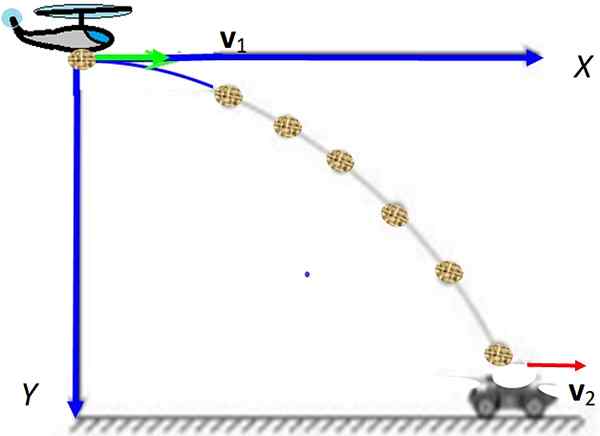
Figuur 1. Horizontaal schieten met rode snelheidscomponenten. Merk op dat de horizontale component constant blijft terwijl verticaal groeit. Bron: Wikimedia Commons.

[TOC]

Kenmerken

De belangrijkste kenmerken van de horizontale schieten zijn:

-De initiële snelheid die aan het projectiel wordt verstrekt, staat loodrecht op de zwaartekracht.

-De beweging vindt plaats in een vliegtuig, dus er zijn twee coördinaten nodig: X En En.

-Het wordt gedaan vanaf een bepaalde hoogte h boven het maaiveld.

-De tijd dat het projectiel in de lucht duurt, wordt gebeld vluchttijd.

-Factoren zoals luchtweerstand of schommelingen worden niet in aanmerking genomen bij de waarde van G.

-De vorm, grootte en massa van het projectiel hebben geen invloed op de beweging.

-De beweging ontleedt in twee gelijktijdige bewegingen: één verticaal naar beneden onder de actie van G; De andere, horizontaal, met constante snelheid.

Formules en vergelijkingen

Cinematische vergelijkingen voor horizontale lancering worden verkregen uit de vergelijkingen voor vrije val en die van de uniforme rechtlijnige beweging.

Kan u van dienst zijn: interne energie

Zoals animatie duidelijk wordt weergegeven in figuur 1, wordt het projectiel voorzien van een horizontale initiële snelheid, aangeduid als v_of = V_os Je (De vetgedrukte in gedrukte tekst geeft aan dat het een vector is).

Opgemerkt wordt dat de initiële snelheid de omvang heeft v_os en wordt geleid langs de as X, Wat is de richting van de eenheidsvector Je. In de animatie wordt ook gewaarschuwd dat de initiële snelheid geen verticale component heeft, maar terwijl deze valt, neemt deze component uniform toe, dankzij de actie van G, Gravity Acceleration.

Wat betreft de horizontale component van snelheid, deze blijft constant terwijl de beweging duurt.

Volgens wat er is gezegd, worden posities vastgesteld als een functie van de tijd, zowel op de horizontale as als in de verticale as. Het recht wordt genomen als +x -as, terwijl het adres omlaag is -en en. De waarde van de zwaartekracht is G = -9.8 m/s² of -32 voet/s²:

x (t) = x_of + v_os.t (horizontale positie); v_os het is constant

en (t) = y_of + v_Oy.T - ½ g.T² (verticale positie); v_En = V_Oy - G.T (verticale snelheid)

Positie, snelheid, vliegtijd en maximaal horizontaal bereik

De vergelijkingen zijn vereenvoudigd als ze de volgende beginposities kiezen: X_of = 0, En_of = 0 op de plaats van de lancering. Daarnaast v_Oy = 0, Omdat de mobiel horizontaal wordt geprojecteerd. Met deze keuze zijn de bewegingsvergelijkingen zo:

x (t) = V_os.T; v_X = V_os

en (t) = - ½ g.T²; v_En = - g.T

Wanneer de tijd niet beschikbaar is, is de vergelijking die snelheden en verplaatsingen relateert, nuttig. Dit is geldig voor verticale snelheid, omdat de horizontale gedurende de beweging constant blijft:

Kan u bedienen: calciumfluoride (CAF2): structuur, eigenschappen, gebruik

v_En² = V_Oy² + 2.G .y = 2.G.En

Vluchttijd

Om de Vliegtijd t_vlucht, Stel dat de mobiel van een hoogte wordt geprojecteerd H op de vloer. Aangezien de oorsprong van het referentiesysteem op het lanceringspunt is gekozen, is deze in positie wanneer het de grond bereikt -H. Dit vervangen in vergelijking 2) Het wordt verkregen:

-H = - ½ g.T²_vlucht

T_vlucht = (2H/g)^½

Maximaal bereik

Hij Horizontaal bereik Deze tijd wordt verkregen door te vervangen x (t):

X_Maximaal = V_os. (2h/g)^½

Opgeloste oefeningen

-Oefening opgelost 1

Een helikopter vliegt horizontaal en handhaaft een constante hoogte van 580 m wanneer deze een doos met voedsel op een vluchtelingenkamp vrijgeeft. De doos landt op een horizontale afstand van 150 m vanaf het punt van de lancering. Zoek: a) De vliegtijd van de doos.

b) De snelheid van de helikopter.

c) Hoe snel de doos raakte?

Oplossing

a) De hoogte h waaruit het voedsel wordt vrijgegeven, is h = 500 m. Met deze gegevens bij het vervangen krijgt u:

T_vlucht = (2H/g)^½= (2 x 580/9.8) ^½S = 10.9 s

b) De helikopter draagt ​​de horizontale initiële snelheid v_os van het pakket en omdat een van de gegevens is X_maximaal:

X_Maximaal = V_os. (2h/g)^½ ® v_os = x_Maximaal /(2H/g)^½= x_Maximaal / T_vlucht = 150 m/ 10.9 s = 13.8 m/s

c) De snelheid van het projectiel op elk moment is:

v_En = -g.T = -9.8 m/ s² x 10.9 s = -106.82 m/s = - 384.6 km/h

Het negatieve teken geeft aan dat de mobiel naar beneden gaat.

-Oefening opgelost 2

Van een vlak dat horizontaal op een hoogte vliegt H = 500 m En 200 km/h Een pakket valt dat moet vallen op een open voertuig dat naar marcheert 18 km/h op de weg. In welke positie moet het vliegtuig het pakket in het voertuig laten vallen? Houd geen rekening met luchtweerstand of windsnelheid.

Kan u van dienst zijn: dimensionale analyseFiguur 2. Schema voor de oefening opgelost 2. Bron: voorbereid door F. Zapata.

Oplossing

Het is handig om alle eenheden voor het eerst aan het internationale systeem te geven:

18 km/h = 6 m/s

200 km /h = 55 m /s

Er zijn twee mobiele telefoons: vlak (1) en voertuig (2) en het is noodzakelijk om een ​​coördinatensysteem te kiezen om ze beide te vinden. Het is handig om dit te doen op het startpunt van het pakket in het vliegtuig. Het pakket wordt horizontaal geprojecteerd met de snelheid die het vliegtuig draagt: v₁, Terwijl het voertuig naar v₂ veronderstelde constante.

-Vliegtuig

Initiële positie: x = 0; y = 0

Initiële snelheid = v₁ (horizontaal)

Positievergelijkingen: en (t) = -½G.T²  ; x (t) = V₁.T

-Voertuig

Eerste positie: x = 0, y = -h

Initiële snelheid = v₂  (constante)

x (t) = x_of + v₂. T

De tijd dat de pakketvlucht duurt, is:

T_vlucht = (2H/g)^½ = (2 × 500/9.8)^½S = 10.1 s

Op dit moment heeft het pakket een horizontale verplaatsing van:

X_Maximaal = V_os . (2h/g)^½= 55 m/s x 10.1 s = 556 m.

Op dit moment is het voertuig ook horizontaal verplaatst:

x (t) = V₁.T = 6 m/s x10.1 s = 60.6 m

Als het vliegtuig het pakket onmiddellijk vrijgeeft dat het voertuig eronder doorstort, zal het er niet in staat zijn om er recht in te vallen. Om dat te laten gebeuren, moet hij het teruggooien:

D = 556 m - 60.6 m = 495.4 m.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill. 74-84.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).117 - 164.
3. Projectielbeweging. Hersteld van: Phys.Librhetxts.borg.
4. Rex, a. 2011. Fundamentals of Physics. Pearson. 53-58.
5. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. McGraw Hill. 126-131.