Soorten driehoeken

Classificatie van driehoeken

Een driehoek is een polygoon of geometrische figuur met drie zijden, drie hoekpunten en drie hoeken. De zijkanten zijn elk van de rechte lijnen die het vormen. De hoekpunten zijn de punten waar de zijkanten worden samengevoegd; De hoeken zijn de bogen of openingen die in de buurt van de hoekpunten worden gevormd, door twee kanten samen te voegen.

Een driehoek kan ook worden gedefinieerd als het gebied bepaald door drie lijnen. De som van zijn drie hoeken is altijd gelijk aan 180º. De lengte van een van zijn zijden is altijd minder dan het resultaat van de som van de lengte van de andere twee zijden, maar groter dan de aftrekking.

Driehoeken zijn de eenvoudigste geometrische figuren en dienen om de wiskundige eigenschappen van andere meer complexe figuren, zoals pentagons of zeshoeken te onderzoeken.

Ze worden ook gebruikt in andere wetenschappen, zoals topografie, navigatie of astronomie. In het laatste worden ze gebruikt om de afstand te kennen die ons scheidt van een verre lichtblauw lichaam van twee observatiepunten op de aarde. Deze methode staat bekend als parallage.

De driehoeken worden geclassificeerd volgens de lengte van hun zijden of volgens de amplitude van hun hoeken.

Soorten driehoeken volgens hun partijen

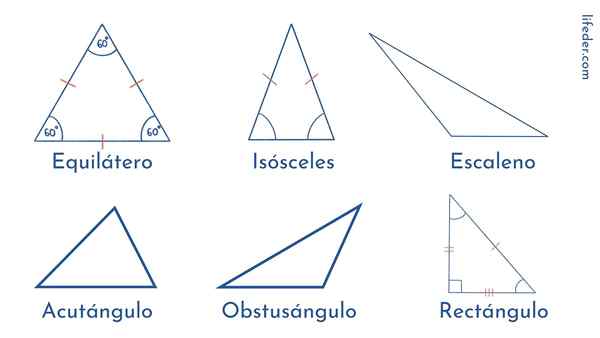
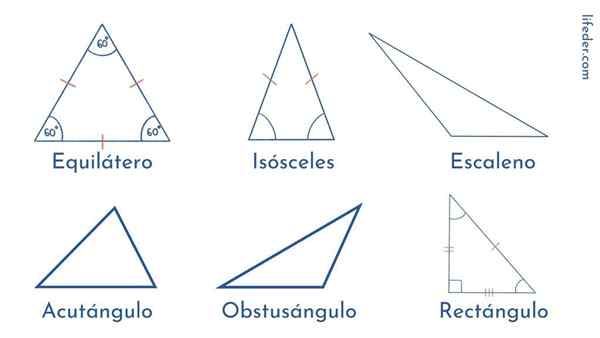
Gelijkzijdige driehoek

De zijkanten van dit type driehoek hebben exact dezelfde lengte. En hetzelfde geldt voor hun hoeken: de drie meet 60º. Daarom zeggen we dat de gelijkzijdige driehoek een gewone polygoon is.

Ongelijkbenige driehoek

In tegenstelling tot de gelijkzijdige, is alles in de scaleense driehoek ongelijk: de drie zijden hebben verschillende lengtes en verschillen de hoeken in amplitude.

Kan u van dienst zijn: gecombineerde bewerkingen

Gelijkbenige driehoek

In dit type driehoek zien we dat twee kanten dezelfde maat hebben, terwijl de resterende zijde anders is. Hetzelfde wordt waargenomen in de amplitude van de hoeken: twee zijn hetzelfde en een ander.

Soorten driehoeken volgens hun hoeken

Rechter driehoek

Het wordt gekenmerkt door een rechte hoek te hebben, dat wil zeggen 90º. Zijn andere twee hoeken zijn acuut of minder dan 90º.

In dit type driehoeken wordt de langste zijde hypotenusa genoemd, terwijl nog een twee kanten de categorieën zijn.

Schuine driehoek

Driehoeken met geen enkele rechthoek behoren tot dit type. Ze zijn onderverdeeld in twee soorten:

Acutangle -driehoek: Zijn drie hoeken zijn acuut.

Stompe driehoek: Ze hebben twee acute hoeken en één stompe of groter dan 90º.

Gemengde driehoeken

Dezelfde driehoek kan worden geclassificeerd volgens de twee criteria, dat wil zeggen volgens de lengte van hun zijkanten en de amplitude van hun hoeken.

Een rechthoekige driehoek kan bijvoorbeeld ook escalano of gelijkbenig zijn, maar het kan niet gelijkwaardig zijn, omdat deze laatste geen rechte hoek presenteert.

Een gelijkzijdige driehoek kan echter acuut zijn, omdat deze effectief drie acute of minder dan 90º hoeken heeft.

Scalene stompe driehoek

Een scaleense driehoek kan stompe zijn, omdat zowel de amplitude van zijn hoeken als de lengte van de zijkanten verschillend zijn.

Hoe de omtrek van een driehoek te berekenen?

Het product van de som van de lengte van de drie zijden van een driehoek wordt perimeter genoemd.

Laten we eens kijken naar enkele voorbeelden.

1- We worden gevraagd om de omtrek te vinden van een scaleense driehoek waarvan de zijkanten 6, 8 en 4 centimeter. Het enige dat we moeten doen is toevoegen:

Kan u van dienst zijn: absolute constante

6 + 8 + 4 = 18

Daarom is de omtrek van deze scaleene driehoek 10 centimeter.

2- Dan vragen ze ons om de omtrek van een gelijkbenige driehoek te berekenen waarvan de zijkanten 4 centimeter de twee en 6 centimeter de resterende zijde meten. Aangezien twee van de zijden dezelfde lengte hebben, moeten we hetzelfde cijfer twee keer plaatsen, zoals deze:

4 + 4 + 6 = 14

De omtrek van deze driehoek is 14 centimeter.

3- Een laatste voorbeeld. We hebben de taak om de omtrek van een gelijkzijdige driehoek van 9 centimeter zijwaarts te bepalen. Zoals we weten dat de kenmerken van de verschillende soorten driehoeken, weten we dat het gelijkzijdige wordt onderscheiden omdat de drie kanten gelijk zijn. Daarom:

9 + 9 + 9 = 27

De omtrek van dit gelijkzijdige is 27 centimeter.

Mediatrices, bisectors en medium

Dit zijn de drie soorten rechte lijnen die in een driehoek kunnen worden getrokken.

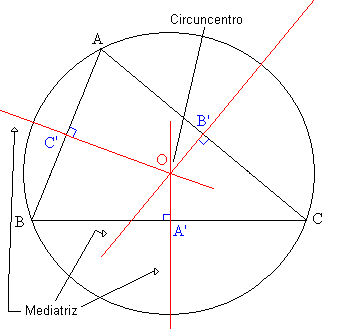
Mediatrices

Er zijn drie, één aan elke kant van de driehoek. De MediaTrix is ​​een rechte lijn die door het middelpunt van de driehoekige kant gaat waarmee hij overeenkomt. De drie mediatrices van een driehoek kruisen elkaar op een punt dat bekend staat als CircumCentro, dat zich op dezelfde afstand bevindt van elk van de hoekpunten van de driehoek.

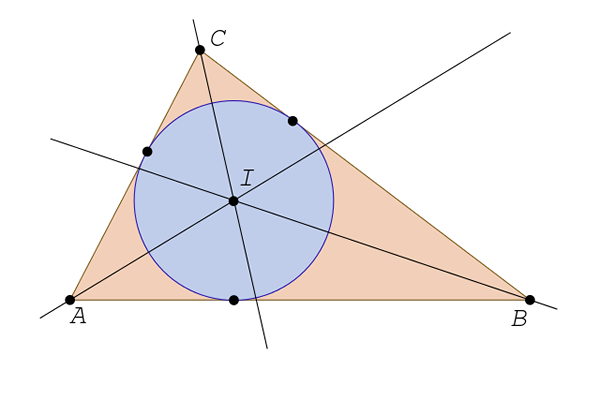
Bissectoren

Er zijn er drie, één voor elke hoek. De bissector is een rechte lijn die begint bij het hoekpunt en de hoek verdeelt in twee gelijke delen. De bissectoren van een driehoek kruisen elkaar op een punt dat bekend staat als st incenter.

Medium

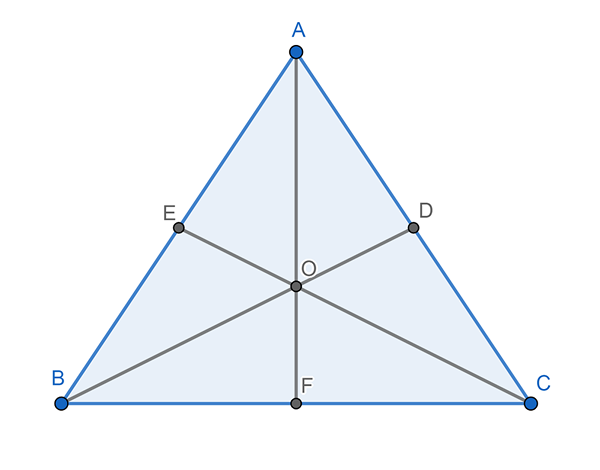
Er zijn ook drie, één voor elk hoekpunt. Een mediaan is een lijn die begint bij een hoekpunt en het middelpunt aan de andere kant bereikt. De mediaan van een driehoek kruisen elkaar op een punt genaamd Baricentro.

Kan u van dienst zijn: bemonsteringsfout: formules en vergelijkingen, berekening, voorbeelden

De afstand tussen een van de drie hoekpunten en het barycenter is gelijk aan tweederde (2/3) van de totale lengte van de overeenkomstige mediaan. Als het mediane CE bijvoorbeeld 5 centimeter meet, is de afstand tussen C en de baricenter (O) gelijk 5 x 2/3, of wat hetzelfde is, 5 x 0,66, wat resulteert in 3, 3 centimeter.

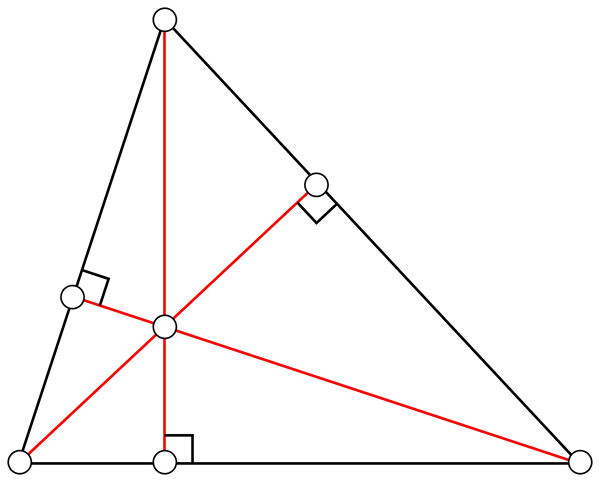
Hoogtes

Het is een rechte lijn die met de andere kant bij een hoekpunt komt. De drie hoogten van een driehoek kruisen elkaar op een punt dat Ortotroeterer wordt genoemd. Afhankelijk van het type driehoek kan het orthocentrum zich binnen of buiten het driehoekgebied bevinden.

Hoe het driehoeksgebied te berekenen?

Het gebied van een driehoek van welke aard dan ook kan bekend zijn bij het toepassen van de volgende formule:

A = B X H / 2

In deze vergelijking verwijst A naar het gebied; B verwijst naar de basis en H is de hoogte.

Laten we eens kijken naar een voorbeeld. We worden gevraagd om het gebied van een driehoek te berekenen waarvan de basis 12 centimeter meet en waarvan de hoogte 7 centimeter is. We hebben dus:

B = 12

H = 7

We passen de formule toe:

A = 12 x 7/2

A = 84/2

A = 44

Deze driehoek heeft daarom een ​​oppervlakte van 44 vierkante centimeter.