Tetradecágono

Wat is een tetradecágono?

De Tetradecágono is een platte en gesloten geometrische figuur van 14 zijden, behorend tot de Polygons -familie. Het is ook bekend onder de naam van Tetrakaidecágono, Alle woorden afgeleid van Griekse woorden: "tetra" (cuatri), "kai" (meer), "verval" (tien) en "gon" (hoek), omdat het ook 14 binnenhoeken heeft.

De figuur toont een reguliere tetradenon, dat wil zeggen een wiens zijden en interne hoeken hebben allemaal dezelfde maatregel, die de hoofdkenmerken van deze figuur toont.

Figuur 1.- Regelmatige tetrade met zijn belangrijkste kenmerken. Bron: f. Zapata.

Tetradecágono -elementen

• Zijkanten: Ze worden de 14 -lijnsegmenten genoemd die zijn gesloten om de figuur te vormen. Ze kunnen allemaal dezelfde lengte hebben, in welk geval de polygoon regelmatig is, of ze kunnen anders zijn en dan is er een onregelmatige tetrade.
• Hoekpunten: Ze zijn de snijpunten tussen opeenvolgende segmenten en de Tetradecágono heeft 14 hoekpunten.
• Centrum: Opeenvolgend punt van de hoekpunten.
• Radio: segment dat het centrum verenigt met een hoekpunt.
• Interne hoek: Het wordt gevormd door de binnenkant van de figuur en tussen twee opeenvolgende of aangrenzende segmenten. Meet 154.286º voor de reguliere Tetradecágon, ongeacht de grootte van de zijkant.
• Externe hoek: gevormd tussen één kant en de verlenging van een van de aangrenzende zijden. Ongeacht de zijlengte, deze hoek meet 25.7143º voor een gewone tetrade.
• Centrale hoek: Degene met zijn hoekpunt dat samenvalt met het midden van de polygoon en zijn zijkanten zijn twee opeenvolgende radio's.
• Diagonaal: segment dat twee niet -opeenvolgende hoekpunten verbindt.

Hoe is een tetradecágono?

De reguliere polygonen van N -zijden die zijn gebouwd met regel en kompas hebben een N van de vorm 2^R P₁… P_k, zijn P_Je Fermat Primo -getallen verschillend, en op zijn beurt de priemgetallen van Fermat krijgen vorm 2^N + 1.

Kan u van dienst zijn: in afwachting van een lijn: formule en vergelijkingen, representatie, voorbeelden

De tetradecágono heeft n = 14 zijden, maar 14 = 7 × 2, die geen fermat neven zijn, omdat ze niet op de aangegeven manier kunnen worden uitgedrukt. Daarom geeft deze polygoon geen exacte constructie toe met regel en kompas, maar een constructie die zeer goed nadert, via verschillende methoden.

Algemene methode om regelmatige polygonen te bouwen

Het volgende is een algemene methode (niet de enige) om regelmatige polygonen te bouwen die in een omtrek zijn geregistreerd, inclusief de reguliere tetrade.

Het bestaat uit het delen van de verticale diameter van deze omtrek in zoveel gelijke delen als zijkanten heeft de polygoon om te tekenen. In het geval van Tetradecágono zullen ze de 14 delen zijn genummerd in afbeelding 2. Dit zijn de stappen:

• Teken een verticale diameter van A tot B.
• Teken vervolgens een semi -recht vanaf punt A, open het kompas met een willekeurige opening en maak er 14 gelijk verdeeld verdeeldheid erover. Semirrect en zijn divisies kunnen uit de omtrek komen.
• Word lid van het 14va -merk (in blauw in de afbeelding) aan het einde van de semi -rechtse met punt B.
• Om door te gaan met de rest van de tekens in de semi -recreatie met de respectieve punten op de verticale diameter (groene punten).
• Met de punt van het kompas in a en opening gelijk aan de maat van de diameter van de omtrek is een boog getrokken. Met dezelfde maatregel, maar het ondersteunen van de punt in B (punt 14 van figuur 2) is een andere boog getrokken, die wordt gesneden met de eerste op punten v en v 'aangegeven.

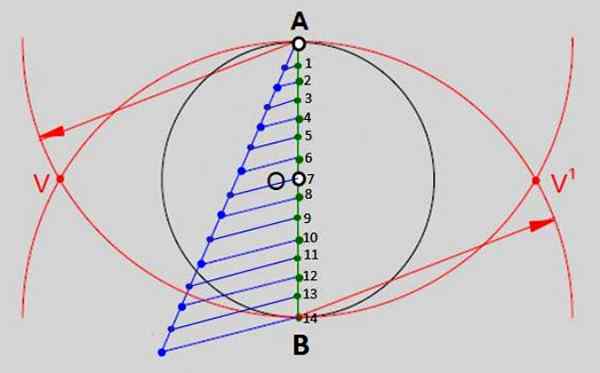Figuur 2.- Een van de algemene methoden om regelmatige polygonen te bouwen, is het verdelen van de diameter van de omtrek in zoveel gelijke delen als zijkanten de polygoon heeft. In het geval van reguliere tetradech zijn er 14 gelijke delen. Bron: f. Zapata.

• Trek nu met de regel een lijn van v 'naar punt 2 en verleng deze om de omtrek te kruisen op punt C van figuur 3. Markeer het snijpunt, dat een van de hoekpunten van de figuur zal zijn.

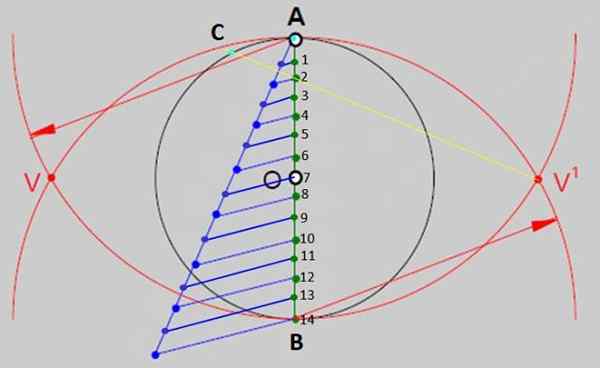Kan u van dienst zijn: statistische takken figuur 3.- Het AC -segment is de maat van de zijkanten van de gebouwde tetradecion. Bron: f. Zapata.

• Open het kompas in de AC -afstand en het ondersteunen van de punt in A of C, die bogen van gelijke maatregel over de gehele omtrek tekenen, op deze manier is het verdeeld in ongeveer gelijke delen, de kruispunten tussen de bogen en de omtrek zijn de hoekpunten zijn de hoek hoekpunten van Tetradecágono.
• Voeg met een regel toe met de hoekpunten met lijnsegmenten en vormt de zijkanten van de polygoon.
• Wis zorgvuldig hulpconstructies.

In de volgende animatie wordt een andere benaderingmethode getoond, met regel en kompas:

Figuur 4.- Animatie die laat zien hoe een tetradecágon wordt gemaakt (ongeveer gewone polygoon). Bron: Wikimedia Commons.

Formules voor gewone tetrade

De volgende formules zijn geldig voor reguliere polygonen:

• Bladnummer: n
• Zijmaat: a
• Apothem: L_NAAR
• Radio: r
• Perimeter: P
• Gebied: a
• Interne hoek: ik
• Externe hoek: e
• Diagonaal: D

Bekende kant van de apothem

A = 2L_NAAR × tg (π/n)

Voor n = 14:

A = 2L_NAAR × tg (π/14)

Bekende kant de radio

A = 2R × Sen (π/n)

Ja n = 14:

A = 2R × Sen (π/14)

Bekende perimeter de zijkant

De omtrek is de som van de zijkanten. Wanneer de Tetradecágono regelmatig is:

P = n⋅a = 14⋅A

Als de tetradecágono onregelmatig is, moeten alle zijden rechtstreeks worden toegevoegd om de perimeter te verkrijgen.

Bekend gebied de zijkant

A = ¼ na² × COT (π/n)

Voor n = 14:

A = ¼ (14e²) × COT (π/14) = (7/2) a² × COT (π/14)

Bekend gebied

A = n⋅l_NAAR ² × tg (π/n)

N = 14 resultaten nemen:

A = 14l_NAAR ² × tg (π/14)

Gebied gebaseerd op de perimeter en apothem

A = (P × L_NAAR)/2

Kan u van dienst zijn: Bayes Stelling

Binnenhoekmaatregel

 Wanneer n = 14, meet de interne hoek van de tetradecágono in graden:

I = 12 × 180º /14 = 154.286º

Externe hoekmeting

E = 360º/n

Wanneer n = 14 u hebt:

E = 25.7143º

Diagonalen

De formule voor het berekenen van het aantal diagonalen aanwezig in een polygoon, regelmatig of niet, is:

Voor n = 14:

D = 14 × 11/2 = 77 diagonalen

Voorbeelden

Een ander voorbeeld van Tetradecágon

Regelmatige polygonen verschijnen herhaaldelijk in tal van ontwerpen, zoals valuta. In het geval van reguliere Tetradenon verschijnt dit in Maleisische herdenkingsmunten, die zijn partijen vertegenwoordigen aan elk van de veertien geconfedereerde staten van die natie.

Concave en convex tetradecágonos

Over het algemeen kunnen polygonen zoals Tetradecágono convex of concaaf zijn, in het eerste geval is de maat van hun interne hoeken niet groter dan 180º. De reguliere tetradech is convex, zoals elke reguliere polygoon, omdat een van zijn interne hoeken 154 meet.286º.

Aan de andere kant, in de concave tetradech, meet een of meer van zijn interne hoeken meer dan 180º.

Numeriek voorbeeld

Gegeven een normale TetraDagon waarvan de zijde 5 cm meet, zoek:

a) perimeter
b) Apotheme -meting
c) Radiolengte
d) gebied

Antwoorden

a) Omdat het een gewone polygoon is, is de omtrek:

P = 14 × 5 cm = 70 cm.

b) Uit vergelijking A = 2l_NAAR × tg (π/14), waarbij a = 5 cm, de apothem l_NAAR:

L_NAAR = a / [2 × tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

c) Radio R kan worden berekend door A = 2R × Sen (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Er zijn verschillende alternatieven voor het gebied, bijvoorbeeld a = (p × l_NAAR)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Arturo -geometrie. Algemene methode voor het tekenen van polygonen die zijn ingeschreven in omtrek. Hersteld van YouTube.com
3. Soepcalculator. Regelmatige polygooncalculator. Hersteld van: calculatorosoup.com.
4. Tekening. Regelmatige polygonen. Hersteld van: tekenen.com.
5. Eisen, b. Concave polygoon. Hersteld van: UniversOFormulas.com.
6. Wikipedia. Bouwbare polygoon. Hersteld van: is.Wikipedia.borg.