Newton's Third Law -aanvragen, experimenten en oefeningen

De De derde wet van Newton, ook wel genoemd Wet van actie en reactie Hij bevestigt dat wanneer een object sterkte over een ander uitoefent, deze laatste ook uitoefent op de eerste een kracht van gelijke grootte en richting en tegenovergestelde zin.

Isaac Newton bracht zijn drie wetten uit in 1686 in zijn boek Philosophiae Naturalis Principia Mathematica of wiskundige principes van natuurlijke filosofie.

Een ruimteraket ontvangt de nodige voortstuwing dankzij de uitgezette gassen. Bron: Pixabay.

[TOC]

Verklaring en formules

De wiskundige formulering van de derde wet van Newton is heel eenvoudig:

F₁₂ = -F_eenentwintig

Een van de krachten wordt genoemd actie En de andere is de reactie. Het is echter noodzakelijk om het belang van dit detail te benadrukken: beide handelen op verschillende objecten. Ze doen het ook tegelijkertijd, hoewel deze terminologie ten onrechte suggereert dat de actie plaatsvindt vóór en de reactie daarna.

Omdat krachten vectoren zijn, worden ze met vet aangeven. Deze vergelijking geeft aan dat er twee objecten zijn: Object 1 en Object 1 en. De kracht F₁₂ Het is degene die object 1 uitoefent op object 2. De kracht F_eenentwintig wordt uitgeoefend door Object 2 op object 1. En het teken (-) wijst erop dat ze tegen zijn.

Bij het zorgvuldig observeren van de derde wet van Newton is er een belangrijk verschil met de eerste twee: terwijl ze een enkel object oproepen, verwijst de derde wet naar twee verschillende objecten.

En als u goed nadenkt, vereisen interacties paren van objecten.

Dat is de reden waarom de krachten van werking en reactie niet worden geannuleerd of in evenwicht, hoewel ze dezelfde omvang en richting hebben, maar verder: ze worden in verschillende lichamen toegepast.

Toepassingen

Ballinteractie - Aarde

Hier is een zeer dagelijkse toepassing van een interactie met betrekking tot de derde wet van Newton: een bal die verticaal en de aarde valt. De bal valt op de grond omdat de aarde een aantrekkingskracht uitoefent, die bekend staat als zwaartekracht. Deze kracht zorgt ervoor dat de bal valt met een constante versnelling van 9.8 m/s².

Bijna niemand denkt echter na over het feit dat de bal ook een kracht van aantrekkingskracht op de aarde uitoefent. Natuurlijk blijft de aarde onveranderlijk, omdat de massa ervan veel groter is dan die van de bal en daarom een ​​verachtelijke versnelling ervaart.

Een ander opmerkelijk probleem over de derde wet van Newton is dat het contact tussen de twee objecten die op elkaar inwerken niet nodig is. Het is duidelijk met het voorbeeld dat zojuist is aangehaald: de bal maakt nog steeds geen contact met de aarde, maar toch oefent het toch zijn aantrekkingskracht uit. En de bal op de aarde ook.

Een kracht als zwaartekracht, die door elkaar werkt, zowel als er contact is tussen objecten alsof er geen naam is van "afstandsacties". In plaats daarvan krachten zoals wrijving en normaal, vereisen ze dat de objecten die op elkaar inwerken in contact zijn, dus worden ze "contactkrachten" genoemd.

Formules die uit het voorbeeld zijn geëxtraheerd

Terugkeren naar de paar balobjecten - de aarde, de P -tarieven voor de bal en T voor de aarde kiezen en de tweede wet van Newton op elke deelnemer in dit systeem worden toegepast, wordt verkregen:

Het kan u van dienst zijn: discrete variabele: kenmerken en voorbeelden

F_resulterend = m.naar

De derde wet stelt dat:

M_Pnaar_P = - m_Tnaar_T

naar_P = 9.8 m/s² verticaal gericht. Omdat deze beweging plaatsvindt langs de verticale richting kan worden verdeeld met de vectornotatie (BOLD); En de richting als positief en naar beneden kiezen als negatief, heb je:

naar_P = 9,8 m/s²

M_T ≈ 6 x 10 ²⁴ Kg

Ongeacht de massa van de bal, de versnelling van de aarde is nul. Daarom wordt opgemerkt dat de bal naar de aarde valt en niet andersom.

Werking van een raket

De Rockets vormen een goed voorbeeld van de toepassing van de derde wet van Newton. De raket die in de afbeelding in het begin wordt getoond, stijgt dankzij de voortstuwing van heet gas met hoge snelheid.

Velen geloven dat dit gebeurt omdat deze gassen op de een of andere manier de atmosfeer of op de grond "ondersteunen" om de raket te ondersteunen en te duwen. Het werkt niet zo.

Terwijl de raket sterkte op de gassen uitoefent en ze terugbrengt, oefenen de gassen een kracht uit op de raket, die dezelfde module heeft, maar tegenovergestelde richting. Deze kracht is degene die de raket met zijn versnelling biedt.

Als u geen raket hiervan met de hand hebt, zijn er andere manieren om te verifiëren dat de derde wet van Newton werkt om voortstuwing te bieden. Waterraketten kunnen worden gebouwd, waarbij de noodzakelijke stuwkracht wordt aangeboden door het water per drukgas.

Opgemerkt moet worden dat het begin van een waterraket tijd kost en veel voorzorgsmaatregelen nodig hebben.

Gebruik van schaatsen

Een meer betaalbare en onmiddellijke manier om het effect van de derde wet van Newton te verifiëren, is het plaatsen van een paar schaatsen en het promoten van een muur.

Meestal is het vermogen om kracht uit te oefenen met objecten die in beweging zijn geassocieerd, maar de waarheid is dat immobiele objecten ook kracht kunnen uitoefenen. De skater wordt teruggedreven dankzij de kracht die de onbeweeglijke erop uitgeeft.

Contactoppervlakken oefenen contactkrachten uit (normaal) met elkaar. Wanneer een boek wordt ondersteund op een horizontale tabel, oefent het een normale verticale kracht uit. Het boek oefent op de tabel een verticale kracht uit van dezelfde numerieke waarde en tegengestelde zin.

Kinderexperiment: skaters

Kinderen en volwassenen kunnen de derde wet van Newton ervaren en verifiëren dat actie- en reactietroepen niet worden geannuleerd en in staat zijn om bewegingen te bieden.

Twee skaters op het ijs of op een zeer glad oppervlak kunnen elk worden voortgestuwd.

Overweeg twee skaters met een heel ander deeg. Ze bevinden zich midden in een ijsbaan met verachtelijke wrijving en zijn in eerste instantie in rust. Op een bepaald moment duwen ze elkaar aan en duwen ze constante sterkte toe met de handpalmen van de handen. Hoe zullen beide bewegen?

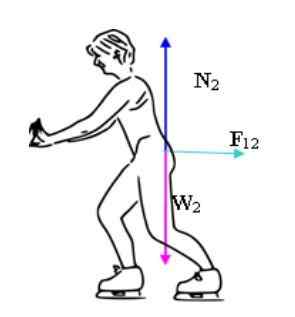
Kan u van dienst zijn: Balancing Vector: berekening, voorbeelden, oefeningenTwee skaters worden gedreven in het midden van een ijsbaan. Bron: Benjamin Crowell (Wikipedia User Bcrowell) [CC BY-SA 3.0 (http: // creativeCommons.Org/licenties/by-sa/3.0/]]

Het is belangrijk om te benadrukken dat, omdat het een oppervlak is zonder wrijving, de enige onevenwichtige krachten de krachten zijn die skaters elkaar aanbrengen. Hoewel het gewicht en de normale handel op beiden werken, zijn deze krachten in evenwicht, van wat de skaters in een verticale richting zouden versnellen.

Formules toegepast in dit voorbeeld

De derde wet van Newton stelt dat:

F₁₂ = -F_eenentwintig

Dat wil zeggen, de kracht die wordt uitgeoefend door skater 1 op de 2, is hetzelfde in grootte waar de 2 op de 1 uitoefenen, met dezelfde richting en de tegenovergestelde richting. Merk op dat deze krachten op verschillende objecten worden toegepast, op dezelfde manier dat de krachten op de bal en de aarde waren in het vorige conceptuele voorbeeld.

M₁ naar₁ = -m₂ naar₂

Omdat de krachten tegenover zijn, zullen de versnellingen die ook veroorzaken ook zijn, maar hun magnitudes zullen anders zijn, omdat elke skater een andere massa heeft. Laten we eens kijken naar de versnelling die door de eerste skater is verkregen:

Als de massa van de eerste skater groter is dan die van de tweede, zal de versnelling lager zijn. Dit is te verwachten omdat het een grotere traagheid heeft. De lichtste skater verwerft een grotere versnelling. Als de massa hetzelfde is, zullen de versnellingen ook zijn.

Dus de beweging die hieronder gebeurt, is de scheiding van beide skaters in tegengestelde zintuigen. In principe waren de skaters in het midden van de baan in rust. Elk oefent een kracht uit op de andere die een versnelling biedt terwijl de handen in contact zijn en de stuwkracht duurt.

Daarna gaan de skaters van elkaar weg met uniforme rechtlijnige beweging, door niet onevenwichtige krachten te handelen. De snelheid van elke skater zal anders zijn als hun massa ook zijn.

Oefening opgelost

Om problemen op te lossen waarin de wetten van Newton moeten worden toegepast, is het noodzakelijk om de krachten die op het object handelen zorgvuldig te tekenen. Deze tekening wordt "Free Body Diagram" of "geïsoleerd lichaamsdiagram" genoemd. In dit diagram mogen de krachten die het lichaam op andere objecten uitoefent niet worden getoond.

Als er meer dan één object bij het probleem betrokken is, is dit noodzakelijk.

1- De skaters van de vorige sectie hebben respectieve massa m₁ = 50 kg en m₂ = 80 kg. Ze duwen elkaar met een constante kracht van 200 n. De stuwkracht heeft een duur van 0.40 seconden. Vinden:

a) De versnelling die elke skater is verkregen dankzij de stuwkracht.

b) de snelheid van elk wanneer ze scheiden

Oplossing

a) Neem als een horizontaal positief adres dat van links naar rechts gaat. Het toepassen van de tweede wet van Newton met de waarden die door de verklaring worden verstrekt, is:

F_eenentwintig = m₁naar₁

Waar vandaan:

Voor de tweede skater:

b) Om de snelheid te berekenen die ze dragen net wanneer ze gescheiden zijn, worden de kinematische vergelijkingen van de uniform versnelde rechtlijnige beweging gebruikt:

Kan u van dienst zijn: wederzijdse inductantie: formule/coëfficiënt, toepassingen, oefeningen

De initiële snelheid is 0, omdat ze in het midden van de baan in rust waren:

v_F = AT

v_F1 = a₁t = -4 m/s² . 0.40 s = -1.6 m/s

v_F2 = A₂T = +2.5 m/s² . 0.40 s = +1 m/s

Resultaat

Zoals verwacht, verwerft persoon 1 lichter een grotere versnelling en dus snellere snelheid. Let nu op het volgende over het product van het deeg vanwege de snelheid van elke skater:

M₁ v₁ = 50 kg . (-1.6 m/s) = - 80 kg.Mevr

M₂ v₂ = 80 kg . 1 m/s = +80 kg.Mevr

De som van beide producten is 0. Het product van de massa door snelheid wordt de hoeveelheid beweging P genoemd. Het is een vector met dezelfde richting en snelheidsgevoel. Toen de skaters in rust waren en hun handen in contact waren, kan worden aangenomen dat ze hetzelfde object vormden waarvan de hoeveelheid beweging was:

P_of = (m₁ +M₂) v_of = 0

Nadat de stuwkracht is voltooid, blijft de hoeveelheid beweging van het schaatssysteem 0. Daarom wordt de hoeveelheid beweging behouden.

Voorbeelden van de derde wet van Newton in het dagelijks leven

Wandeling

Wandelen is een van de meest dagelijkse acties die kunnen worden uitgevoerd. Indien zorgvuldig waargenomen, moet de lopende actie de voet tegen de grond duwen, zodat deze een gelijke en tegengestelde kracht op de voet van de wandelaar terugkeert.

Toen we constant de derde wet van Newton toepassen. Bron: Pixabay.

Het is precies die kracht waarmee mensen kunnen lopen. Tijdens de vlucht oefenen de vogels de kracht op de lucht uit en duwt de lucht de vleugels zodat de vogel naar voren wordt gereden.

Beweging van een auto

In een auto oefenen de wielen kracht uit op de stoep. Dankzij de bestratingsreactie oefent het op de bandenstroepen die de auto naar voren drijven.

Sport

In de sportpraktijk zijn de actie- en reactiekrachten talrijk en hebben ze een zeer actieve deelname.

Laten we bijvoorbeeld de atleet bekijken met de voet ondersteund door een startblok. Het blok biedt een normale kracht als reactie op de stuwkracht die de atleet erop uitoefent. Het resultaat van dit normale en het gewicht van de gang, resulteert in een horizontale kracht waarmee de atleet naar voren kan rijden.

De atleet gebruikt het startblok om impuls naar voren toe te voegen bij de uitvoer. Bron: Pixabay.

Vuurslangen

Een ander voorbeeld waarin de derde wet van Newton aanwezig is, is in brandweerlieden die brandslangen houden. Het einde van deze grote slangen heeft een handvat op het mondstuk dat de brandweerman moet vasthouden wanneer de waterstraal uitkomt, om de tegenslag te voorkomen die optreedt wanneer het water op volle snelheid uitkomt.

Om dezelfde reden is het handig.

Referenties

1. Giancoli, D.  2006. Fysica: principes met toepassingen. Zesde editie. Prentice Hall. 80 - 82.
2. Rex, a. 2011. Fundamentals of Physics. Pearson. 73 - 75.
3. Tipler, p. 2010. Fysiek. Deel 1. 5e editie. Redactioneel teruggekeerd. 94 - 95.
4. Stern, D. 2002. Astronomen naar astronaves. Genomen van: PWG.GSFC.pot.Gov.