Bolzano stelling

We leggen uit wat de stelling van Bolzano is, de toepassingen en het opgeloste oefeningen

Wat is de stelling van Bolzano?

Hij Bolzano stelling Het stelt vast dat als een functie op alle punten van een gesloten interval [a, b] continu is en dat het beeld van "a" en "b" (onder de functie) tegengestelde tekenen heeft, dan zal er tenminste zijn Eén punt "C" in het open interval (A, B), zodat de geëvalueerde functie in "C" gelijk zal zijn aan 0.

Deze stelling werd vermeld door de filosoof, theoloog en wiskundige Bernard Bolzano in 1850. Deze wetenschapper, geboren in de huidige Tsjechische Republiek, was een van de eerste wiskunde in de geschiedenis die een formele demonstratie maakte van de eigenschappen van continue functies.

Verklaring van de stelling

De stelling van Bolzano staat ook bekend als de stelling van tussenliggende waarden, die helpt bij het bepalen van specifieke waarden, met name nullen, van bepaalde echte functies van een echte variabele.

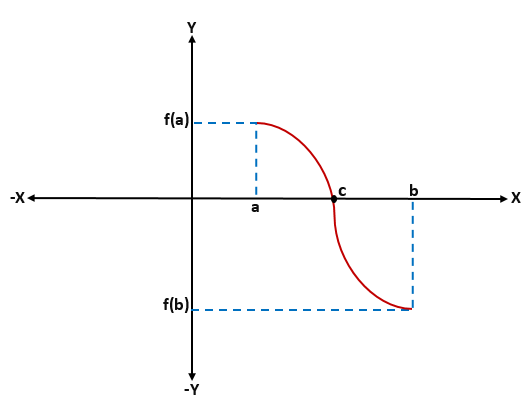
In een gegeven functie f (x) gaat verder -dat wil zeggen dat f (a) en f (b) zijn verbonden door een curve-, waarbij f (a) onder de x -as is (is negatief) en f (b) Door boven de x -as (het is positief), of vice versa, zal er een snijpunt op de x -as zijn dat een tussenliggende waarde "C" zal vertegenwoordigen, die tussen "A" en "B" zal zijn, en de waarde van f (c) het zal gelijk zijn aan 0.

Bij het grafisch analyseren van de stelling van Bolzano kan bekend zijn dat voor elke continue F -functie gedefinieerd in een interval [A, B], waarbij F (A)_*F (b) is minder dan 0, er zal ten minste één wortel "c" van die functie zijn binnen het interval (a, b).

Deze stelling bepaalt niet het aantal punten dat in dat open interval bestaat, het stelt slechts dat er minstens 1 punt is.

Demonstratie van de stelling van Bolzano

Om de stelling van Bolzano aan te tonen, wordt aangenomen zonder verlies van algemeenheid die f (a) 0; Op deze manier kunnen er veel waarden zijn tussen "a" en "b" waarvoor f (x) = 0, maar het is alleen nodig om aan te tonen dat er een is.

Kan u van dienst zijn: denkbeeldige getallen: eigenschappen, toepassingen, voorbeelden

Het begint F te evalueren in het middelpunt (A+B)/2. Als f ((a+b)/2) = 0, eindigt de test hier; Anders is F ((A+B)/2) positief of negatief.

Een van de helften van het interval [a, b] wordt gekozen, zodat de tekenen van de aan de uiteinden geëvalueerde functie verschillend zijn. Dit nieuwe interval zal [A1, B1] zijn.

Als F nu wordt geëvalueerd in het middelpunt van [A1, B1] is niet nul, dan wordt dezelfde bewerking eerder uitgevoerd; Dat wil zeggen, de helft van dit interval dat voldoet aan de toestand van de borden wordt gekozen. Wees dit nieuwe interval [A2, B2].

Als dit proces doorgaat, zijn er twee opvolgingen an en bn, zodat:

an groeit en bn neemt af:

a ≤ a1 ≤ a2 ≤ ... ≤ een ≤ .. . ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Als de lengte van elk interval [AI, BI] wordt berekend, moet u:

B1-a1 = (b-a)/2.

B2-a2 = (b-a)/2².

.. .

bn-an = (b-a)/2^n.

Daarom is de limiet wanneer N de neiging heeft om oneindig van (bn-an) gelijk te zijn aan 0.

Het gebruik van dat an groeit en beperkt en bn neemt af en beperkt, er is een waarde "c" zodat:

a ≤ a1 ≤ a2 ≤ ... ≤ een ≤ .. .≤ c ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

De lim limiet is "C" en de limiet van bn is ook "C". Daarom is er, gezien elke A> 0, altijd een "n" zodat het interval [an, bn] in het interval is opgenomen (c-δ, c+δ).

Nu moet worden aangetoond dat f (c) = 0.

Als f (c)> 0, dan als f continu is, is er een ε> 0 zodanig dat f positief is gedurende het interval (c -ε, c+ε). Zoals hierboven vermeld, is er echter een "n" -waarde zodat f verandert in [an, bn] en bovendien is [an, bn] in (c -ε, c+ε), wat wat is wat is wat is een tegenstrijdigheid.

Als f (c) 0 zodanig dat f negatief is gedurende het interval (c -ε, c+ε); Maar er is een "n" -waarde die F in teken verandert [an, bn]. Het blijkt dat [an, bn] is opgenomen in (c -ε, c+ε), wat ook een tegenspraak is.

Kan u van dienst zijn: tekenen van groepering

Daarom, f (c) = 0 en dit is wat wilde worden aangetoond.

Waar is de Bolzano -stelling voor?

Uit de grafische interpretatie wordt de stelling van Bolzano gebruikt om wortels of nullen te vinden in een continue functie, via bisension (aanpak), wat een incrementele zoekmethode is die de intervallen altijd in 2 verdeelt in 2.

Dus als de functie ondertekenen over een interval verandert, wordt de F -functie geëvalueerd in het middelpunt, dat als volgt wordt uitgedrukt: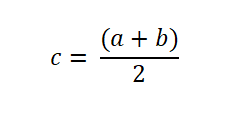De wortel wordt gevonden wanneer f (c) = 0. Zo niet, dan wordt het teken van F (c) geanalyseerd om te bepalen of het tegen het teken van F (a) of dat van F (b) is.

Vervolgens wordt een interval [a, c] of [c, b] genomen waar de verandering van teken optreedt en het proces wordt herhaald totdat het interval steeds minder is, om de gewenste waarde te benaderen; dat wil zeggen, tot de waarde dat de functie 0 doet.

Samenvattend, om de Bolzano -stelling toe te passen en zo de wortels te vinden, de nullen van een functie te beperken of een oplossing voor een vergelijking te geven, worden de volgende stappen uitgevoerd:

1. Het is geverifieerd als F een continue functie is in het interval [a, b].
2. Als het interval niet wordt gegeven, moet men er een vinden waar de functie continu is.
3. Het is geverifieerd als de uiteinden van het interval tegengestelde tekens geven wanneer het wordt geëvalueerd in F.
4. Als er geen tegengestelde tekenen worden verkregen, moet het interval worden onderverdeeld in twee subintervallen met behulp van het middelpunt.
5. Evalueer de functie in het middelpunt en verifieer dat aan de Bolzano -hypothese wordt voldaan, waar f (a) _* F (B) < 0.
6. Afhankelijk van het teken (positief of negatief) van de gevonden waarde, wordt het proces herhaald met een nieuwe subinterval totdat aan de genoemde hypothese is voldaan.

Kan u van dienst zijn: niet -lineaire programmering: methoden en oefeningen

Opgeloste oefeningen

Oefening 1

Bepaal of de functie f (x) = x² - 2, heeft ten minste één echte oplossing in het interval [1,2].

Oplossing

U hebt de functie f (x) = x² - 2. Zoals polynoom is, betekent dit dat het in elk interval continu is.

Er wordt gevraagd om te bepalen of het een echte oplossing heeft in het interval [1, 2], dus nu hoeft u alleen de uiteinden van het interval in de functie te vervangen om het teken hiervan te kennen en te weten of ze voldoen aan de voorwaarde van het zijn verschillend:

f (x) = x² - 2

f (1) = 1² - 2 = -1 (negatief)

f (2) = 2² - 2 = 2 (positief)

Daarom, teken van F (1) ≠ Sign F (2).

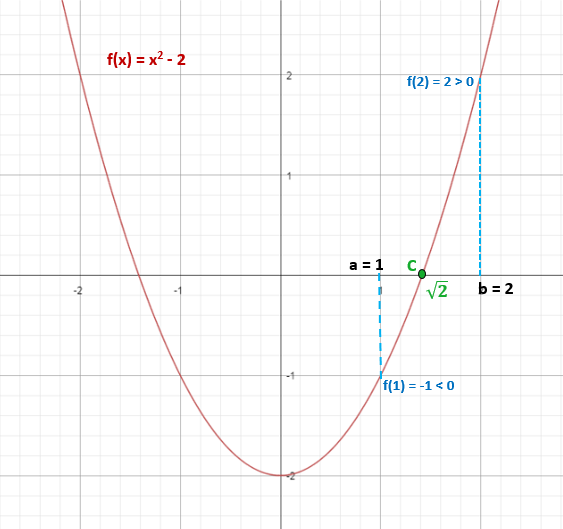
Dit zorgt ervoor dat er ten minste één punt "C" is dat behoort tot het interval [1,2], waarin f (c) = 0.

In dit geval kan de "C" -waarde gemakkelijk als volgt worden berekend:

X² - 2 = 0

x = ± √2.

Aldus behoort √2 ≈ 1.4 tot het interval [1,2] en vervult dat f (√2) = 0.

Oefening 2

Toon aan die vergelijking x⁵ + x + 1 = 0 heeft ten minste één echte oplossing.

Oplossing

Eerst merken we op dat f (x) = x⁵ + X + 1 is een polynoomfunctie, wat betekent dat deze in alle reële getallen continu is.

In dit geval wordt geen interval gegeven, dus u moet intuïtief waarden kiezen, bij voorkeur dicht bij 0, om de functie te evalueren en de wijzigingen van het teken te vinden:

Als het interval [0, 1] wordt gebruikt, moet het:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Omdat er geen tekenwijziging is, wordt het proces met een ander interval herhaald.

Als het interval [-1, 0] wordt gebruikt, moet u:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

In dit interval is er een tekenwijziging: teken van f (-1) ≠ teken van f (0), wat betekent dat de functie f (x) = x⁵ + X + 1 heeft ten minste één echte root "c" in het interval [-1, 0], zodat f (c) = 0. Met andere woorden, het is waar dat x⁵ + X + 1 = 0 heeft een echte oplossing in het interval [-1,0].