Som van polynomen, zoals wordt gedaan, voorbeelden, oefeningen

De Som van polynomen Het is de operatie die bestaat uit het toevoegen van twee of meer polynomen, wat resulteert in een ander polynoom. Om het uit te voeren is het noodzakelijk om de voorwaarden van dezelfde volgorde van elk van de polynomen toe te voegen en de resulterende som aan te geven.

Eerst bekijken we kort de betekenis van "voorwaarden van dezelfde volgorde". Een polynoom van iemand bestaat uit bedragen en/of aftrekking van termen.

Figuur 1. Om twee polynomen toe te voegen, is het noodzakelijk om ze te bestellen en vervolgens de vergelijkbare voorwaarden te verminderen. Bron: Pixabay + Wikimedia Commons.

De termen kunnen producten van reële getallen en een of meer variabelen zijn, bijvoorbeeld weergegeven met letters, bijvoorbeeld: 3x² en -√5.naar²BC³ Het zijn voorwaarden.

Welnu, de voorwaarden van dezelfde volgorde zijn die met dezelfde exponent of kracht, hoewel ze misschien een andere coëfficiënt hebben.

-Voorwaarden van gelijke volgorde zijn: 5x³, √2 x³ en -1/2x³

-Verschillende bestellingenvoorwaarden: -2x^-2, 2xy^-1 en √6x²En

Het is belangrijk om in gedachten te houden dat alleen de voorwaarden van dezelfde volgorde kunnen worden toegevoegd of afgetrokken, een bewerking die bekend staat als afname. Anders wordt de som gewoon aangegeven aangegeven.

Zodra het concept van termen van dezelfde volgorde is verduidelijkt, worden de polynomen toegevoegd volgens deze stappen:

-Volgorde Eerst de polynomen om toe te voegen, allemaal op dezelfde manier, ofwel toenemende of afnemende, dat wil zeggen, met de bevoegdheden van minst naar de grootste of vice versa.

-Vervolledigen, In het geval dat elke kracht in de reeks ontbreekt.

-Verminderen De vergelijkbare termen.

-Aanwijzen De resulterende som.

[TOC]

Polynomiale som voorbeelden

We zullen beginnen met het toevoegen van twee polynomen met een enkele variabele genaamd X, Bijvoorbeeld de polynomen p (x) en q (x) gegeven door:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Na de beschreven stappen begint het door ze af te nemen, wat de meest gebruikelijke manier is:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Het kan u van dienst zijn: ingeschreven hoek van een cirkel: definitie, stellingen, voorbeelden

Q (x) = x⁵+ X² - 25x

Polynomiale Q (x) is niet compleet, het is te zien dat krachten met exponent 4, 3 en 0. De laatste is gewoon de onafhankelijke term, degene die geen brief heeft.

Q (x) = x⁵+ 0x⁴ + 0x³ + X² - 25x + 0

Zodra deze stap is voltooid, zijn ze klaar om toe te voegen. U kunt de vergelijkbare termen toevoegen en vervolgens de som aangeven, of de polynomen die door elkaar worden besteld en op deze manier door kolommen worden besteld: op deze manier:

- X⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ X⁵ + 0x⁴ + 0x³  +  X²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

Het is belangrijk op te merken dat wanneer toegevoegd, het algebraïsch wordt gedaan met betrekking tot de tekenregel, op deze manier 2x + (-25 x) = -23x. Dat wil zeggen, als de coëfficiënten een ander teken hebben, worden afgetrokken en het resultaat het teken van de major draagt.

Voeg twee of meer polynomen toe met meer dan één variabele

Als het gaat om polynomen met meer dan één variabele, wordt een daarvan gekozen om het te bestellen. Stel bijvoorbeeld dat het wordt gevraagd toe te voegen:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

EN:

T (x, y) = ½ x²- 6y²  - 11xy + x³En

Een van de variabelen wordt gekozen, bijvoorbeeld de X om te bestellen:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

De ontbrekende voorwaarden worden onmiddellijk voltooid, volgens welke elke polynoom heeft:

R (x, y) = 0x³en + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6y² 

En beide zijn klaar om vergelijkbare termen te verminderen:

0x³en + 5x² +  8xy - 6y³  - 4y²

Kan u van dienst zijn: Bepalingscoëfficiënt: formules, berekening, interpretatie, voorbeelden

+ X³y + ½ x² - 11xy + 0y³ - 6y²       +

-

+ X³Y + 11/2x² - 3xy - 6y³  - 10y²    = R (x, y) + t (x, y)

Polynomiale somoefeningen

- Oefening 1

Geef in de volgende som van polynomen de term aan die in de blanco moet gaan om de polynoomsom te verkrijgen:

-5x⁴  + 0x³ +  2x²         + 1

X⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Oplossing

Om -6x te verkrijgen⁵ Een term van de bijl is vereist⁵, zoals dat:

A + 1+ 2 = -6

Daarom:

A = -6-1-2 = -9

En de gezochte term is:

-9x⁵

-Ga op dezelfde manier door om de rest van de voorwaarden te vinden. Hier is exponent 4:

-5 + 2 + a = 10 → a = 10 + 5-2 = 13

De ontbrekende term is: 13x⁴.

-Voor X Powers³ Het is onmiddellijk dat de term -9x moet zijn³, Op deze manier is de kubieke term coëfficiënt 0.

-Wat betreft de vierkante krachten: A + 8 -14 = -11 → A = -11 -8 + 14 = -5 en de term is -5x².

-De lineaire term wordt verkregen door A +8 -14 = -11 → A = -11 + 14 -8 = -5, zijnde de ontbrekende term -5x.

-Ten slotte is de onafhankelijke term: 1 -3 + a = -21 → a = -19.

- Oefening 2

Een vlak terrein is omgeven zoals getoond in de figuur. Zoek een uitdrukking voor:

a) de omtrek en

b) het gebied, in termen van de aangegeven lengtes:

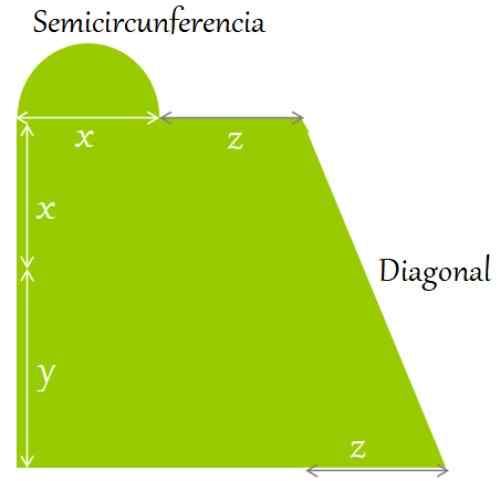Figuur 2. Een vlak terrein is omgeven door de vorm en aangegeven afmetingen. Bron: f. Zapata.

Oplossing voor

De perimeter wordt gedefinieerd als de som van de zijkanten en contouren van de figuur. Beginnend in de linkeronderhoek, in de richting van de klokken, heb je:

Het kan u van dienst zijn: Issmeles trapezoid: eigenschappen, relaties en formules, voorbeelden

Perimeter = y + x + halve cirkel lengte + Z + diagonale lengte + Z + z + x

De halve cirkel heeft een diameter gelijk aan x. Omdat de straal de helft van de diameter is, moet deze:

Radio = x/2.

De formule voor de lengte van een volledige omtrek is:

L = 2π x radio

Dus:

Halve cirkel lengte = ½. 2π (x/2) = πx/2

Van zijn kant wordt de diagonaal berekend met de stelling van Pythagoras die op de zijkanten wordt toegepast: (x+y) die verticale zijde en z is, wat de horizontale is:

Diagonal = [(x+y)² + Z²]^1/2

Deze uitdrukkingen worden vervangen in de omtrek, om te verkrijgen:

Perimeter = y + x + πx/2 + z + [(x + y)² + Z²]^1/2+ z + x + z

Soortgelijke termen worden verminderd, omdat de som vereist dat het resultaat tot het maximum wordt vereenvoudigd:

Perimeter = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + Z²]^1/2 = y + (2 + π /2) x + 3z

Oplossing B

Het resulterende gebied is de som van het rechthoekige gebied, de halve cirkel en de rechter driehoek. De formules voor deze gebieden zijn:

-Rechthoek: Basis X Hoogte

-Halve cirkel: ½ π (radio)²

-Driehoek: Basis x Hoogte /2

Rechthoekgebied

(x+y). (x+z) = x² + XZ + YX + YZ

Halve cirkelvormige gebied

½ π (x/2)² = π x² / 8

Gebied van de driehoek

½ z (x + y) = ½ zx + ½ ZY

Volledige oppervlakte

Om het totale gebied te vinden, worden de uitdrukkingen voor elk gedeeltelijk gebied toegevoegd:

Totale oppervlakte = x² + Xz + yx + yz + (π x² / 8) + ½ ZX + ½ ZY

En ten slotte alle termen die vergelijkbaar zijn:

Totale oppervlakte = (1 + π/8) x² + 3/2 XY + 3/2YZ + YX

Referenties

1. Baldor, een. 1991. Algebra. Venezolaanse culturele redactionele s.NAAR.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Wiskunde is leuk. Polynomen toevoegen en aftrekken. Hersteld van: MathsisFun.com.
4. Monterey Institute. Polynomen toevoegen en aftrekken. Hersteld van: Montereyinstitute.borg.
5. UC Berkeley. Algebra van polynomen. Hersteld van: wiskunde.Berkeley.Edu.