Samengestelde opvolging

Opvolging samengesteld uit gele en blauwe vierkanten. Bron: f. Zapata

Wat is een samengestelde opvolging?

A samengestelde opvolging Het bestaat uit een reeks elementen, gemaakt uit twee (of meer) verschillende en alternatieve opvolgingen. Elk van deze opvolgingen heeft een bepaalde regel, die wordt gebruikt om hun respectieve elementen te vinden.

De elementen hoeven niet numeriek te zijn, in staat zijn om figuren, symbolen of letters te zijn, maar die zijn gebaseerd op getallen worden aangeroepen rekenkundige opvolgingen. De figuur waarmee ons artikel begint, toont een samengestelde opvolging van gele en blauwe vierkanten.

In deze opeenvolging begint het vanuit een groot vierkant bestaande uit 8 gele vierkanten en een blauw vierkant. Om de volgende term te krijgen, wordt een geel vierkant toegevoegd aan de linkerkant of rechts van de eerste en derde rij vierkanten. De ruimte die resulteert in de centrale rij is gevuld met een blauw vierkant.

Elke figuur in de reeks wordt genoemd termijn. Als u de vijfde termijn wilt vinden, moet u een geel vierkant aan de rechterkant van de eerste en derde rangen toevoegen, en een blauw vierkant op de tweede rij:

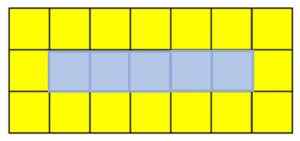Vijfde term van een opeenvolging van gele en blauwe vierkanten. Bron: f. Zapata

Uitleg

In samengestelde opvolgingen worden de termen verkregen door de voorwaarden van twee of meer onafhankelijke eenvoudige opvolgingen af ​​te wisselen. Om het idee beter te begrijpen, moet het de details van een eenvoudige opvolging worden beoordeeld.

De volgende eenvoudige opvolging bestaat bijvoorbeeld uit de natuurlijke getallen:

2, 4, 6, 8, 10, 12 ..

De suspensieve punten geven aan dat de opvolging oneindige termen heeft.

Elk van de voorwaarden wordt aangegeven door een kleine letter en een nummer, als een subscript. Dit nummer geeft de positie aan of inhoudsopgave van elke term. In de vorige opvolging kun je schrijven:

naar₁ = 2; naar₂ = 4; naar₃ = 6; naar₄ = 8 ..

Het is erg handig om een ​​manier te hebben om elke term die gewenst is van de opvolging te berekenen, dat wil zeggen de specifieke regel. Met haar de N-ÉSIMO-term, of Algemene term, aangeduid als een_N.

Kan u van dienst zijn: eigenschappen van gelijkheid

Doorgaan met het voorbeeld van de opeenvolging van gelijkmatige getallen, kunt u de manier vaststellen om de term n-Ésimo te berekenen, van de vorige termijn:

naar_N = A_N-1 + 2

Waarheen_N-1 Het is de term die voorafgaat_N.

Natuurlijk zou het beter zijn om de algemene term te kennen zonder afhankelijk te zijn van andere voorwaarden. In deze opeenvolging is het gemakkelijk op te merken dat elke term zich vermenigvuldigt met 2 de positie die het inneemt, gezien het subscript van de termijn. Op deze manier wordt het geschreven:

naar_N = 2n

De oude Grieken kenden al de opvolgingen van gelijkmatige en vreemde cijfers. De opeenvolging van vreemde natuurlijke getallen kan ondertussen worden geschreven als:

1, 3, 5, 7, 9, 11 ..

En het combineren van de opeenvolging van de gelijkmatige getallen met die van de oneven, is de volgende samengestelde opvolging:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Wiens resultaat de set van natuurlijke getallen is.

Voorwaarden van een samengestelde opvolging

Het kan leuk zijn om te proberen de relatie te vinden die bestaat in een reeks getallen, waarvoor het zorgvuldig moet worden waargenomen en proberen te bepalen of het een samengestelde opvolging is.

De algemene vorm van een opvolging die bestaat uit twee opvolgingen zal zijn:

naar₁, B₁, naar₂, B₂, naar₃, B₃, naar₄, B₄,..

Waarheen₁, naar₂, naar₃, naar₄,... zijn de voorwaarden van de eerste opvolging en B₁, B₂, B₃, B₄,... die van de tweede. Ze worden altijd afgewisseld, zoals in dit voorbeeld het geval is:

7, 8, 14, 16, eenentwintig, 24, 28, 32, 35..

Wat zal de term zijn die volgt?

Om te weten, ken de opvolging in twee alternatieve sets van getallen als volgt:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

In de eerste van deze sets verschijnen de veelvouden van 7:

naar₁ = 7 × 1 = 7; naar₂ = 7 × 2 = 14; naar₃ = 7 × 3 = 21; naar₄ = 7 × 4 = 28; naar₅ = 7 × 5 = 35

De algemene term van deze opvolging is:

naar_N = 7n

En in de tweede zijn het de veelvouden van 8:

B₁ = 8 × 1 = 8; B₂ = 8 × 2 = 16; B₃ = 8 × 3 = 24; B₄ = 8 × 4 = 32

Dus de algemene term is:

Het kan u van dienst zijn: echte echte variabele functie en de grafische weergave ervan

B_N = 8n

Terugkerend naar de oorspronkelijke samengestelde opvolging, behoort de 35 tot de eerste reeks, waarvan de voorwaarden zijn₁, naar₂, naar₃, naar₄ ... 35 is de vijfde termijn, dus de volgende term moet B zijn₅, die gemakkelijk uit de regel wordt verkregen om de algemene term te vinden:

B₅ = 8 × 5 = 40

En het is geschreven:

7, 8, 14, 16, eenentwintig, 24, 28, 32, 35, 40 ..

Voorbeelden van samengestelde opvolgingen

voorbeeld 1

U kunt een samengestelde opvolging creëren met geometrische figuren, zoals het vierkant en de cirkel, die ze rangschikken zoals hieronder getoond:

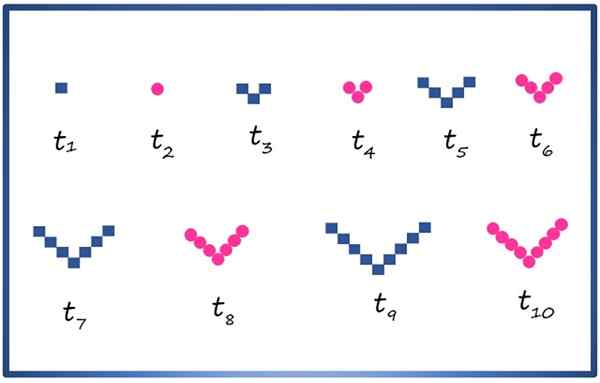De eerste 10 termen van een samengestelde opvolging met de vierkante geometrische elementen en cirkels. Bron: f. Zapata

Elke term wordt aangegeven door t₁, T₂, T₃, T₄ ..., de termen van Parque Index bestaan ​​uit cirkels en die van vreemde index, vierkanten. Zorgvuldig de volgorde waarnemen, is het mogelijk om bijvoorbeeld te weten dat de term t_elf, dat niet in de afbeelding verschijnt, bestaat uit 11 vierkanten met de bepaling in V.

Voorbeeld 2

De volgende samengestelde opvolging bestaat uit symbolen, in dit geval de letters R en S:

R SS RR SSS RRR SSS RRRR SSSS RRRR SSSSSSS ..

Elke nieuwe term wordt gebouwd door een brief toe te voegen aan de vorige. De eerste vier termen van de getoonde reeks zijn:

T₁= R ; T₂= H.H ; T₃= RR ; T₄= SSS ..

En de volgende term die zou verschijnen nadat de getoonde voorwaarden is: is:

T_elf= Rrrrr

Voorbeeld 3

De eerdere voorbeelden toonden oplopende opvolgingen, waarin elke waarde op een of andere manier toeneemt met betrekking tot de vorige. Maar het hoeft niet altijd op deze manier te zijn, omdat de opvolgingen kunnen dalen, dat wil zeggen dat ze een afname -patroon hebben.

En stijgende opvolgingen kunnen worden gecombineerd met dalende opvolgingen.

De volgende numerieke opvolging is samengesteld:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Het kan worden gescheiden in twee opvolgingen:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Wat zijn de waarden die in de lege ruimtes moeten worden geplaatst?

Zorgvuldig observeren van de eerste opvolging, wordt elke term verkregen door 3 toe te voegen aan de voorgaande termijn. Het is daarom een ​​oplopende opvolging:

Kan u van dienst zijn: hoekige verplaatsing

7 = 4 + 3

10 = 7 + 3

Daarom moet je in de eerste lege ruimte plaatsen:

10 + 3 = 13

Hierna is de volgende term in feite:

16 = 13 + 3

En degene die in de tweede blanco gaat, is:

16 + 3 = 19

De tweede opvolging daalt af en het is heel eenvoudig om de ontbrekende voorwaarden te vinden, omdat wordt opgemerkt dat elke term wordt verkregen door 1 af te trekken van de vorige termijn, daarom:

36, 35, 3. 4, 33, 32..

Eindelijk kun je schrijven:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Opgeloste oefeningen

Oefening 1

In de opeenvolging van voorbeeld 3 in de voorgaande sectie:

a) behoort 29 tot de opvolging?

b) Schrijf nog 10 voorwaarden van deze opvolging

Antwoord op

Ja, het hoort erbij, omdat de tweede opvolging daalt en de voorwaarden ervan worden verkregen door 1 af te trekken van de vorige termijn. Op deze manier bereikt het uiteindelijk 29.

Antwoord B

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Merk op dat sommige termen worden herhaald.

Oefening 2

Zoek de ontbrekende termen in de volgende samengestelde opvolging:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Antwoord

De vreemde termen zijn geschreven om de eerste opvolging te verkrijgen:

100, 115, 130, 145, 160, ..

Opgemerkt wordt dat u, om elke term te vinden, 15 aan de vorige termijn moet toevoegen, daarom is de term die volgt op 160 175.

De tweede opvolging bestaat uit:

500, 480, 460, 440, 420, ..

Elke term verschilt van de vorige bij 20, de opvolging die daalt, daarom is de term die wordt gevolgd op 420 400.

Met deze informatie worden nog twee termen toegevoegd aan de oorspronkelijke samengestelde opvolging, zoals deze:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Referenties

1. Larson, r. (2012). Voorzetting. 8e. Editie. Cengage leren.
2. Stewart, J. (2007). Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
3. Samengestelde opvolgingen. Hersteld van: media.Educacioncampeche.Gok.mx.
4. Numerieke opvolgingen. Opgehaald uit: MatemathWeb.com.
5. Opvolgingen. Rekenkundige en geometrische progressies. Opgehaald uit: Macmillaneducation.is.