Reeks krachtvoorbeelden en oefeningen

A Kracht series Het bestaat uit een som van termen in de vorm van bevoegdheden van de variabele X, of meer in het algemeen, van X-C, waar C Het is een constant reëel getal. In de samenvatting van de som een ​​reeks bevoegdheden wordt het als volgt uitgedrukt:

∑a_N (X -c)^N = a_of + naar₁ (x - c) + a₂ (X - c)² + naar₃ (X - c)³ +… + A_N (X - c)^N

Waar de coëfficiënten_of, naar₁, naar₂... het zijn reële getallen en de serie begint op n = 0.

Figuur 1. Definitie van een Power -serie. Bron: f. Zapata.

Deze serie is gericht op waarde C dat is constant, maar dat kun je kiezen C Gelijk zijn aan 0, in welk geval de bevoegdheden zijn vereenvoudigd:

∑a_N X^N = a_of + naar₁ x + a₂ X² + naar₃ X³ +… + A_N X^N

De serie begint met naar_of(X-C)⁰ En naar_ofX⁰ respectievelijk. Maar we weten dat:

(X-C)⁰= x⁰ = 1

Daarom naar_of(X-C)⁰ = naar_ofX⁰ = naar_of (Onafhankelijke termijn)

Het goede van de krachten van de krachten is dat u met hen functies kunt uiten en dit heeft veel voordelen, vooral als u met een gecompliceerde functie wilt werken.

Wanneer dit het geval is, in plaats van direct de functie te gebruiken, wordt de stroomontwikkeling gebruikt, die gemakkelijker kan worden afgeleid, integreren of numeriek kunnen werken.

Natuurlijk is alles geconditioneerd voor de convergentie van de serie. Een serie convergeert wanneer door een bepaalde hoeveelheid termen toe te voegen, een vaste waarde wordt verkregen. En als we meer termen toevoegen, blijven we die waarde verkrijgen.

[TOC]

Functioneert als krachten van krachten

Als een voorbeeld van een functie die wordt uitgedrukt als een reeks kracht, laten we nemen F (x) = e^X.

Deze functie kan als volgt worden uitgedrukt in termen van een reeks krachten:

En^X  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) +..

Waar! = n. (N-1). (N-2). (N-3) ... en het is genomen 0! = 1.

We gaan controleren met behulp van een rekenmachine, die de serie effectief samenvalt met de expliciet gegeven functie. Laten we bijvoorbeeld beginnen met x = 0.

Kan u van dienst zijn: theoretische waarschijnlijkheid: hoe u het uit kunt krijgen, voorbeelden, oefeningen

We weten dat e⁰ = 1. Laten we eens kijken wat de serie doet:

En⁰ ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +… = 1

En laten we het nu proberen x = 1. Een rekenmachine gooit dat En¹ = 2.71828, En laten we dan vergelijken met de serie:

En¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) +… = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +… ≈ 2.7167

Met slechts 5 termen hebben we al exact toeval in E ≈ 2.71. Onze serie mist net iets meer, maar naarmate er meer termen worden toegevoegd, convergeert de serie met alle zekerheid de exacte waarde van En. De weergave is precies wanneer N → ∞.

Als de vorige analyse wordt herhaald n = 2 Er worden zeer vergelijkbare resultaten verkregen.

Op deze manier zijn we er zeker van dat de exponentiële functie f (x) = e^X Het kan worden vertegenwoordigd door deze reeks krachten:

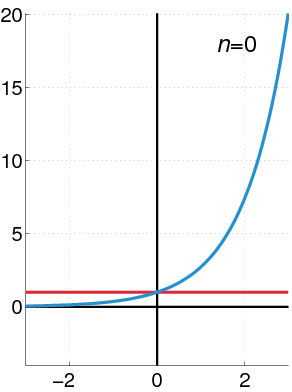Figuur 2. In deze animatie wordt het gezien als de krachten dichter bij de exponentiële functie zijn naarmate er meer termen worden genomen. Bron: Wikimedia Commons.

Geometrische krachten van krachten

De functie f (x) = e^X Het is niet de enige functie die een seriële weergave van bevoegdheden toelaat. Bijvoorbeeld de functie  F((x) = 1/1 - x  Het lijkt veel op het bekende Convergente geometrische serie:

∑a.R^N = A / 1 - r

Doe gewoon a = 1 en r = x om een ​​geschikte serie te verkrijgen voor deze functie, die is gecentreerd op c = 0:

Het is echter bekend dat deze serie convergent is voor │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Wanneer u deze functie in een ander interval wilt definiëren, richt deze zich gewoon op een adequate waarde en klaar.

Hoe u de serieontwikkeling van krachten van een functie kunt vinden

Elke functie kan worden ontwikkeld in een reeks bevoegdheden gericht op C, zolang je hebt afgeleid van alle bestellingen bij x = c. De procedure maakt gebruik van de volgende stelling, geroepen Taylor Stelling:

Laat f (x) een functie zijn met orderderivaten N, aangeduid als F^(N), die een seriële ontwikkeling van bevoegdheden in de interval toelaat Je. Zijn ontwikkeling in Taylor -serie is:

Het kan u van dienst zijn: wat is de locatie van hele en decimale nummers?

Zodat:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² /2 + f "(c) (x-c)³ /6 +... r_N

Waar r_N, dat is de nde van de serie, het wordt genoemd residu:

Wanneer c = 0 wordt de serie genoemd Maclaurin -serie.

Deze hier gegeven serie is identiek aan de in het begin gegeven serie, alleen nu is er een manier om de coëfficiënten van elke term expliciet te vinden, gegeven door:

Er moet er echter voor worden gezorgd dat de serie de functie overbrengt die u wilt vertegenwoordigen. Het gebeurt dat niet elke Taylor -serie noodzakelijkerwijs convergeert naar de F (x) die in gedachten was bij het berekenen van de coëfficiënten naar_N.

Dit gebeurt omdat misschien die zijn afgeleid van de functie, geëvalueerd in x = c Val samen met dezelfde waarde van die afgeleid van een ander, ook in x = c. In dit geval zouden de coëfficiënten hetzelfde zijn, maar de ontwikkeling zou dubbelzinnig zijn door niet de zekerheid te hebben met welke functie overeenkomt.

Gelukkig is er een manier om te weten:

Convergentie criteria

Om dubbelzinnigheid te voorkomen, als r_N → 0 Wanneer n → ∞ voor alle x in interval I, convergeert de serie naar f (x).

Oefening

- Oefening opgelost 1

Vind de geometrische krachten voor functie f (x) = 1/2 - x gericht op C = 0.

Oplossing

De gegeven functie moet worden uitgedrukt op een manier die zoveel mogelijk overeenkomt met 1 / 1- x, waarvan de serie bekend is. Daarom herschrijven we teller en noemer, zonder de oorspronkelijke uitdrukking te wijzigen:

1/2 - x = (1/2) / [1 - (x / 2)]

Omdat ½ constant is, gaat het uit de som, en dit wordt geschreven in termen van de nieuwe variabele x/2:

Kan u van dienst zijn: geconjugeerd binomiaal: hoe het is opgelost, voorbeelden, oefeningen

Merk op dat x = 2 niet tot het domein van de functie behoort en volgens de convergentiecriteria in de sectie Power geometrische serie, Ontwikkeling is geldig voor │x/2│< 1 o equivalentemente -2 < x < 2.

- Oefening opgelost 2

Zoek de eerste 5 termen van de serieontwikkeling van Maclaurin van de functie F (x) = sen x.

Oplossing

Stap 1

Ten eerste zijn de derivaten:

-Afgeleid van orde 0: het is dezelfde functie f (x) = sen x

-Eerste afgeleide: (sin x) '= cos x

-Tweede derivaat: (sin x) "= (cos x) '= - sin x

-Derde afgeleide: (sin x) "= (-sen x) '= - cos x

-Vierde afgeleide: (sin x) "= (- cos x) '= sin x

Stap 2

Vervolgens wordt elk derivaat geëvalueerd op x = c, evenals een ontwikkeling van maclaurine, c = 0:

sin 0 = 0; cos 0 = 1; - Sen 0 = 0; -Cos 0 = -1; Sin 0 = 0

Stap 3

De coëfficiënten zijn gebouwd_N;

naar_of = 0/0! = 0; naar₁ = 1/1! = 1; naar₂ = 0/2! = 0; naar₃ = -1 / 3!; naar₄ = 0/4! = 0

Stap 4

Eindelijk wordt de serie geassembleerd volgens:

sin x ≈ 0.X⁰ + 1. X¹ + 0 .X² - (1/3!) X³ + 0.X⁴... = x - (1/3!)) X³  +..

Heeft de lezer meer voorwaarden nodig?? Hoeveel meer, de serie is dichter bij de functie.

Merk op dat er een patroon is in de coëfficiënten, de volgende niet -nul term is₅ En alle vreemde index verschillen ook van 0, die de tekens afwisselen, zodat:

Sen x ≈ X - (1/3!)) X³  + (1/5!)) X⁵ - (1/7!)) X⁷  +.. .

Het wordt achtergelaten als oefening om te verifiëren, u kunt de verhouding van het quotiënt Voor serieconvergentie.

Referenties

1. CK-12 Foundation. Power Series: weergave van functies en bewerkingen. Hersteld van: CK12.borg.
2. Engler, a. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Integrale calculus. Nationale Universiteit van de kust.
3. Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
4. Gratis wiskundeteksten. Kracht series. Hersteld van: wiskunde.Liibretexts.borg.
5. Wikipedia. Kracht series. Hersteld van: is.Wikipedia.borg.