Eigenschappen van Fibonacci -serie, natuurlijke relaties, toepassingen

De O -serie Fibonacci -opvolging is een reeks getallen die wordt verkregen door te beginnen met 0 en 1, gaat door met de som ervan: 0 + 1 = 1, dan de som van de vorige twee: 1 + 1 = 2, enzovoort,.

Na deze procedure worden de andere termen verkregen, laten we zien: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13 ..

Eerste nummers van de Fibonacci -serie

De procedure wordt zo vaak herhaald als u wilt. Op deze manier verwerft de opvolging van Fibonacci de vorm: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. De cijfers die het maken worden genoemd Fibonacci -nummers.

[TOC]

Geschiedenis

De opvolging van Fibonacci wordt een Italiaanse wiskundige genoemd die in de middeleeuwen leefde: Leonardo de Pisa, ook bekend als Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo bracht jeugd door in Noord -Afrika en reisde door de Middellandse Zee, waar hij het Indo -Arabische nummeringssysteem kende en blij met hem was. Waarschijnlijk leerden de Arabische leraren van Leonardo hem over de opvolging, die al bekend was bij hindoe -wiskundigen.

Vervolgens schreef bij terugkeer naar Pisa Fibonacci een boek met de naam Liber Abaci ).

En de oplossing voor dit probleem is precies het aantal van de fibonacci -opvolging.

Leonardo de Pisa ontving niet de oprichting van de opvolging; Hij noemde het alleen in zijn boek als een nieuwsgierigheid, die de aandacht trok van veel geleerden die hem volgden. Onder deze was de negentiende -eeuwse Franse wiskundige Edouard Lucas, die bij het bestuderen van de opvolging haar doopte met de naam van de middeleeuwse wijze die het in het westen bekend maakte.

Het probleem van Fibonacci -konijnen

Het probleem zegt: er zijn een paar konijnen voor altijd, die na twee maanden vruchtbaar zijn. Zodra de volwassenheid is bereikt, hebben ze elke maand een paar baby's van verschillende seks, die ook twee maanden duren om zich voort te planten en een maandelijks een paar konijnen heeft.

Kan u van dienst zijn: de morgan wetten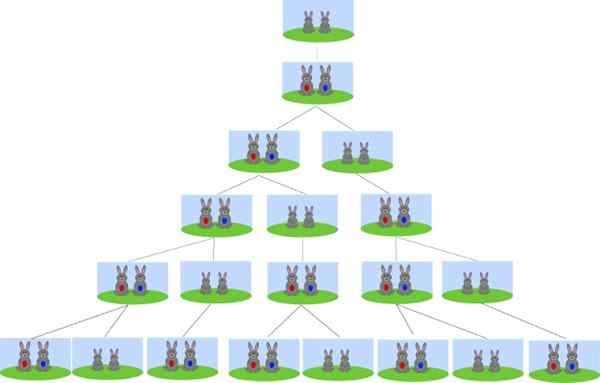De oorsprong van de opvolging van Fibonacci is in het probleem van de reproductie van konijnen. Bron: Wikimedia Commons.

Beginnend met een paar pasgeboren konijnen, hoeveel paar konijnen zijn er over een maand? Hoeveel paar konijnen zullen zijn na 2, 3 en 4 maanden? En hoeveel zullen er na 6 maanden zijn?

Het antwoord is in Fibonacci -getallen. Na 1 maand zijn er 1 paar konijnen, het oorspronkelijke paar, omdat ze zich pas na 2 maanden voortplanten.

Na 2 maanden zijn er 2 paren van konijnen: het originele paar en hun eerste nest.

Na 3 maanden hebben we 3 koppels, waaronder het oorspronkelijke paar, hun eerste nest en een nieuwe.

Bij het bereiken van de 4e maand hebben we het oorspronkelijke paar, het eerste nest dat op zijn beurt hun eerste kinderen heeft, het nest van de derde maand en een nieuw nest. In totaal 5 paar konijnen.

Maar dit zijn de aantallen van de Fibonacci -reeks, daarom zullen er na 6 maanden 13 paren van konijnen zijn, omdat elke maand de paren van de voorgaande twee maanden worden toegevoegd.

Fibonacci -serie eigenschappen

Hier zijn enkele interessante eigenschappen van de opvolging van de Fibonacci.

Eigendom 1

De recursieve formule om de voorwaarden van de opvolging te vinden is:

naar_N+1 = A_N + naar_N-1  Voor n groter dan of gelijk aan 2.

Waar n = 2, 3, 4, ... dat is, om de zevende term te vinden₇, We doen n = 6, zodat 6+1 = 7. We moeten de voorwaarden weten₅  al₆, van de lijst die verschijnt in de inleiding tot₅ = 5 en a₆ = 8, daarom₇ = 5+8 = 13.

Eigendom 2

Als de twee termen die we willen vinden niet bekend zijn, kunnen we de volgende formule gebruiken:

Het kan u van dienst zijn: Tesseldos: karakteristiek, typen (regelmatig, onregelmatig), voorbeelden

Eigendom 3

De cijfers a_N al_N+1 Zijn  Coprimos, dat wil zeggen, ze zijn neven met elkaar, wat betekent dat ze geen gemeenschappelijke factoren gemeen hebben.

Eigendom 4

Een zeer interessante eigenschap is dat van het quotiënt tussen de voorwaarden_2n al_N, die 1 waard is, wanneer n = 1. Het is te zeggen:

naar₂ / naar₁ = 1

We kunnen het eenvoudig controleren met de lijst met Fibonacci -nummers.

Aan de andere kant, als n ≠ 1, dan is het quotiënt:

naar_2n / naar_N = A_N  + 2e_N-1

Bijvoorbeeld als n = 3, dan a _2n = A₆ = 8 en₃ = 2. Nou dan:

8/2 = 2 + 2. naar₂ = 2 + 2. 1

Inderdaad: 8/2 = 4 en 2 + (2.1) = 4. Er kan worden geverifieerd dat aan elke N -waarde wordt voldaan.

Eigendom 5

De verhouding r_N = A_N+1 / naar_{N ,} Wanneer N groot wordt, kom je samen naar de Gouden reden of Aurea -aandeel, Een irrationeel getal dat zich vaak voorkomt in de natuur, gegeven door:

Natuurlijke relaties van de opvolging van de Fibonacci

Fibonacci's opvolging in planten

De manifestaties van de fibonacci -opvolging in overvloed in het plantenrijk

De takken van bepaalde bomen komen elk jaar uit volgens de opvolging van de Fibonacci. Het eerste jaar dat de kofferbak groeit zonder een tak te gooien, na een jaar produceert het er een en zo tijdens elk jaar. Op zijn beurt kan elke tak na een jaar nog een nieuwe gooien, net zoals de konijnen zich voortplanten.

Het centrum van de zonnebloembloemen bevat de zaden die zijn gerangschikt in logaritmische spiraalbundels, in beide zin, waarvan de hoeveelheden overeenkomen met twee opeenvolgende Fibonacci -getallen.

Fibonacci -nummers zijn aanwezig in het aantal zonnebloem- en margaritische bloemenblaadjes, evenals in talloze patronen waarin planten hun bladeren hebben.

Kan u van dienst zijn: ordinale variabele

Experts zeggen dat planten op deze manier de ruimte voor bladeren en bloemen optimaliseren om een ​​optimale groei te hebben.

Met een centraal punt als startplaats groeien deze structuren en ontvangen ze zonlicht, daarom moeten de nieuwe bladeren en bloemblaadjes zo weinig mogelijk dekken die eerst uitkwamen. En de beste manier om dit te bereiken is om een ​​groeipatroon aan te nemen in termen van de Fibonacci -reeks.

Fibonacci's opvolging bij dieren

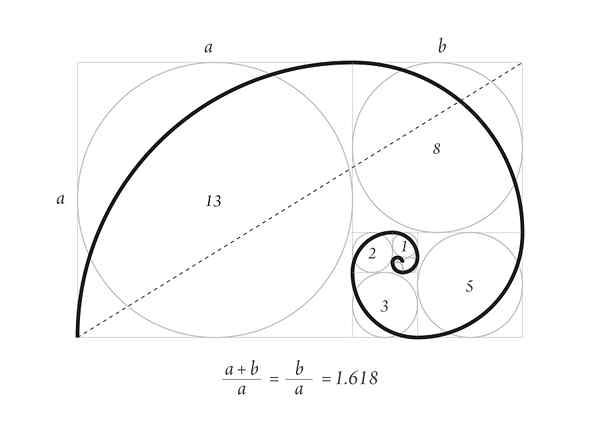Durero's spiraal met het eerste aantal opvolging van Fibonacci

De duurzame spiraal van het superieure beeld maakt deel uit van het groeipatroon van de schelpen bij zeedieren en de hoorns van sommige herkauwers.

Begin met twee vierkanten 1, één op de andere, dan een vierkant van zij 2 ernaast, dat een rechthoek van zij 3 vormt, waarvan de zijkanten de gouden verhouding hebben.

Hieronder is een vierkant van zij 3 en links een vierkant van zij 5. Boven is er een vierkant van zij 8 en rechts een vierkant van zij 13. Dit zijn de eerste nummers van de opvolging.

Eindelijk wordt de spiraal getrokken door de punten van de hoeken van de vierkanten aan te raken, zoals te zien in de figuur.

Toepassingen

De opvolging van Fibonacci wordt op verschillende gebieden toegepast:

-In de kunst verschijnt de gouden verhouding die verband houdt met de opeenvolging van Fibonacci bij mensen en dingen die worden vertegenwoordigd door grote kunstenaars zoals Leonardo da Vinci, Miguel Ángel en Alberto Durero.

-De verhoudingen van de partner in Athene reageren ook op het goudnummer.

-In de composities van Mozart, Beethoven, Schubert en Debussy.

-Om objecten te ontwerpen waarvan de verhoudingen er harmonieus uitzien voor menselijke ogen, zoals creditcards, containers, vlaggen.

-Op de aandelenmarkt wordt het gebruikt om te voorspellen welke prijzen zijn trend terugkeert.

Referenties

1. Fibonacci -opvolging. Hersteld van: blogeducastur.is.
2. Stewart, J. 2007. Voorzetting. 5e. Editie. Cengage leren.
3. Vargas, m. Fibonacci opvolgingstoepassingen. Hersteld van: Matesup.Klet.
4. Wikipedia. Fibonacci -nummer. Opgehaald uit: in.Wikipedia.borg.