Halve cirkel hoe het perimeter, gebied, zwaartepunt, oefeningen te berekenen

Hij halve cirkel Het is een platte figuur gescheiden door een diameter van de omtrek en een van de twee platte cirkelvormige bogen bepaald door die diameter.

Op deze manier wordt een halve cirkel begrensd door een halve circumferentie, die bestaat uit een platte cirkelvormige boog en een recht segment dat zich bij de uiteinden van de platte cirkelvormige boog verbindt. De halve cirkel bedekt de halve cirkel en alle interieur wijst op hetzelfde.

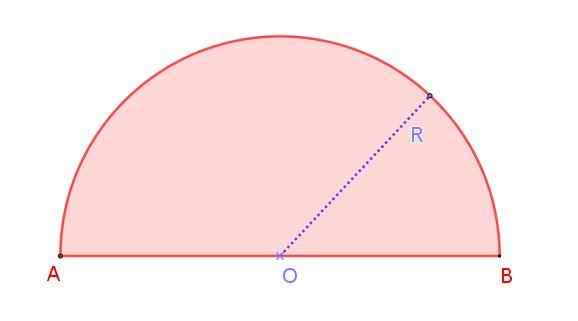
Figuur 1. Radio R Radio Semicircle. Bron: f. Zapata.

We kunnen dit zien in figuur 1, die een radio r rión r toont, waarvan de maat de helft van de diameter AB is. Merk op dat in tegenstelling tot een cirkel, waarin er oneindige diameters zijn, er in de halve cirkel slechts één diameter is.

De halve cirkel is een geometrische figuur met veel toepassingen in architectuur en ontwerp, zoals we in de volgende afbeelding zien:

Figuur 2. Seminicírculo als een decoratief element in de architectuur. Bron: Pikist.

[TOC]

Elementen en maatregelen van een halve cirkel

De elementen van een halve cirkel zijn:

1.- De platte cirkelvormige boog A⌒b

2.- Het segment [AB] 

3.- Het interieur wijst op halve cirkel samengesteld uit de A⌒b -boog en segment [AB].

Omtrek van een halve cirkel

De omtrek is de som van de contour van de boog plus die van het rechte segment, daarom:

Perimeter = booglengte A⌒b + segmentlengte [ab]

In het geval van een radio -halve cirkel r zal de perimeter P door de formule worden gegeven:

P = π⋅r + 2⋅r = (π + 2) ⋅r

De eerste term is de helft van de omtrek van een straal R -omtrek, terwijl de tweede de lengte van de diameter is, die twee keer de straal is.

Kan u van dienst zijn: thermometrische schalen

Gebied van een halve cirkel

Aangezien een halve cirkel een van de vlakke hoeksectoren is die overblijven door een diameter door de omtrek te tekenen, zal het gebied A de helft van het cirkelgebied zijn dat de radio semicircle r:

A = (π⋅r²) / 2 = ½ π⋅r²

Zwaartepunt van een halve cirkel

Het zwaartepunt van een halve cirkel bevindt zich op zijn symmetrieas tot een hoogte gemeten uit zijn diameter van 4/(3π) maal de straal r.

Dit komt overeen met ongeveer 0,424⋅R, gemeten vanuit het midden van de halve cirkel en op zijn symmetrieas, zoals getoond in figuur 3.

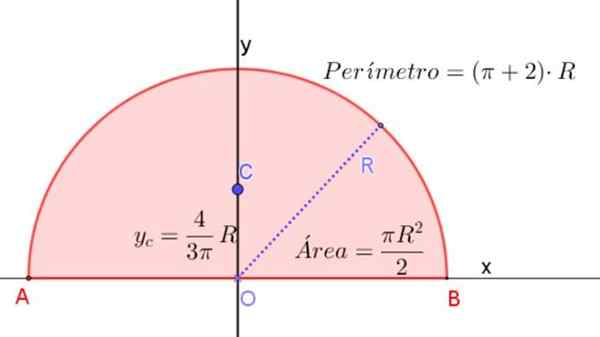figuur 3. Halve cirkel van radio R, wat de formules aangeeft om het gebied, perimeter en locatie van zijn centroid te bepalen. Bron: f. Zapata.

Moment van traagheid van een halve cirkel

Het traagheidsmoment van een platte figuur wordt gedefinieerd met betrekking tot een as, bijvoorbeeld X -as, zoals:

De integrale van het kwadraat van de afstand van de punten die tot de figuur tot de as behoren, waarbij het integratiedifferentieel een oneindig gebied van gebied is, genomen in de positie van elk punt. 

Figuur 4 toont de definitie van het traagheidsmoment i_X van de halve cirkel van Radio R, met betrekking tot de X -as die door zijn diagonaal gaat:

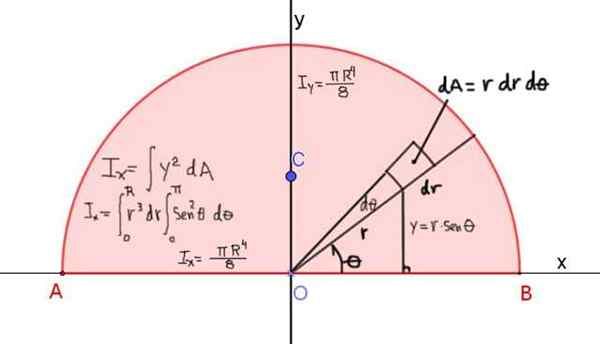Figuur 4. Definitie van het traagheidsmoment van een halve cirkel met betrekking tot de X -as die door zijn diagonaal gaat. Het resultaat wordt getoond voor de traagheidsmomenten ten opzichte van de X- en Y -assen. Bron: f. Zapata.

Het traagheidsmoment ten opzichte van de X -as wordt gegeven door:

Je_X = (π⋅r⁴) / 8

En het traagheidsmoment ten opzichte van de symmetrieas en is:

Kan u van dienst zijn: golvende optica

Iy = (π⋅r⁴) / 8

Het laat zien dat beide traagheidsmomenten samenvallen in hun formule, maar het is belangrijk om te benadrukken dat ze naar verschillende assen worden verwezen.

Geregistreerde hoek

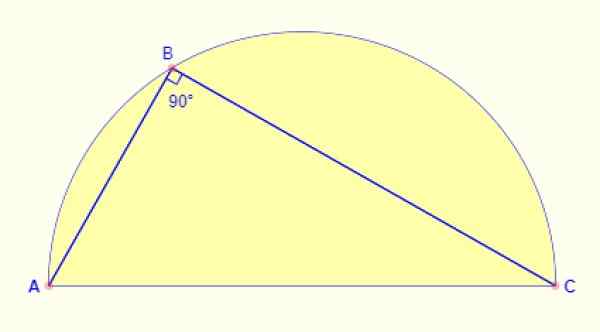
De hoek geregistreerd in de halve cirkel is altijd 90º. Ongeacht welk deel van de boog tot het punt wordt gebracht, de hoek die wordt gevormd tussen zijkanten AB en BC van de figuur is altijd recht.

Figuur 5. Hoek geregistreerd in de halve cirkel. Bron: Math Open Referentie.

Opgeloste oefeningen

Oefening 1 

Bepaal de perimeter van een halve cirkel van 10 cm straal.

Oplossing

Bedenk dat de perimeter afhankelijk van de straal wordt gegeven door de formule die we eerder hebben gezien:

P = (2 + π) ⋅r

P = (2 + 3.14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Oefening 2

Vind het gebied van een radio -halve cirkel van 10 cm.

Oplossing

De formule voor het gebied van een halve cirkel is:

A = ½ π⋅r² = ½ π⋅ (10 cm)² = 50π cm² = 50 x 3,14 cm² = 157 cm².

Oefening 3

Bepaal de hoogte h van het zwaartepunt van een straal halve cirkel r = 10 cm gemeten vanaf de basis, hetzelfde is de diameter van de halve cirkel. 

Oplossing

Het zwaartepunt is het halve cirkel -evenwichtspunt en de positie is op de symmetrieas op een hoogte h van de basis (halve cirkel diameter):

H = (4⋅r) / (3π) = (4⋅10 cm) / (3 x 3.14) = 4,246 cm

Oefening 4

Vind het traagheidsmoment van een halve cirkel met betrekking tot de as die samenvalt met zijn diameter, wetende dat de halve cirkel van een dun vel is gemaakt. De straal is 10 cm en de massa is 100 gram.

Oplossing

De formule die het traagheidsmoment van de halve cirkel geeft, is:

Kan u van dienst zijn: Solid State Fysica: eigenschappen, structuur, voorbeelden

Je_X = (π⋅r⁴) / 8

Maar omdat het probleem ons vertelt dat het een materiële hal.

Je_X = σ (π⋅r⁴) / 8

We bepalen vervolgens σ, wat niets anders is dan de massa van de halve cirkel verdeeld tussen het gebied van hetzelfde.

Het gebied werd bepaald in Oefening 2 en het resultaat was 157 cm². Dan zal de oppervlakkige dichtheid van deze halve cirkel zijn:

σ = 100 gram / 157 cm² = 0,637 g/cm²

Dan wordt het traagheidsmoment ten opzichte van de diameter als volgt berekend:

Je_X = (0,637 g/cm²) [3.1416 ⋅ (10 cm)⁴]/ 8

Resulterend:

Je_X = 2502 g⋅cm²

Oefening 5

Bepaal het traagheidsmoment van een radius halve cirkel 10 cm gebouwd van een materiaalplaat met een oppervlaktedichtheid van 0,637 g/cm² door een as die door zijn zwaartepunt gaat en parallel is aan zijn diameter.

Oplossing

Om deze oefening op te lossen, is het noodzakelijk om de stelling van Steiner te onthouden op momenten van traagheid van parallelle assen, die zegt:

Het moment van traagheid I ten opzichte van een as die zich op afstand van het zwaartepunt bevindt, is gelijk aan de som van het traagheidsmoment I_C Met betrekking tot een as die door het zwaartepunt gaat en parallel is aan de eerste, meer het product van het deeg door het kwadraat van de scheiding van de twee assen.

I = i_C + M h²

In ons geval is het bekend dat het het moment van traagheid is met betrekking tot de diameter, die al was berekend in Oefening 4. H weet ook tussen de diameter en de zwaartepunt, die werd berekend in Oefening 3.

We moeten gewoon IC wissen:

Je_C = I - M H²

Je_C = 2502 g⋅cm² - 100 g ⋅ (4.246 cm)² resulterend in het traagheidsmoment door een as parallel aan de diameter en die door het zwaartepunt gaat, is: 

Je_C = 699.15 g⋅cm²

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Math Open Referentie. Halve cirkel. Hersteld van: Mathpenref.com.
3. Universe -formules.Halve cirkel. Hersteld van: UniversOFormulas.com.
4. Universe -formules. Gebied van een halve cirkel. Hersteld van: UniversOFormulas.com.
5. Wikipedia. Halve cirkel. Opgehaald uit: in.Wikipedia.com.