Storgen regel

We leggen uit wat de storing -regel is, de toepassing ervan en geef verschillende voorbeelden

Wat is de storing -regel?

De Storgen regel Het is een criterium dat wordt gebruikt om het aantal klassen of intervallen te bepalen dat nodig is om een ​​reeks statistische gegevens grafisch te laten lijken. Deze regel werd in 1926 vermeld door de Duitse wiskundige Herbert Sturges.

Sturges stelde een eenvoudige methode voor, gebaseerd op het aantal X -monsters waarmee het aantal klassen en hun bereik van het bereik mogelijk was. Sturges -regel wordt vooral op grote schaal gebruikt in het statistische gebied, met name om frequentiehistogrammen te bouwen.

Uitleg

De storingregel is een empirische methode die veel wordt gebruikt in beschrijvende statistieken om het aantal klassen te bepalen dat moet bestaan ​​in een frequentiehistogram, om een ​​set gegevens te classificeren die een steekproef of populatie vertegenwoordigen.

Kortom, deze regel bepaalt de breedte van grafische containers, frequentiehistogrammen.

Om de regel vast te stellen, beschouwde Herbert Sturges een ideaal frequentiediagram, dat bestaat uit k -intervallen, waarbij het i -dit interval een bepaald aantal monsters bevat (i = 0, ... k - 1), weergegeven als:

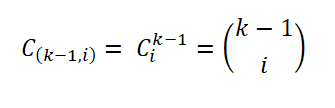
Dit aantal monsters wordt gegeven door het aantal manieren waarop een subset van een set kan worden geëxtraheerd; dat is, door de binomiale coëfficiënt, als volgt uitgedrukt:

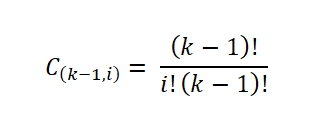Vervolgens verbonden storing dat het frequentiehistogram een ​​normale verdeling zal benaderen wanneer het aantal intervallen (k) toeneemt volgens de centrale stelling van de limiet. Op een zodanige manier dat het aantal monsters van elk van de intervallen kan worden berekend:

Het kan u van dienst zijn: Enegon: Eigenschappen, hoe u een enegon kunt maken, voorbeelden

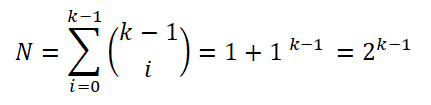
Om de uitdrukking te vereenvoudigen, paste hij de eigenschappen van logaritmen in beide delen van de vergelijking toe:

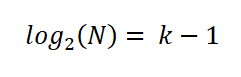
Sturges stelde dus vast dat het optimale aantal K -intervallen door de uitdrukking wordt gegeven:

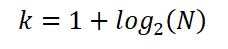
Het kan ook worden uitgedrukt als:

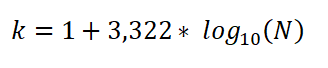
In deze uitdrukking:

• K is het aantal klassen.
• N is het totale aantal waarnemingen in de steekproef.
• Log is de gemeenschappelijke basislogaritme 10.

Om bijvoorbeeld een frequentiehistogram uit te werken dat een willekeurige steekproef van de gestalte van 142 kinderen tot expressie brengt, is het aantal intervallen of klassen die de verdeling zal hebben:

K = 1 + 3,322 _* aanroepen₁₀ (N)

K = 1+3,322_* Log (142)

K = 1+3,322_* 2.1523

K = 8.14 ≈ 8

De verdeling zal dus in 8 intervallen zijn.

Het aantal intervallen moet altijd worden weergegeven door hele getallen. In gevallen waarin de waarde decimaal is, moet een benadering worden gemaakt bij het dichtstbijzijnde gehele nummer.

Sturges -regeltoepassingen

De storingregel wordt voornamelijk toegepast in statistieken, omdat het een frequentieverdeling mogelijk maakt door de berekening van het aantal klassen (k), evenals de lengte van elk van deze, ook bekend als amplitude.

De amplitude is het verschil in de bovenste en ondergrens van de klasse, gedeeld door het aantal klassen, en wordt uitgedrukt:

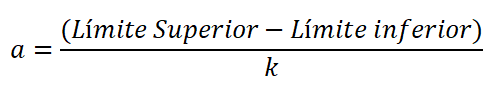
Er zijn veel empirische regels die een frequentieverdeling mogelijk maken. De storingregel wordt echter vaak gebruikt omdat het een benadering van het aantal klassen maakt, dat meestal van 5 naar 15 gaat.

Op deze manier beschouwt het een waarde die een steekproef of populatie goed vertegenwoordigt; Dat wil zeggen, de aanpak vertegenwoordigt geen extreme groepen, noch werkt het met een buitensporig aantal klassen die niet toestaan ​​het monster samen te vatten.

Het kan u van dienst zijn: tegenovergestelde hoeken door het hoekpunt (met een opgeloste oefening)

Voorbeeld

Een frequentiehistogram moet worden uitgevoerd volgens de gegeven gegevens, die overeenkomen met leeftijden verkregen in een onderzoek onder mannen die in een lokale gymnasium sporten.

Om de intervallen te bepalen, moet de steekproefomvang of het aantal waarnemingen bekend zijn; In dit geval zijn er 30.

Dan is de storing -regel van toepassing:

K = 1 + 3,322 _* aanroepen₁₀ (N)

K = 1+3,322_* Log (30)

K = 1+3,322_* 1.4771

K = 5,90 ≈ 6 intervallen.

Uit het aantal intervallen kunt u de amplitude berekenen die ze zullen hebben; dat wil zeggen, de breedte van elke balk weergegeven in het frequentiehistogram:

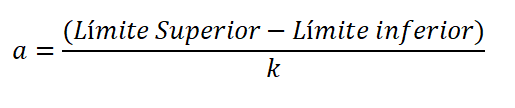
De ondergrens wordt beschouwd als de lagere waarde van de gegevens, en het bovenste is de hoogste waarde. Het verschil tussen de bovenste en ondergrens wordt het bereik of de route van de variabele genoemd (R).

De tabel heeft dat de bovengrens 46 is en de onderste 13; Op die manier zal de amplitude van elke klasse zijn:

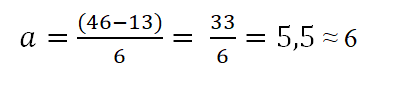
De intervallen zullen bestaan ​​uit een bovenste en ondergrens. Om deze intervallen te bepalen, begint het met het tellen van de ondergrens, waardoor de amplitude wordt bepaald door regel (6), als volgt:

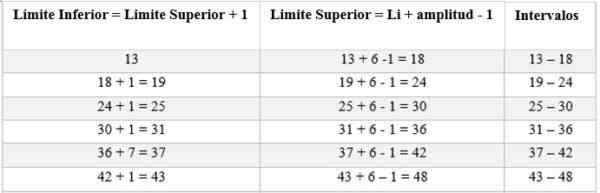
Vervolgens wordt de absolute frequentie berekend om het aantal mannen te bepalen dat overeenkomt met elk interval; In dit geval is het:

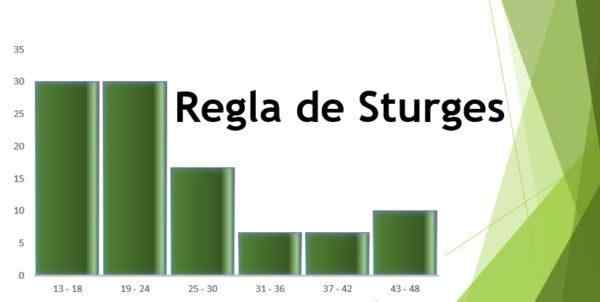
• Interval 1: 13 - 18 = 9
• Interval 2: 19 - 24 = 9
• Interval 3: 25 - 30 = 5
• Interval 4: 31 - 36 = 2
• Interval 5: 37 - 42 = 2
• Interval 6: 43 - 48 = 3

Door de absolute frequentie van elke klasse toe te voegen, moet dit gelijk zijn aan het totale aantal van het monster; In dit geval, 30.

Kan u van dienst zijn: negatieve homotecia

Vervolgens wordt de relatieve frequentie van elk interval berekend, waardoor de absolute frequentie hiervan wordt gedeeld door het totale aantal waarnemingen:

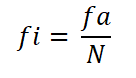
• Interval 1: fi = 9 ÷ 30 = 0,30
• Interval 2: fi = 9 ÷ 30 = 0,30
• Interval 3: fi = 5 ÷ 30 = 0.1666
• Interval 4: fi = 2 ÷ 30 = 0,0666
• Interval 5: fi = 2 ÷ 30 = 0,0666
• Interval 4: fi = 3 ÷ 30 = 0,10

Vervolgens kunt u een tabel maken die de gegevens weerspiegelt, en ook het diagram uit de relatieve frequentie in relatie tot de verkregen intervallen, zoals te zien in de volgende afbeeldingen:

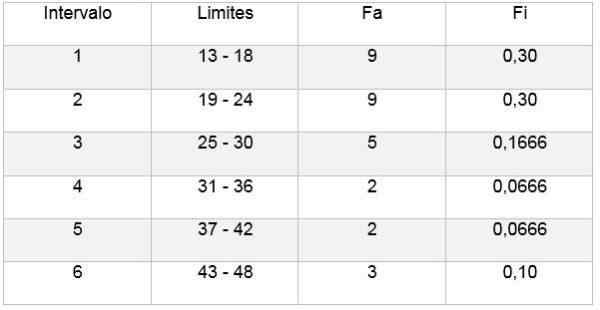
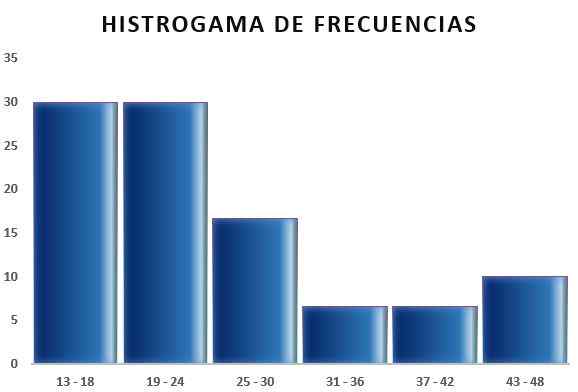
Op deze manier maakt de storingregel het mogelijk om het aantal klassen of intervallen te bepalen waarin een monster kan worden verdeeld, om een ​​gegevensmonster samen te vatten door de uitwerking van tabellen en afbeeldingen.