Gebied van een gewone en onregelmatige Pentagon hoe het wordt genomen, oefeningen

Om de Gebied van een Pentagon Eerst moeten we bepalen of dit regelmatig is of niet. Een Pentagon is een polygoon, een gesloten platte figuur van vijf zijden. Wanneer een polygoon regelmatig is, betekent dit dat de lengte van zijn zijden hetzelfde is en ook zijn interne hoeken.

In dat geval is er een formule om het exacte gebied van de reguliere polygoon te berekenen, wetende enkele van de belangrijkste kenmerken, die we later zullen afleiden.

Twee pentagons

Als de polygoon niet regelmatig is, dat wil zeggen, heeft het zijden van verschillende grootte en ongelijke interne hoeken, er is geen enkele formule.

Wiskundigen hebben echter berekeningsstrategieën gevonden, zoals het verdelen van de figuur in anderen met het laagste aantal zijden, zoals driehoeken, vierkanten en rechthoeken, waarvan de afmetingen bekend zijn of gemakkelijk worden berekend.

Een andere procedure om in het algemeen gebieden van polygonen te berekenen, wetende dat de coördinaten van zijn hoekpunten worden genoemd, is de methode die wordt genoemd Gauss -determinanten, die we later zullen beschrijven.

[TOC]

Hoe het gebied van een gewone Pentagon te berekenen?

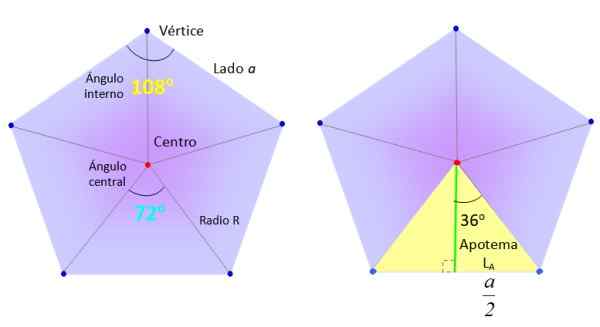
We gaan een normaal Pentagon van zij A nemen, en we zullen het verdelen in 5 gelijke driehoeken zoals weergegeven in de figuur, segmenten van het midden (rood) naar de hoekpunten (blauw) tekenen (blauw).

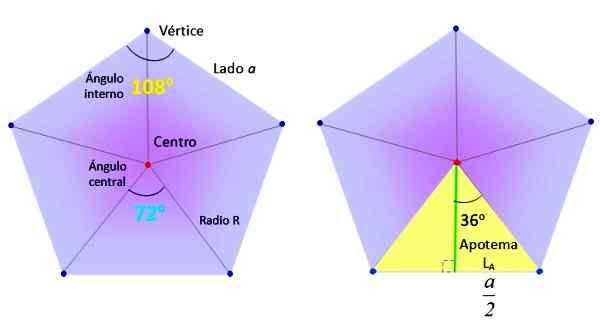De benodigde elementen om het reguliere Pentagon -gebied te vinden. Bron: f. Zapata.

Op zijn beurt zijn de driehoeken, zoals het uitstekende geel aan de rechterkant in de bovenste figuur, verdeeld in twee gelijke rechthoeken, dankzij het groene segment, genaamd Apothem.

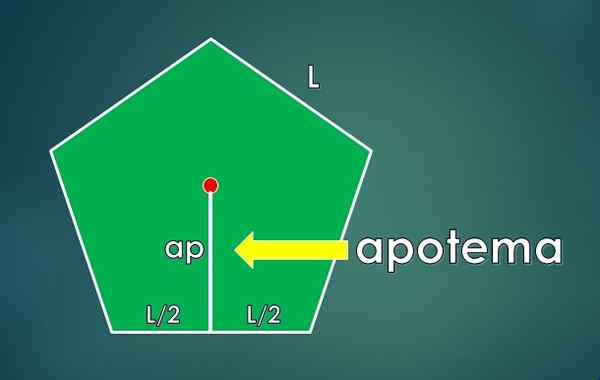
Apotheme wordt gedefinieerd als het loodrechte segment dat met het midden van één kant verbindt met het midden van de polygoon. De lengte is L_NAAR.

Het gebied van een rechthoekige driehoek van basis A/2 en hoogte L_NAAR is:

[(A/2) x l_NAAR]

Het Pentagon heeft 10 driehoeken zoals deze, daarom is het gebied:

Kan u van dienst zijn: vectorfuncties

A = 10 (a/2) x l_NAAR

Maar de omtrek P van het Pentagon is precies p =10 A, Daarom wordt het gebied gegeven door het semi -product van de omtrek en de lengte van de apothem:

A = P X L_NAAR /2

Regelmatig Pentagon -gebied ken

De lengte van de apothem l_NAAR Afhankelijk van de zijde A, wetende dat de aangegeven hoek de helft van de centrale hoek is, dat is 36º, equivalent aan:

36º = π/5

Door elementaire trigonometrie, door raaklijn van de acute hoek 36º:

Tan (π/5) = (a/2) ÷ l_NAAR

Vandaar:

L_NAAR=  (A/2) ÷ tan (π/5)

Vervangen in het gebied in mindering gebracht in de vorige sectie, en wetende dat p = 5a:

A = P X L_NAAR /2

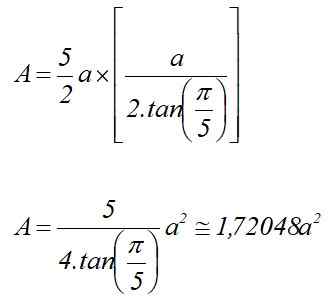
Regelmatig Pentagon -gebied kennende radio

Hij radio van een gewone polygoon is het segment dat van het midden naar een van de hoekpunten gaat. Het valt samen met de straal van de omschreven omtrek, zoals getoond in de volgende figuur:

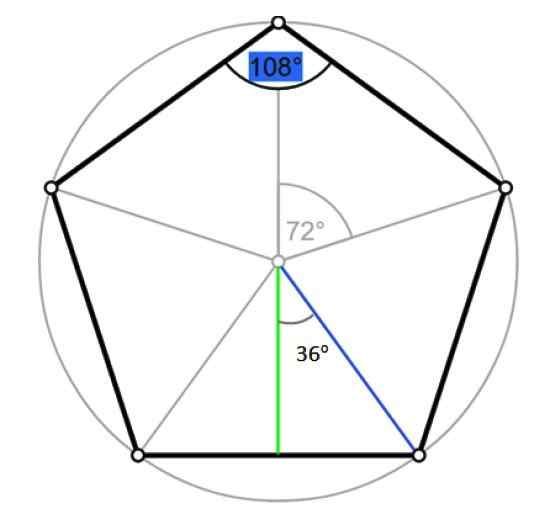Hoeken en apothem van het Pentagon. Bron: Wikimedia Commons/F. Zapata.

Laat R de maat zijn van genoemde radio, die samenvalt met de hypotenusa van de rechter driehoek die in de vorige figuur wordt afgebakend, in blauw. Door trigonometrie:

cos 36º = cos (π/5) = l_NAAR ÷ r

EN

sin 36º = sin (π/5) = (a/2) ÷ r

Daarom:

A = P X L_NAAR /2 = 5r. sin (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]

De formule met dubbele hoek gebruiken:

sin (2θ) = 2 sen θ . Cos θ

We moeten:

[sin (π/5) x cos (π/5)] = (1/2) sin 72º

En dus, door deze waarde te vervangen, verkrijgen we de volgende formule voor het reguliere Pentagon -gebied:

A = (5/2) r².Sen 72º

Hoe het gebied van een onregelmatig Pentagon te berekenen?

Zoals we al eerder hebben gezegd, is er voor een onregelmatige polygoon geen enkele formule, maar er zijn twee methoden die meestal heel goed werken, de eerste wordt triangulatie genoemd en de tweede is de methode van Gauss -determinanten.

Kan u van dienst zijn: bestaan ​​en uniekheid Stelling: demonstratie, voorbeelden en oefeningen

Triangulatie

Het bestaat uit het verdelen van de figuur in driehoeken, waarvan het gebied gemakkelijker te berekenen is of kan ook worden getest met andere figuren waarvan het gebied bekend is, zoals vierkanten, rechthoeken en trapezides.

Gauss -determinanten

Een andere manier om het onregelmatige Pentagon -gebied of een andere onregelmatige polygoon te vinden, is het plaatsen van de figuur in een Cartesiaans coördinatensysteem, om de coördinaten van de hoekpunten te vinden.

Bekend deze coördinaten, wordt de Gauss Determinants -methode toegepast om het gebied te berekenen, dat wordt gegeven door de volgende formule:

Waar a het gebied van de polygoon is en (x_N , En_N ) zijn de coördinaten van de hoekpunten. Een polygoon van N -zijden heeft 5 hoekpunten, voor het Pentagon zou het n = 5 zijn:

De balken die de formule vergezellen, zijn modulebars of absolute waarde.

Dit betekent dat hoewel het resultaat van de bewerking negatief is, we het moeten uitdrukken met een positief teken, en als het al positief is, moet het bij dat teken worden achtergelaten. Dit komt omdat een gebied altijd een positief bedrag is.

De procedure wordt Gauss -determinanten genoemd door zijn maker, de Duitse wiskundige Carl F. Gauss (1777-1855). De aangegeven bewerkingen zijn equivalent aan de bepalende factor van een 2 × 2 -matrix, bijvoorbeeld de eerste determinant is:

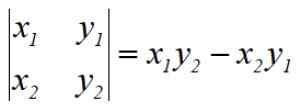
Om het Pentagon -gebied te vinden, moeten we 5 determinanten oplossen, het resultaat algebraïsch toevoegen, het delen door 2 en uiteindelijk het gebied uitdrukken altijd met een positief teken.

Opgeloste oefeningen

Oefening 1

Zoek het reguliere Pentagon -gebied waarvan de apothem 4 cm waard is en waarvan de kant 5 meet 5.9 cm.

Oplossing

Omdat het een normaal Pentagon is en we de maat voor de zijde en de apothem hebben, gebruiken we de eerder afgetrokken formule:

Kan u van dienst zijn: Scaleno Triangle

A = P X L_NAAR /2

Perimeter P is gelijk aan 5a = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Oefening 2

Zoek het getoonde onregelmatige Pentagon -gebied. De volgende dimensies zijn bekend:

DC ≈ van

AE = AB = 5

BC = 12

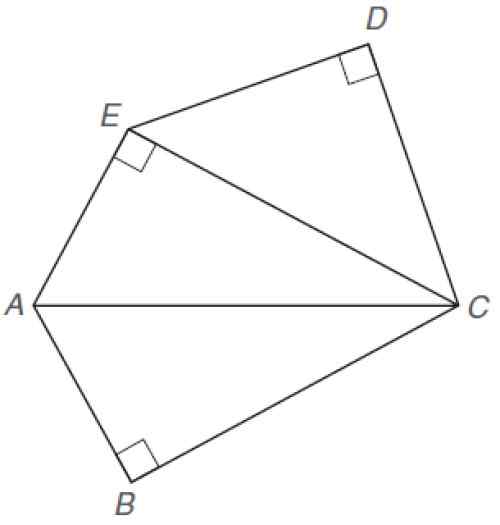Onregelmatig Pentagon. Bron: Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.

Oplossing

Het Pentagon -gebied is de som van de gebieden van de driehoeken, die rechthoeken zijn. De verklaring zegt dat DC ≈ van, daarom bij het toepassen van de Pythagoras -stelling op de EDC -driehoek, deze heeft:

EC² = 2 ed². Dan EC = √2.ED.

AEC- en ABC -driehoeken hebben een gemeenschappelijke hypotenuse, wat het AC -segment is, daarom:

Ea² + EC² = AB² + BC²

Aangezien EA en AB hetzelfde meten, wordt verkregen dat:

Ec = bc = √2.ED

Sinds BC = 12, dan ED = 12 / √2 = 8.485.

Met deze waarden zullen we het gebied van elke driehoek berekenen en ze aan het einde toevoegen.

EDC Triangle -gebied 

ED X DC /2 = 8.485² / 2 = 36

AEC Triangle -gebied 

Ea x ec / 2 = ea x √2.ED / 2 = 5 x √2. 8.485/2 = 30

ABC Triangle -gebied 

AB X BC / 2

Dan is het gezochte gebied:

5 x 12/2 = 30

Het is hetzelfde als die van Triangle AEC, omdat beide dezelfde maatregelen hebben.

Onregelmatig Pentagon -gebied

Ten slotte is het gevraagde gebied de som van de gebieden van de drie driehoeken:

A = 36 + 30 + 30 eenheden = 96 eenheden.

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Math Open Referentie. Polygoongebied. Hersteld van: Mathpenref.com.
3. Universe -formules. Gebied van een onregelmatig pentagon. Hersteld van: UniversOFormulas.com.
4. Universe -formules. Gebied van een gewone Pentagon. Hersteld van: UniversOFormulas.com.
5. Wikipedia. Pentagon. Hersteld van: is.Wikipedia.com.