Wat zijn Coplanares -vectoren? (Met opgeloste oefeningen)

De Coplanares vectoren o Coplanarios zijn degenen die op hetzelfde vliegtuig zijn opgenomen. Als je slechts twee vectoren hebt, zijn dit altijd couplet.

Als u drie of meer vectoren heeft, kan het zijn dat een van hen niet in hetzelfde vlak is als anderen, daarom kunnen ze niet worden beschouwd als coplanares. De volgende figuur toont een reeks coplanares aangeduid met vetgedrukte vectoren NAAR, B, C En D:

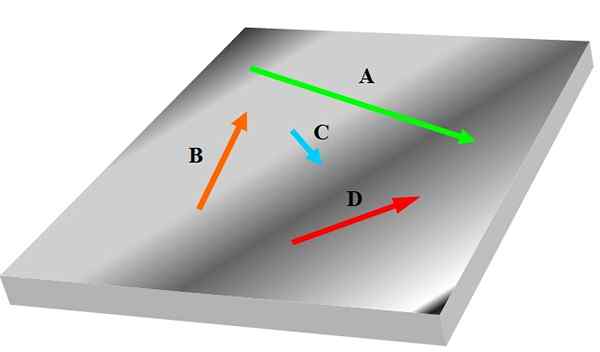Figuur 1. Vier coplanares. Bron: zelf gemaakt.

Vectoren zijn gerelateerd aan het gedrag en de eigenschappen van relevante fysieke magnitudes in wetenschap en engineering; Bijvoorbeeld snelheid, versnelling en kracht.

Een kracht produceert verschillende effecten op een object wanneer de manier waarop het wordt toegepast, wordt gevarieerd, bijvoorbeeld veranderende intensiteit, richting en betekenis. Nog steeds een van deze parameters wijzigen De resultaten zijn aanzienlijk verschillend.

In veel toepassingen, zowel in statische als dynamiek, zijn de krachten die op een lichaam werken op hetzelfde vlak, daarom worden ze beschouwd als coplanares.

[TOC]

Voorwaarden voor vectoren om coplanares te zijn

Voor drie vectoren om coplanares te zijn, moeten ze in hetzelfde vlak zijn en dit gebeurt als ze aan een van de volgende voorwaarden voldoen:

-Vectoren zijn parallel, daarom zijn hun componenten evenredig en zijn lineair afhankelijk.

-Uw gemengde product is nietig.

-Als je drie vectoren hebt en een van hen kan worden geschreven als een lineaire combinatie van de andere twee, zijn deze vectoren coplanares. Bijvoorbeeld een vector die het gevolg is van de som van twee anderen, de drie bevinden zich allemaal in hetzelfde vlak.

Kan u bedienen: voltmeter: kenmerken, werking, waarvoor is het, typen

Als alternatief kan de toestand van coplanariteit als volgt worden vastgesteld:

U v w Het zijn coplanares als er drie getallen (scalars) α, β, γ zijn zodanig dat αof + βv + γW = 0 Met (α, β, γ) verschillend van (0, 0, 0)

Gemengd product tussen drie vectoren

Het gemengde product tussen vectoren wordt gedefinieerd met drie vectoren of, v En W, resulterend in een scalaire die het gevolg is van het uitvoeren van de volgende bewerking:

of · ((v X W) = of · (v X W))

Eerst wordt het kruisproduct tussen haakjes gemaakt: v X W, waarvan het resultaat een normale (loodrechte) vector is naar het vlak waarin ze zo zijn v als W.

Ja of ligt op hetzelfde vlak als v En W, Natuurlijk moet het scalaire product (puntproduct) tussen u en genoemde normale vector 0 zijn. Op deze manier wordt geverifieerd dat de drie vectoren coplanares zijn (ze liggen op hetzelfde vlak).

Wanneer het gemengde product niet nul is, is het resultaat gelijk aan het volume van de parallellepiped die de vectoren heeft of, v En W als aangrenzende kanten.

Toepassingen

Coplanares, gelijktijdige en niet -colineale krachten

De sterke punten gelijktijdig Ze worden allemaal op hetzelfde punt toegepast. Als ze ook coplanares zijn, kunnen ze worden vervangen door slechts één, die wordt genoemd resulterende kracht En het heeft hetzelfde effect als dat van de oorspronkelijke krachten.

Als een lichaam in evenwicht is dankzij drie coplanares, gelijktijdige en niet -colineale (niet -parallelle) krachten, genaamd NAAR, B En C, Hij Lamy's stelling Hij wijst erop dat de relatie tussen deze krachten (magnitudes) als volgt is:

A / sin α = b / sen β = c / sen γ

Met α, β en γ als de hoeken die tegen de toegepaste krachten zijn, zoals getoond in de volgende figuur:

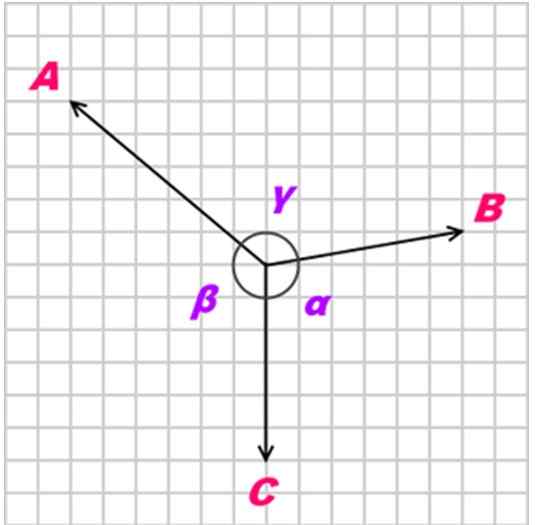Figuur 2. Drie krachten A, B en C Coplanares werken op een object. Bron: Kiwakwok bij Engelse Wikipedia [Public Domain]

Opgeloste oefeningen

-Oefening 1

Zoek de waarde van k zodat de volgende vectoren coplanares zijn:

Kan u van dienst zijn: Carnot Machine

of =

v =

W =

Oplossing

Aangezien de componenten van de vectoren worden gehouden, worden de criteria van het gemengde product daarom gebruikt:

of · ((v X W) = 0

Het wordt eerst opgelost v X W. De vectoren worden uitgedrukt in termen van de eenheidsvectoren Je, J En k Dat onderscheidt de drie loodrechte richtingen in de ruimte (breed, hoog en diepte):

v= 4 Je + J + 0 k

W= -1 Je + 2J -1 k

v X W = -4 (I x i) + 8 (I x J) - 4 (i x k) - (J X I) + 2 (J X J) - 2 (J x k) = 8 k + 4 J + K -2 i = -2 Je + 4 J + 9 k

Het scalaire product wordt nu voorgesteld tussen u en de vector die resultaten heeft van de vorige bewerking, bijpassende bewerking tot 0:

of · (v X W) = (-3 Je + k J + 2 k)) · (-2 Je + 4 J + 9 k) = 6 + 4K +18 = 0

24 + 4k = 0

De gezochte waarde is: k = - 6

Zodat de vector of is:

of =

-Oefening 2

De figuur toont een object waarvan het gewicht is W = 600 N, in evenwicht hangend dankzij de kabels die zijn geplaatst volgens de hoeken die worden getoond in figuur 3. Is het mogelijk om de stelling van Lamy in deze situatie toe te passen? Zoek in elk geval de grootte van T₁, T₂ En T₃ die evenwicht mogelijk maken.

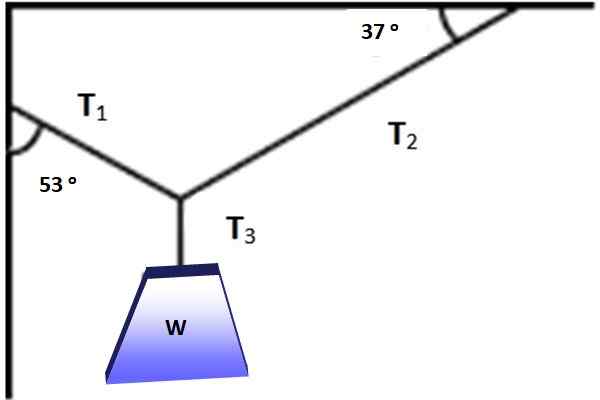figuur 3. Een gewicht hangt in evenwicht onder de werking van de drie getoonde spanningen. Bron: zelf gemaakt.

Oplossing

Lamy's stelling is van toepassing in deze situatie als de knoop waarop de drie spanningen worden toegepast, wordt overwogen, omdat ze een systeem van coplanar -krachten vormen. Eerst wordt het vrije lichaamsdiagram gemaakt voor het hanggewicht, om de grootte van T te bepalen_3:

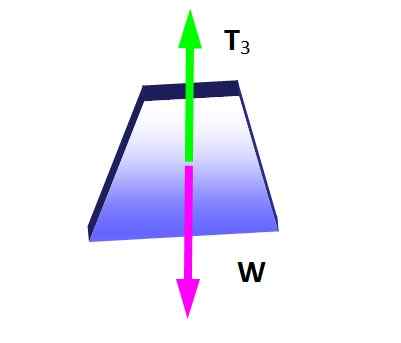Figuur 4. Gratis lichaamsdiagram voor het hangen van het gewicht. Bron: zelf gemaakt.

Uit de evenwichtsconditie volgt het dat:

Kan u van dienst zijn: diffractie van geluid: wat is voorbeelden, toepassingen

T₃  = W = 600 n

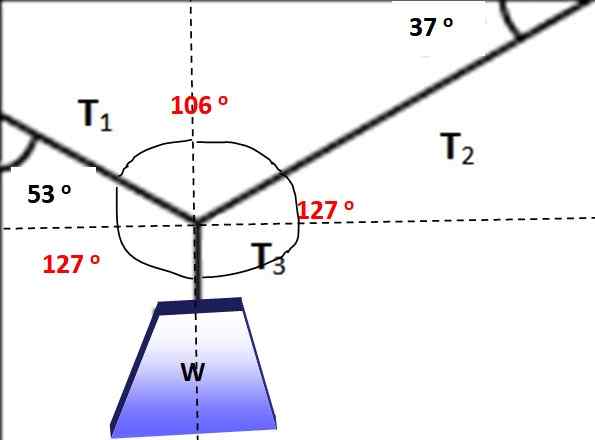
De hoeken tussen de krachten zijn in de volgende figuur in rood gemarkeerd, het kan gemakkelijk worden geverifieerd dat de som de som 360 ° is. Het is nu mogelijk om de stelling van Lamy toe te passen, omdat een van de krachten en de drie hoeken ertussen bekend is:

Figuur 5.- In rood de hoeken om de stelling van Lamy toe te passen. Bron: zelf gemaakt.

T₁ / Sen 127º = w / sen 106º

Daarom: T₁ = Sen 127º (w /sen 106º) = 498.5 n

Opnieuw wordt Lamy's stelling toegepast om T te wissen₂:

T₂ / sin 127 = t₁ / Sen 127º

T₂ = T₁ = 498.5 n

Referenties

1. Figueroa, D. Serie: Physics for Science and Engineering. Deel 1. Kinematica. 31-68.
2. Fysiek. Module 8: vectoren. Hersteld van: frtl.Utn.Edu.AR
3. Hibbeler, R. 2006. Mechanica voor ingenieurs. Statisch. 6e editie. Continentaal redactioneel bedrijf.28-66.
4. McLean, W. Schaum -serie. Mechanica voor ingenieurs: statisch en dynamisch. 3e editie. McGraw Hill. 1-15.
5. Wikipedia. Vector. Hersteld van: het is.Wikipedia.borg.