Wat de lengte van de verplaatsing van de zeshoek vertegenwoordigt

De zeshoek verplaatsingslengte vertegenwoordigt De lengte van de zijgezichten van het prisma. Om deze verklaring te begrijpen, is het eerste dat moet weten dat een zeshoek een polygoon is die uit zes kanten bestaat.

Dit kan regelmatig zijn, wanneer alle partijen dezelfde maatregel hebben; of het kan onregelmatig zijn, wanneer het ten minste één kant een andere maat heeft dan die van anderen.

Het belangrijkste dat moet worden opgemerkt, is dat er een zeshoek is en dit moet worden verplaatst, dat wil zeggen van plaats, langs een lijn die door het midden gaat.

Nu is de vraag wat de vorige verplaatsingslengte vertegenwoordigt? Een belangrijke observatie is dat de dimensies van de zeshoek er niet toe doen, alleen de lengte van zijn beweging is belangrijk.

Wat vertegenwoordigt verplaatsing?

Voordat u de vraag van de titel beantwoordt, is het handig om te weten wat de verplaatsing is gekoppeld aan de zeshoek.

Dat wil zeggen, het is gebaseerd op de veronderstelling dat er een gewone zeshoek is, en dit wordt een bepaalde lengte verplaatst, langs een lijn die door het midden gaat. Wat die verplaatsing genereert?

Indien in detail waargenomen, is te zien dat een zeshoekig prisma wordt gevormd. Het volgende cijfer illustreert deze kwestie beter.

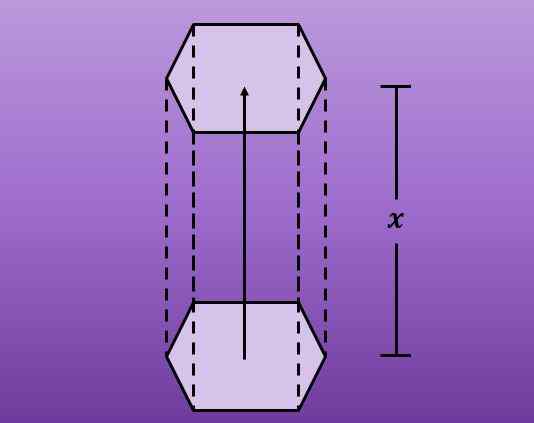
Wat de lengte van de verplaatsing vertegenwoordigt?

Volgens wat er is gezegd, genereert verplaatsing een zeshoekig prisma. En de vorige afbeelding detailleren, zie je dat de lengte van de verplaatsing van de zeshoek de lengte van de laterale gezichten van het prisma vertegenwoordigt.

Hangt de lengte af van de verplaatsingsrichting?

Het antwoord is nee. De verplaatsing kan met elke hellingshoek zijn en de lengte van de verplaatsing zal de lengte van de laterale gezichten van het zeshoekige prisma blijven vertegenwoordigen.

Als de verplaatsing wordt gedaan met een hellingshoek tussen 0 ° en 90 °, zal een schuine hexagonaal prisma worden gevormd. Maar dit verandert de interpretatie niet.

De volgende afbeelding toont de figuur verkregen door een zeshoek te verplaatsen langs een hellende lijn die door het midden gaat.

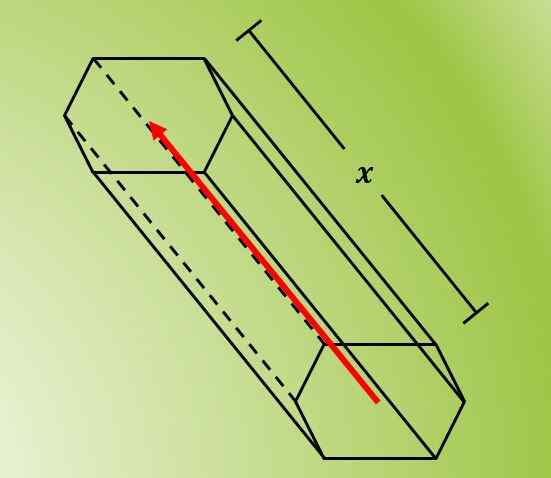
Nogmaals, de lengte van de verplaatsing is de lengte van de zijvlakken van de prisma.

Observatie

Wanneer de verplaatsing wordt gedaan langs een lijn loodrecht op de zeshoek en die door het midden gaat, valt de lengte van de verplaatsing samen met de zeshoekhoogte.

Met andere woorden, wanneer een recht zeshoekig prisma wordt gevormd, dan is de lengte van de verplaatsing de hoogte van de prisma.

Als de lijn integendeel een andere helling heeft dan 90 °, dan wordt de lengte van de verplaatsing de hypotenusa van een rechthoekige driehoek, waarbij een categorie van genoemde driehoek samenvalt met de hoogte van het prisma.

De volgende afbeelding laat zien wat er gebeurt als een zeshoek diagonaal weergeeft.

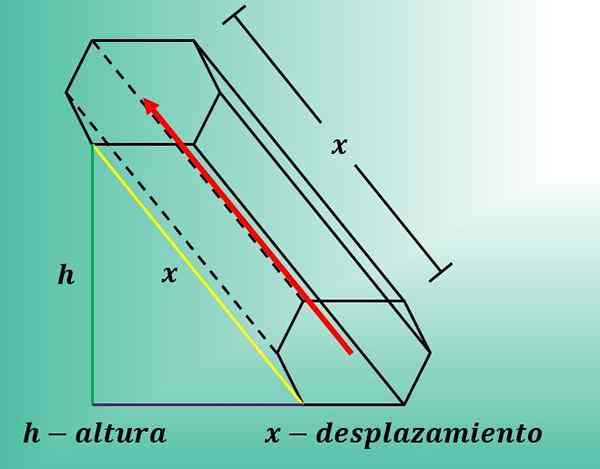
Ten slotte is het belangrijk om te benadrukken dat de afmetingen van de zeshoek de lengte van de verplaatsing niet beïnvloeden. 

Wat varieert is dat een recht of schuin zeshoekig prisma kan worden gevormd.