Wat is de relatie tussen de rhombus en het rechthoekige gebied?

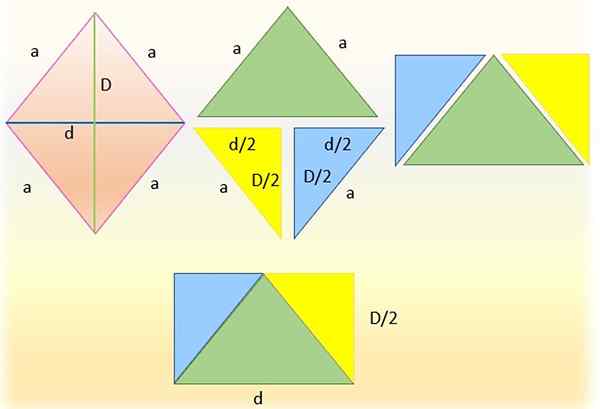
Een rhombus ontbinden om een ​​rechthoek te krijgen. Bron: f. Zapata

Het is mogelijk om het rhombusgebied (en enkele andere geometrische figuren) te berekenen uit het gebied van een driehoek of een gerelateerde vierhoek, zoals een parallellogram of een rechthoek.

Het rechthoek en het parallellogramgebied is hetzelfde: het wordt berekend als het product tussen de basis van de figuur en de hoogte ervan ten opzichte van die basis. Van zijn kant is het driehoeksgebied het semi -product tussen zijn basis en zijn hoogte.

Deze formules zijn gemakkelijk te onthouden, hoewel geometrie natuurlijk een exclusieve formule biedt voor het Rhombus -gebied, wetende de maat van de belangrijkste en kleine diagonalen, respectievelijk aangeduid als D en D:

Het is mogelijk om deze uitdrukking af te leiden door de volgorde van de bovenstaande figuur.

Om dit te doen, wordt de rhombus aan de linkerkant gesneden door een van zijn diagonalen, die werd gemaakt in de cijfer -secties door de kleine diagonaal, waardoor twee driehoeken worden verkregen. De bovenste driehoek (in groen) is achtergelaten en de onderste is op zijn beurt verdeeld in twee driehoeken, snijdt in de helft van de hoofddiagonaal, het verkrijgen van de driehoeken rechthoeken identiek blauw en geel.

Dan vallen de hypotenuses van deze driehoeken samen met de zijkanten van de groene driehoek, omdat ze hetzelfde meten, dat is "a". En een rechthoek wordt eindelijk verkregen, waarvan de basis de lagere "D" diagonaal is en waarvan de hoogte de helft is van de belangrijkste diagonaal, dat wil zeggen: "D/2".

Het aldus gevormde rechthoekige gebied valt precies samen dat van de rhombus, daarom kan worden bevestigd dat:

Kan u van dienst zijn: Trinomial

NAAR _diamant = (basis × hoogte) _rechthoek = D × (D/2)

Een resultaat dat, zoals te zien, precies samenvalt met de formule van het eerder gegeven Rhombus -gebied.

Rambo en parallellogramgebied

Het Rhombus -gebied is ook gerelateerd aan dat van een parallellogram, omdat beide geometrische figuren plat zijn en tot de familie van vierhuizen behoren. In de volgende afbeelding is er bijvoorbeeld een rhombus links en een parallellogram rechts.

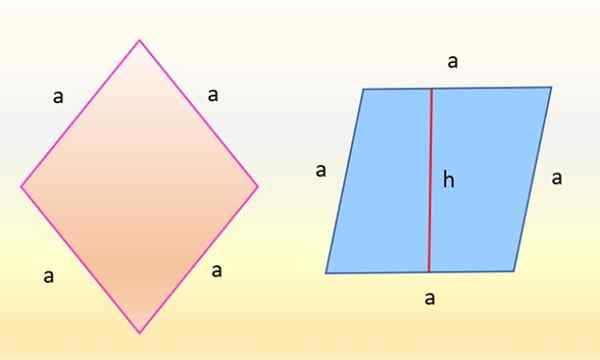Het rhombusgebied aan de linkerkant is hetzelfde als dat van het parallellogram rechts. Bron: f. Zapata

Het blijkt dat de cijfers identiek zijn, want wat is veranderd is alleen de oriëntatie. De rhombus aan de linkerkant, in roze, wiens zijden dezelfde maatregel hebben: a, het wordt zo veranderd dat een van zijn zijden volledig horizontaal is. Dan neemt de rhombus de vorm aan van het blauwe parallellogram aan de rechterkant.

En het gebied van dit parallellogram is ook het product tussen de basis "a" en de hoogte ten opzichte van die basis, "h" in de figuur genoemd: daarom:

NAAR _{parallellogram} = A × H

Omdat het dezelfde figuur is, is het gebied identiek en volgt dat:

NAAR _diamant = A × H

Dus weten en H van het parallellogram wordt het gebied berekend en zal het samenvallen met dat van de Rhombus.

Rombo -gebied ingeschreven in een rechthoek

Een andere relatie tussen Rhombus en rechthoek verschijnt wanneer de eerste is geregistreerd in de tweede. Als dit gebeurt, vallen de hoekpunten van de Rhombus samen met het middelpunt van de zijkanten van de rechthoek, die hieronder wordt weergegeven:

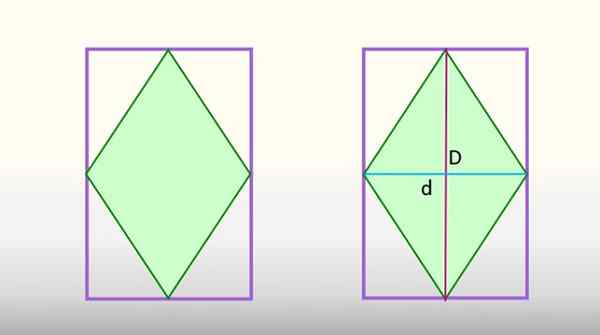Het rhombusgebied dat in de rechthoek is ingeschreven, is equivalent aan de helft van het rechthoekige gebied. Bron: f. Zapata

Deze bepaling maakt de belangrijkste en kleine diagonalen van de Rhombus, de figuur is verdeeld in 8 identieke driehoeken, waarvan 4 overeenkomen met de rhombus, in het groen, en de andere 4 maken deel uit van de rechthoek. Als deze laatste 4 driehoeken samenvoegen, zouden ze de helft van de rechthoek vormen, en de 4 Rhombus -driehoeken, de andere.

Het kan je van dienst zijn: Issmeles Triangle

Daarom is het Rhombus -gebied gelijk aan de helft van het rechthoekige gebied waarin het is geregistreerd, waarin staat dat:

NAAR_diamant = A_rechthoek / 2

Dit wordt gemakkelijk geverifieerd door het gebied van een van de driehoeken te berekenen en met 4 te vermenigvuldigen, omdat ze identiek zijn. Het gebied van elke driehoek is de helft van het product tussen de basis en de hoogte ervan:

NAAR _driehoek = Basis × Hoogte /2

Uit de vorige figuur wordt waargenomen dat de basis van een van de driehoeken d/2 is en de hoogte d/2 is, die vervangt in de vorige formule geeft:

NAAR _driehoek = (d /2) × (d /2) /2 = (d × d) /8

Dit resultaat vermenigvuldigen met 4 om het Rhombus -gebied te hebben:

NAAR _diamant = 4 (d × d) /8 = (d × d) /2

Van zijn kant is de helft van de rechthoek:

NAAR _rechthoek / 2 = basis × hoogte / 2

Aangezien de basis van de rechthoek D is en zijn hoogte is, blijft het:

NAAR_rechthoek / 2 = D × D/ 2

Dat is precies het gebied van de geregistreerde rhombus. Er wordt dan geconcludeerd dat:

Het gebied van een rhombus geregistreerd in een rechthoek is gelijk aan de helft van het gebied hiervan.

Opgeloste oefeningen

Oefening 1

Hoeveel is het rhombusgebied waarvan de belangrijkste diagonale meet 14.6 cm en de lagere diagonale 9.8 cm?

Oplossing

Door D = 14 te vervangen.6 cm en d = 9.8 cm in de Rhombus Area -formule:

Het gezochte gebied is:

NAAR _diamant = 14.6 cm × 9.8 cm = 143.1 cm²

Oefening 2

In de figuur van de voorgaande sectie is de belangrijkste diagonaal van de rhombus geregistreerd in de rechthoekige maatregelen d = 30 cm en het rechthoekige gebied is 210 cm waard². Er wordt gevraagd om te berekenen:

a) de lengte van de kleine diagonaal

Het kan u van dienst zijn: lijn- en semi -river -segment

b) Het rhombusgebied, op twee manieren: de eerste door het rechthoekige gebied en de tweede met behulp van de formule van het gebied van een rhombus. Controleer of het resultaat hetzelfde is.

Oplossing voor

Het rechthoekige gebied is het product tussen zijn basis en zijn hoogte. De grootste diagonaal is de hoogte, terwijl de kleinste diagonale D de basis zou zijn. Met behulp van de gebiedsformule en het vervangen van de waarden van de verklaring, hebt u:

NAAR _rechthoek = Base × Hoogte = D × 30 cm = 210 cm²

Dan is de basis waard:

D = 210 cm² / 30 cm = 7 cm

Oplossing B

Zoals hierboven te zien, is het Rhombus -gebied de helft van het rechthoekige gebied, en dit is bekend:

NAAR _diamant = 210 cm² /2 = 105 cm²

Het resultaat wordt onmiddellijk gecontroleerd en vervangt in de formule:

De diagonalen zijn al bekend: d = 30 cm, d = 7 cm, dan:

NAAR _diamant = 30 cm × 7 cm /2 = 105 cm²

Het is bewezen dat, zoals verwacht, het Rhombus -gebied in beide gevallen hetzelfde is.