Wat is de richtlijn? (Geometrie)

De richtlijn In geometrie bestaat het uit een curve, oppervlak of volume die vast blijft en bepaalt de manier waarop een geometrisch object wordt gevormd. Bijvoorbeeld, door een lijn zijn andere curven zoals conische, en revolutieoppervlakken, zoals de rechte cirkelvormige cilinder.

De richtlijncurve kan ook een omtrek zijn. Een rechte cirkelvormige cilinder kan worden gevormd door een straal ri -r rión ri achter te laten.

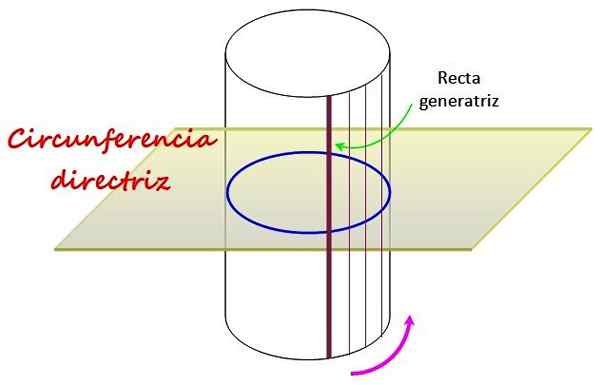
Figuur 1. Een rechte cirkelvormige cilinder heeft als leidraad een cirkel, waarrond een rechte lijn genaamd Generatrix beweegt. Bron: f. Zapata.

De omtrek, die in het vlak in de figuur is getrokken, bepaalt de vorm van het gebogen oppervlak van de rechte cirkelvormige cilinder, die wordt gegenereerd door de lijn eromheen te roteren, genoemd Rechte generatrix.

Als de begeleidingscurve geen omtrek is, maar een andere curve, worden andere soorten cilinder gegenereerd, zoals de elliptische cilinder, waarvan de richtlijn een ellips is.

Een omtrek kan ook fungeren als een richtlijn om een ​​andere curve te genereren, zo is het geval van de Epitrocoid, Een curve in het vlak gegenereerd door een punt, die op zijn beurt in een kleinere cirkel is die rolt zonder te glijden, rond de richtlijn.

Het is gemakkelijker om het visueel te waarderen door de volgende animatie:

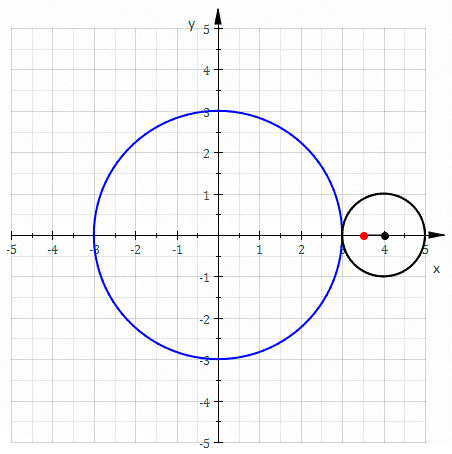Figuur 2. De rode curve wordt genoemd Epitrocide en zijn richtlijncurve. Bron: Wikimedia Commons. Sam Derbyshire op de Engelse Wikipedia/CC BY-S (http: // creativeCommons.Org/licenties/by-sa/3.0/).

De richtlijncurve op cilindrische oppervlakken

Cilindrische oppervlakken worden geclassificeerd volgens hun richtlijncurve in cilinders:

-Circulaire

-Elliptisch

-Parabolisch

-Hyperbolisch

Wanneer een cilindrisch oppervlak een richtlijn heeft die in een vlak loodrecht op dat van de generatrixlijn ligt, is de vergelijking van dit oppervlak dezelfde als de richtlijn van de richtlijn.

Het kan u van dienst zijn: wat is de relatie tussen het rhombusgebied en de rechthoek?

De cilinders behoren tot de groep van Kwadrische oppervlakken, wiens vergelijking de tweede klas is met drie variabelen. De algemene vorm is:

Bijl² + Door² + CZ² + Dxy + exz + fyz + gx + hy + iz + k = 0

Waar coëfficiënten A, B, C ... reële getallen zijn.

De cilinders zijn de meest voorkomende en nuttige drie -dimensionale geometrische lichamen die kunnen worden gevonden, vooral de rechte cirkelvormige cilinders, maar de andere soorten cilinders die hieronder worden beschreven, hebben ook toepassingen in engineering en ontwerp.

Rechte cirkelvormige cilinder

De richtlijn is een cirkel C die in een vlak loodrecht op de cilinder staat, zoals getoond in figuur 1, omdat de generatrixlijn, die naar C draait om het laterale oppervlak te vormen, loodrecht staat op C.

De vergelijking van omtrek C op het XY -vlak, gericht op de oorsprong (0.0) is:

X² + En² = R²

Waar r, de straal van de omtrek zal uiteraard de straal van de cilinder zijn. De hoogte H van de cilinder strekt zich uit langs de Z -as, loodrecht op het XY -vlak.

Elliptische cilinder

De richtlijn is een ellips in het XY -vlak gecentreerd op de oorsprong (0.0), waarvan de vergelijking is:

De generatrix is ​​een lijn loodrecht op het XY -vlak, dat rond de ellips beweegt om aanleiding te geven tot het laterale oppervlak. De ellips kan op elke hoogte Z op het XY -vlak zijn.

Bijvoorbeeld de vergelijking ellips:

4x² + 9y² = 36

Het is de richtlijncurve die aanleiding geeft tot de elliptische cilinder waarvan de vergelijking 4x is² + 9y² = 36, plus z = 0. Door deze laatste uitdrukking toe te voegen, is het duidelijk dat het het oppervlak is.

Kan u van dienst zijn: bemonsteringsfout: formules en vergelijkingen, berekening, voorbeelden

Parabolische cilinder

In dit geval is de richtlijn een gelijkenis, die kan zijn van de vorm y = x². Aldus wordt de cilinder gericht langs de Z -as en vormt het stapelen van gelijkenissen met een hoekpunt in (0,0) langs die as.

De parabolische cilinder heeft toepassing in zonne -energie, omdat sommige verzamelaars op die manier spiegels hebben, waardoor zonlicht geconcentreerd is in de focus. Dit punt passeert een rechte pijp waarbinnen een olie temperaturen bereikt tot 400 º C.

Hyperbolische cilinder

In de hyperbolische cilinder is de vergelijking van de richtlijn de hyperbool gecentreerd op de oorsprong:

De cilinder wordt gevormd aan de stapel.

Revolutieoppervlak

De richtlijncurve van een revolutieoppervlak is dezelfde as van revolutie, de lijn waarrond de curve die verantwoordelijk is voor het genereren van het oppervlak.

De curve die draait, kan een willekeurige vorm hebben, op deze manier wordt een gebied gegenereerd zoals te zien in deze animatie:

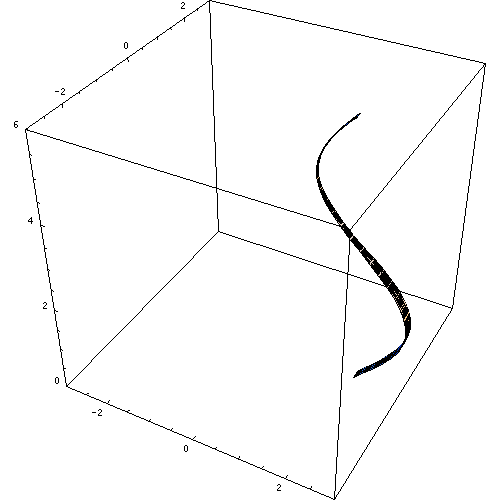figuur 3. Een revolutieoppervlak. Bron: Wikimedia Commons. https: // upload.Wikimedia.Org/wikipedia/commons/e/e7/rotationkoerper_animation.Gif.

Als een andere lijn om draait om de richtlijn, wordt de reeds bekende rechte cirkelcilinder verkregen. Op dezelfde manier kunnen andere revolutieoppervlakken worden verkregen, zoals conische, sferische en torusvormige revolutieoppervlakken.

Conisch oppervlak

Een conisch oppervlak wordt gegenereerd door beweging van een generatrixlijn die altijd door de vaste platte curve of richtlijncurve gaat en door het vaste punt genaamd vertex, dat niet tot het richtlijnvlak behoort.

Kan u van dienst zijn: Wiskundige hoop: formule, eigenschappen, voorbeelden, oefening

Het hoekpunt of de punt verdeelt de kegel in twee delen, genoemd bladeren of takken.

Opgeloste oefeningen

- Oefening 1

Zoek het laterale gebied van de hoge cirkelvormige cilinder van hoogte 25 cm, waarvan de richtlijncurve de straalomtrek van 6 cm is, gericht op de oorsprong.

Oplossing

Het laterale gebied van de cilinder is het product van de lengte van de richtlijn op hoogte. Als r de straal van de omtrek is en H de hoogte van de cilinder is, wordt het gebied gegeven door:

A = 2πr x h = 2πx 6 cm x 25 cm = 942.5 cm²

- Oefening 2

U hebt de volgende vergelijking die overeenkomt met een quadric -oppervlak:

X² + En² + 2z² +2xz - 2yz = 1

Geef aan welk oppervlak het is en wat de vergelijking van de richtlijn is.

Oplossing

Z = k doen, waarbij k constant is, wordt het verkregen:

X² + En² + 2k² +2kx - 2ky = 1

We herschikken de termen als volgt:

(X² + 2kx) + (en²- 2ky) = 1-2k²

Vierkanten moeten², Om geen van de haakjes te wijzigen:

(X² + 2kx + k² - k² ) + (en² - 2ky + k² - k²) = 1-2k²

(X² + 2kx + k²) - K²  + (En²- 2ky + k²) - K² = 1-2k²

Op deze manier blijft het:

(x + k)² + (en - k)² = 1

Zoals de vergelijking van een middelste cirkel (-k, k) en straal 1, is het oppervlak een rechte cirkelvormige cilinder, ook van radio 1, zolang de generatrixlijn loodrecht staat op de genoemde omtrek.

Bijvoorbeeld, met k = 0, wordt de vergelijking gereduceerd tot de omtrek gecentreerd op de oorsprong (0,0) waarvan de straal 1 is:

X² + En² = 1

Referenties

1. Gaussians. Vertegenwoordigen drie -dimensionale oppervlakken. Hersteld van: Gaussians.com.
2. Kindle, J. Theorie en problemen van analytische geometrie. McGraw Hill. Schaum -serie.
3. Oppervlakken als geometrische plaatsen. Hersteld van: algebra.FRLP.Utn.Edu.AR.
4. Suárez, m. Oppervlakken. Opgehaald uit: onderwerpen.Unq.Edu.AR.
5. Kwadrische oppervlakken. Hersteld van: systemen.fciencias.UNAM.mx.