Radicale eigenschappen

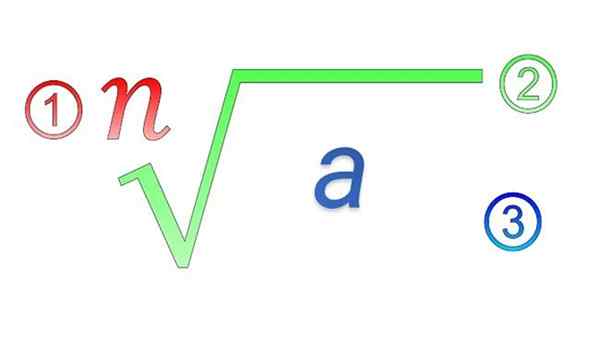
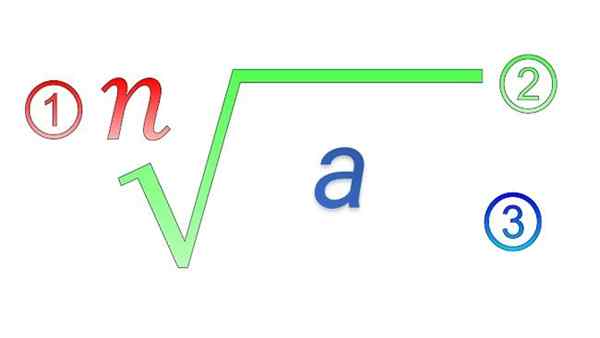Radicale elementen: 1) index; 2) radicaal symbool; 3) Subradicale hoeveelheid

Wat zijn de eigenschappen van de radicalen?

De radicale eigenschappen Het zijn operaties die complexe problemen van radicalen en krachten mogelijk maken. De radicale is de manier om wiskundig te symboliseren tot het n-beme van een bedrag "a". Deze wortel is een ander bedrag, "B" genoemd, zodat de naam precies "A" is, dus het is geldig om het volgende te schrijven:

De waarde van "n" is een natuurlijk getal, dat bekend staat als de root -index, "a" is de Radicerend of subradicale hoeveelheid, en "B" is het n -em van "a" wortel. Zowel "A" als "B" behoren tot de reeks reële getallen.

Als de index niet in een radicaal is geschreven, wordt onmiddellijk begrepen dat de waarde ervan gelijk is aan 2 en leest "vierkantswortel van A".

Aangezien "N" tot de reeks natuurlijke nummers behoort, kan dit een paar of oneven nummer zijn. Vervolgens worden de volgende gevallen onderscheiden:

Voor "n" par

• Als a> 0 of gelijk aan 0, is de n-alkale wortel van "a" positief of 0, en wordt aangeroepen hoofdwortel.
• Wanneer < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Voor "n" oneven

• Ja a> 0, het n -em van "a" root is positief.
• Wanneer< 0, la raíz n-ésima de “a” es negativa.

Enkele voorbeelden zijn de volgende:

Het filmen van eigenschappen

Het is mogelijk om de naam van een hoeveelheid van een bedrag te schrijven als een vermogen met fractionele exponent, dat wil zeggen een rationeel nummer.

In dit geval wordt de root -index de noemer, terwijl de exponent van de subradische hoeveelheid de teller wordt:

Kan u van dienst zijn: homografische functie: hoe u kunt grafieken, opgeloste oefeningen

Expressie die geldig is zolang n ≠ 0, omdat er geen breuken met een noemer worden toegelaten.

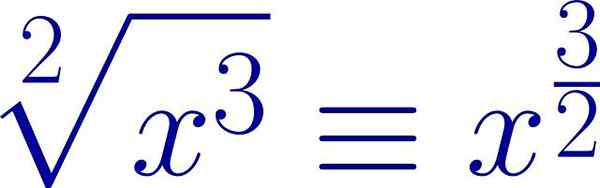Voorbeeld van een radicale uitdrukking geschreven in de vorm van een fractionele exponent. De root -index is de noemer van de exponent, terwijl de kracht van de uitzending de teller is. Bron: Wikimedia Commons.

Op deze manier kunnen dezelfde eigenschappen die van toepassing zijn op de bevoegdheden, worden gebruikt in het geval van radicalen.

Voor waarden die behoren tot de reeks reële getallen, zijn deze eigenschappen als volgt:

1. Radicaal product van gelijke index

In het product van twee (of meer) radicalen van dezelfde index worden de subradische hoeveelheden vermenigvuldigd, waardoor de index wordt gehandhaafd:

2. Radicaal quotiënt van dezelfde index

Het quotiënt tussen de n-die wortel van "a" en het n -em van "b", zijnde b ≠ 0, is gelijk aan de n-emeasy wortel van het quotiënt tussen "a" en "b":

3. Wortelwortel

Om de n-emasy-wortel van het m -em van de hoeveelheid "a" te vinden, is de subradische hoeveelheid geschreven onder een wortel waarvan de index het product is tussen "n" en "m":

De procedure is gemakkelijk uitgebreid tot opeenvolgende geneste wortels. De resulterende root -index is het product van alle indices, zoals deze:

4. Wortelkracht

Een N-dat, verhoogd tot de macht M, drukt het subradische bedrag uit voor de genoemde macht:

Bepaalde gevallen:

1) Ja n = m, Het wortelteken verdwijnt, waardoor de basis tot kracht 1 wordt verhoogd 1:

Die geldig is voor ≥ 0. Over het algemeen, als de root -index een even nummer is, heb je:

(Zie voorbeelden later)

2) Ja m> n, De M/N -fractie is ongepast en de wortel kan bijvoorbeeld worden vereenvoudig Eigenschappen die hier worden beschreven.

Kan u van dienst zijn: prisma's en piramides

(Zie voorbeelden later)

5. Radicale versterking

Een radicaal kan worden versterkt door een factor Q, Als zowel de root -index als de kracht van de subradische hoeveelheid, vermenigvuldigt u zich met genoemde factor, en deze bewerking houdt niet de wijziging van het resultaat in. Daarom:

Op voorwaarde dat een ≥ 0 wanneer het zelfs is.

6. Introductie van een factor binnen een radicaal

Als een positieve "B" -factor een radicaal vermenigvuldigt, kan deze erin passeren, als deze naar dezelfde wortelindex stijgt. In dat geval:

7. Som en aftrekking van radicalen

De radicalen kunnen toevoegen en aftrekken, zolang ze dezelfde index zijn en dezelfde subradische hoeveelheid hebben.

Wanneer twee of meer radicaal van gelijke index en subradische hoeveelheid zijn, wordt gezegd dat ze dat zijn Vergelijkbare radicalen.

De volgende radicalen zijn bijvoorbeeld vergelijkbaar:

In plaats daarvan zijn deze radicalen niet vergelijkbaar, omdat ze niet dezelfde subradische hoeveelheid hebben:

Noch zijn deze twee vergelijkbaar:

Omdat de radicale index niet hetzelfde is.

Soortgelijke radicalen kunnen worden gereduceerd tot één, het toevoegen of aftrekken van de bij hen vergezelde coëfficiënten.

Voorbeelden van radicale eigenschappen

voorbeeld 1

Wat is de waarde van de volgende wortels?

De vierkantswortel van 32 is direct te vinden met behulp van de rekenmachine. De waarde ervan is:

De suspensieve punten geven aan dat er oneindig decimaal is.

Als u liever niet met decimale getallen werkt, kan de vierkantswortel van 32 ook worden berekend door 32 te ontbinden in zijn belangrijkste factoren:

32 = 2⁵

Op deze manier wordt het bij vervanging verkregen:

Kan u van dienst zijn: divisors van 8: wat zijn en gemakkelijke uitleg

Geschreven als een fractionele exponent:

Fractie 5/2 is ongepast, dus de radicaal kan worden vereenvoudigd, met behulp van de eigenschappen van de bevoegdheden:

Nu de eigenschap 1 hierboven toepassen:

Daarom:

Voor zijn deel:

Sinds (−2)³ = −8.

Volgens eigenschap 4:

En ten slotte bestaat de vierkantswortel van −8 niet in de reeks reële getallen, hoewel in de complexe getallen.

Voorbeeld 2

Gegeven de volgende bewerking:

Is het mogelijk om het resultaat te verminderen?

Op voorwaarde dat de radicalen vergelijkbaar zijn, is het mogelijk om ze te verminderen, maar hiervoor moeten ze dezelfde index hebben en dezelfde subradische hoeveelheid. In het vorige voorbeeld werd gezien dat:

Een analoge procedure kan worden gebruikt om het eerste toevoegen te schrijven, zodat de subradische hoeveelheid gelijk is aan 2:

Deze radicaal is vergelijkbaar met de vorige. Wat betreft de vierkantswortel van 81, dit is daarom 9:

Voorbeeld 3

Welke eigenschappen is nodig om aan te solliciteren om deze bewerking uit te voeren?

We moeten eigenschappen 3 en 5 toepassen, die respectievelijk de wortel van een wortel en introductie van een radicale waarde zijn. Ten eerste is Property 5 van toepassing, om de "X" te introduceren die buiten de binnenste wortel valt:

En nu is de uitdrukking klaar om eigenschap 3 toe te passen en de respectieve indices van elke radicaal te vermenigvuldigen:

Referenties

1. Gonzales, D. 2011. Basicalgebra: theorie en praktijk. 2e. Editie.
2. Haeussler, E. 2012. Voorzetting. 1e. Editie. Pearson.
3. Khan Acadaem. Exponenten en radicalen. Hersteld van: Khanacademy.borg.
4. Larson, r. 2012. Voorzetting. 8e. Editie. Cengage leren.
5. Stewart, J. 2007. Wiskunde voor berekening. 5e. Editie. Cengage leren.