Lineair programmeren Waar is het voor, modellen, beperkingen, toepassingen

De lineair programmeren Het is een wiskundige methode die dient om een ​​functie te optimaliseren (maximaliseren of minimaliseren) een functie waarvan de variabelen onderhevig zijn aan beperkingen, zolang de functie en beperkingen lineair afhankelijk zijn van de variabelen.

Over het algemeen de functie om een ​​praktische situatie te optimaliseren, zoals de winst van een fabrikant waarvan de input, arbeid of machines beperkt zijn.

Figuur 1. Lineaire programmering wordt veel gebruikt om de winst te optimaliseren. Bron: PiqSels.

Een van de eenvoudigste gevallen is die van een lineaire functie om te maximaliseren, die alleen afhankelijk is van twee variabelen, genoemd Beslissingsvariabelen. Het kan vorm zijn:

Z = k₁X + K₂En

Met k₁ en k₂ constanten. Deze functie staat bekend als de Objectieve functie. Natuurlijk zijn er situaties die meer dan twee variabelen verdienen voor hun studie, die complexer zijn:

Z = k₁X₁ + k₂X₂ + k₃X₃ +.. .

En beperkingen worden ook wiskundig gemodelleerd door een systeem van vergelijkingen of ongelijken, even lineair in X En En.

De set oplossingen van dit systeem wordt genoemd Haalbare oplossingen of Haalbare punten. En onder de haalbare punten is er minstens één, die de objectieve functie optimaliseert.

Lineaire programmering werd onafhankelijk ontwikkeld door de Amerikaanse fysicus en wiskundige.

De probleemoplossende methode bekend als Simplex -methode Het is de oprichting van Dantzig, die werkte voor de US Air Force, de University of Berkeley en Stanford University.

Figuur 2. De wiskundigen George Dantzig (links) en Leonid Kantorovich (rechts). Bron: f. Zapata.

[TOC]

Lineaire programmeermodellen

De benodigde elementen om een ​​lineair programmeermodel op te zetten, geschikt voor een praktische situatie, zijn:

-Objectieve functie

-Beslissingsvariabelen

-Beperkingen

In de objectieve functie is wat u wilt bereiken gedefinieerd. Stel bijvoorbeeld dat het gewenst is om de winst te maximaliseren die zijn verkregen door de vervaardiging van bepaalde producten. Vervolgens wordt de "winst" -functie vastgesteld, volgens de prijs waartegen de producten worden verkocht.

In wiskundige termen kan deze functie worden uitgekort met summatie:

Z = ∑k_Je X_Je

In deze vergelijking, k_Je Het zijn coëfficiënten en x_Je zijn de beslissingsvariabelen.

Beslissingsvariabelen zijn de elementen van het systeem waarvan de controle is en hun waarden zijn positieve reële getallen. In het voorgestelde voorbeeld zijn de beslissingsvariabelen het bedrag van elk te vervaardigen product om de maximale versterking te verkrijgen.

Ten slotte hebben we de beperkingen, die lineaire vergelijkingen of ongelijkheden zijn in termen van de beslissingsvariabelen. Ze beschrijven de beperkingen aan het probleem, die bekend zijn en kunnen bijvoorbeeld de hoeveelheden grondstof die beschikbaar zijn in de productie zijn.

Kan u van dienst zijn: functies van hoger dan twee (voorbeelden)

Soorten beperkingen

U kunt een bedrag m beperkingen hebben, beginnend bij J = 1 tot J = m. Wiskundig zijn de beperkingen van drie soorten:

1. NAAR_J = ∑ a_IJ . X_Je
2. B_J ≥ ∑ b_IJ . X_Je
3. C_J ≤ ∑ c_IJ . X_Je

De eerste beperking is van het lineaire vergelijkingstype en betekent dat de waarde is_J, die bekend is, moet worden gerespecteerd.

De resterende twee beperkingen zijn lineaire ongelijkheden en betekent dat de B -waarden_J en C_J, bekend, kan worden gerespecteerd of overwonnen, wanneer het symbool dat verschijnt ≥ (groter of gelijk aan) of respect of niet overwonnen is, als het symbool ≤ is (minder dan of gelijk aan).

Modelvoorbeeld

De toepassingsgebieden zijn zeer divers en dekken van bedrijfskunde tot voeding, maar om de methode te begrijpen, wordt vervolgens een eenvoudig model van een praktische situatie met twee variabelen voorgesteld.

Een lokaal gebak staat bekend om twee specialiteiten: de Black Jungle Cake and the Sacrista Cake.

In zijn uitwerking vereisen ze eieren en suiker. Voor de zwarte jungle zijn er 9 eieren en 500 g suiker nodig, terwijl 8 eieren en 800 g suiker nodig zijn voor de sacripenine. De respectieve verkoopprijzen zijn $ 8 en 10.

Het probleem is: hoeveel taarten van elk type moeten het deeg moeten maken om de winst te maximaliseren, wetende dat het 10 kilo suiker en 144 eieren heeft?

Beslissingsvariabelen

De beslissingsvariabelen zijn "X" en "Y", die echte waarden nemen:

-X: De hoeveelheid zwarte jungle cakes

-Y: Sacriphantijnse type cakes.

Beperkingen

De beperkingen worden gegeven door het feit dat het aantal taarten een positieve hoeveelheid is en er beperkte hoeveelheden grondstof zijn om ze voor te bereiden.

Daarom verwerven deze beperkingen op de wiskundige manier de vorm:

1. x ≥ 0
2. en ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 en ≤ 10

Beperkingen 1 en 2 vormen de Niet -negativiteitstoestand Eerder blootgesteld, en alle verhoogde ongelijken zijn lineair. In beperkingen 3 en 4 zijn de waarden die niet moeten worden overwonnen: 144 eieren en 10 kg suiker.

Objectieve functie

Ten slotte is de objectieve functie de winst verkregen door de productie van "x" hoeveelheid zwarte jungle cakes plus "y" -hoeveelheid sacristines te produceren. Het is gebouwd vermenigvuldigingsprijs door de hoeveelheid gemaakte taarten en toevoeging voor elk type. Het is een lineaire functie die we g (x, y) zullen noemen:

G = 8x + 10y

Oplossingsmethoden

Een van de verschillende oplossingsmethoden zijn grafische methoden, het simplex -algoritme en de interne puntmethode, om enkele te noemen.

- Grafische of geometrische methode

Wanneer u een probleem heeft met twee variabelen zoals de vorige sectie, bepalen de beperkingen een polygonaal gebied in het vlak XY, telefoongesprek Haalbaar gebied of Levensvatbaarheidsgebied.

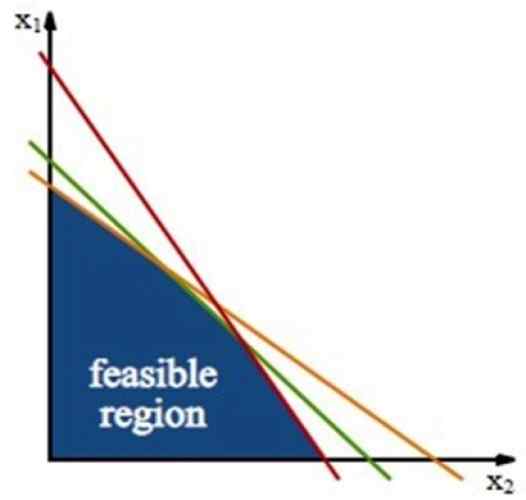figuur 3. Het haalbare gebied, waar de oplossing van het optimalisatieprobleem zich bevindt. Bron: Wikimedia Commons.

Deze regio is doorgebouwd door Beperkingslijnen, die de lijnen zijn die zijn verkregen uit de vermenigingen van de beperkingen, die alleen werken met het teken van gelijkheid.

Kan u van dienst zijn: eindige set: eigenschappen, voorbeelden, opgeloste oefeningen

In het geval van bakkerij die de winst wil optimaliseren, zijn beperkingslijnen:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Alle punten in de regio die door deze lijnen worden vergrendeld, zijn mogelijke oplossingen, dus er zijn oneindig. Behalve in het geval waarin de haalbare regio leeg is, mist het probleem dat op de hoogte wordt gebracht een oplossing.

Gelukkig is de haalbare regio voor het deegprobleem niet leeg, we hebben het hieronder.

Figuur 4. Het haalbare gebied van het gebaksprobleem. De rechte lijn 0 kruist de oorsprong. Bron: f. Zapata met Geogebra.

De optimale oplossing, als deze bestaat, is met behulp van de objectieve functie. Als het gaat om het vinden van de maximale G -versterking, hebt u bijvoorbeeld de volgende regel, die wordt genoemd ISO-BENEFICE recht:

G = k₁X + K₂en → y = -k₁X / K₂ + G/ K₂

Met deze lijn worden alle paren (x, y) verkregen die een gegeven winst G bieden, dus er is een familie van lijnen volgens de waarde van G, maar allemaal met dezelfde helling -k₁ / K₂, Zodat ze parallel recht zijn.

De optimale oplossing

Nu kan worden aangetoond dat de optimale oplossing van een lineair probleem altijd een extreme of hoekpunt van het haalbare gebied is. Dus:

De lijnoplossing is het verst van de oorsprong en dat heeft ten minste één punt gemeen met het haalbare gebied.

Als de lijn die het dichtst bij de oorsprong ligt een heel segment gemeen heeft met de haalbare regio, wordt gezegd dat er oneindige oplossingen zijn. Deze case treedt op als de helling van de ISO-Benefits-lijn gelijk is aan die van een van de andere lijnen die de regio beperken.

Voor ons gebak zijn de kandidaat -hoekpunten A, B en C.

- Simplex -methode van Dantzig

De grafische of geometrische methode is van toepassing op twee variabelen. Het is echter ingewikkelder als er drie variabelen zijn en onmogelijk te gebruiken voor een groter aantal variabelen.

Als het gaat om problemen van meer dan twee variabelen, de Simplex -methode, die bestaat uit een reeks algoritmen om objectieve functies te optimaliseren. Eenvoudige matrices en rekenkunde worden meestal gebruikt om de berekeningen uit te voeren.

De simplex -methode begint door een haalbare oplossing te kiezen en te controleren of deze optimaal is. Als het is, hebben we het probleem al opgelost, maar als dat niet het geval is, gaat het door naar een oplossing die dichter bij optimalisatie is. Als de oplossing bestaat, is het algoritme erbij in een paar pogingen.

Kan u van dienst zijn: wat is de statistiekenbereik? (Met voorbeelden)

Toepassingen

Lineaire en niet-lineaire programmering die op veel gebieden wordt toegepast om de beste beslissingen te nemen bij het verlagen van de kosten en het verhogen van de winst, die niet altijd monetair zijn, omdat ze op tijd kunnen worden gemeten, bijvoorbeeld als u de benodigde tijd wilt minimaliseren om uit te voeren Een reeks operaties.

Hier zijn enkele velden:

-In marketing wordt het gebruikt om de beste combinatie van media (sociale netwerken, televisie, pers en anderen) te vinden om een ​​bepaald product te adverteren.

-Voor de toewijzing van werk dat geschikt is voor het personeel van een bedrijf of fabriek of schema's voor hen.

-Bij de selectie van het meest voedzame voedsel en tegen de laagste kosten in vee- en pluimvee -industrie.

Opgeloste oefeningen

- Oefening 1

Grafiek het lineaire programmeermodel dat in de voorgaande secties is verhoogd.

Oplossing

Het is noodzakelijk om de set waarden te verwezenlijken die zijn bepaald door het systeem van beperkingen die in het probleem zijn gespecificeerd:

1. x ≥ 0
2. en ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 en ≤ 10

De regio gegeven door vermengingen 1 en 2 komt overeen met het eerste kwadrant van het Cartesiaanse vlak. Wat betreft ongelijken 3 en 4, het begint met het vinden van de restrictielijnen:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

De haalbare regio is een vierhoek waarvan de hoekpunten punten A, B, C en D zijn.

De minimale versterking is 0, daarom is de 8x + 10 en 10 -lijn de ondergrens en de ISO -batenlijnen hebben in afwachting van -8/10 = -0.8.

Deze waarde verschilt van de hellingen van de andere restrictielijnen en omdat het haalbare gebied beperkt is, is er de unieke oplossing.

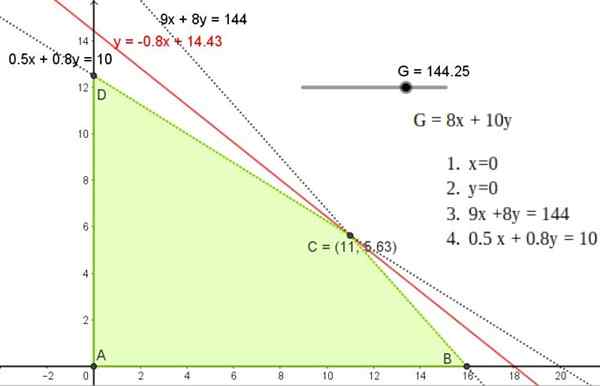Figuur 5. Grafische oplossing van oefening 1, met het haalbare gebied en de puntoplossing C in een van de hoekpunten van het genoemde gebied. Bron: f. Zapata.

Deze oplossing komt overeen met een hellingslijn -0.8 die door een van de punten A, B of C gaat, wiens coördinaten zijn:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Optimale oplossing

We berekenen de waarde van G voor elk van deze punten:

-(11; 5.625): g_NAAR = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): g_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): G_C = 8 x 16 + 10 x 0 = 128

De grootste winst is het produceren van 11 zwarte jungle cakes en 5.625 Sacripantijne taarten. Deze oplossing is het eens met degene die via de software wordt gevonden.

- Oefening 2

Controleer het resultaat van de vorige oefening met behulp van de functie Solver (Solutioner) die beschikbaar is in de meeste spreadsheets zoals Excel of Calc de LibreOffice, die het simplex -algoritme bevatten voor lineaire programmeeroptimalisatie.

Oplossing

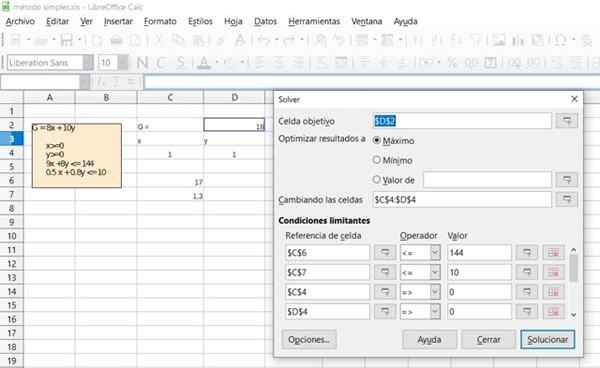Figuur 6. Detail van de oplossing van Oefening 1 via de Free Office Calc -spreadsheet. Bron: f. Zapata. 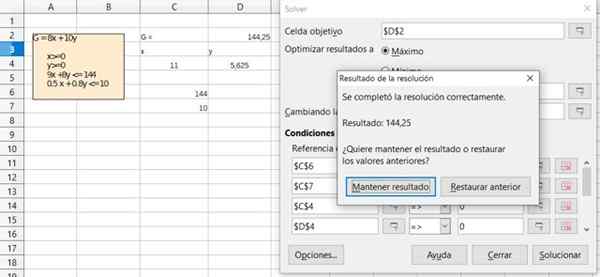Figuur 7. Detail van de oplossing van Oefening 1 via de Free Office Calc -spreadsheet. Bron: f. Zapata.

Referenties

1. Briljant. Lineair programmeren. Hersteld van: briljant.borg.
2. Eppen, g. 20000000000000000000. Operations Research in Administrative Science. 5e. Editie. Prentice Hall.
3. Haeussler, E. 1992. Wiskunde voor administratie en economie. 2e. Editie. Ibero -Amerikaanse redactionele groep.
4. Hiru.EUS. Lineair programmeren. Hersteld van: Hiru.EUS.
5. Wikipedia. Lineair programmeren. Hersteld van: is. Wikipedia.borg.