Dynamische programmeerkenmerken, bijvoorbeeld voor-, nadelen

De Dynamisch programmeren Het is een algoritmemodel dat een complex probleem oplost door het in subproblemen te delen, hun resultaten op te slaan om te voorkomen dat ze die resultaten moeten berekenen.

Dit programma wordt gebruikt wanneer problemen kunnen worden onderverdeeld in vergelijkbare subproblemen, zodat hun resultaten kunnen worden hergebruikt. Voor de meeste meerderheid wordt dit programma gebruikt voor optimalisatie.

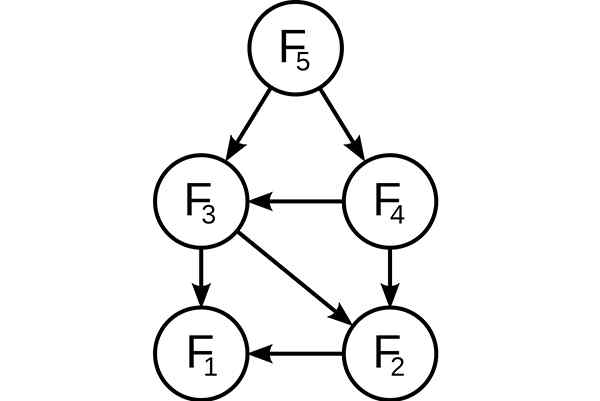
Dynamisch programmeren. Subproblems bovenop in de opvolging van de Fibonacci. Bron: Wikimedia Commons, AT: Gebruiker: Dcoatzee, getraceerd door gebruiker: Stannered / Public Domain

Voordat het beschikbare subprobleem wordt opgelost, zal het dynamische algoritme proberen de resultaten van de eerder opgeloste subproblemen te onderzoeken. Subproblems -oplossingen worden gecombineerd om de beste oplossing te bereiken.

In plaats van dezelfde subproblema steeds opnieuw te berekenen, kan uw oplossing in een bepaald geheugen worden opgeslagen, wanneer u voor het eerst deze subproblema ontmoet. Wanneer het opnieuw verschijnt tijdens de oplossing van een ander subprobleem, wordt de oplossing die al in het geheugen is opgeslagen, worden genomen.

Dit is een geweldig idee om de tijd met geheugen te corrigeren, waar u bij het gebruik van extra ruimte de tijd kunt verbeteren die nodig is om een ​​oplossing te vinden.

[TOC]

Kenmerken van dynamisch programmeren

De volgende essentiële kenmerken zijn die welke een probleem kan worden toegepast voor dynamische programmering:

Optimale substructuur

Dit kenmerk geeft aan dat een optimalisatieprobleem kan worden opgelost door de optimale oplossingen van de secundaire problemen die het vormen te combineren. Deze optimale substructuren worden beschreven door recursie.

In een grafiek wordt bijvoorbeeld een optimale substructuur gepresenteerd op de kortste route die van een hoekpunt naar een hoekpunt gaat:

Dat wil zeggen, op deze kortste route r kunt u elk tussenliggende hoekpunt I nemen. Als R echt de kortste route is, kan deze worden verdeeld in de subrutas R1 (van S tot I) en R2 (van i tot t), zodat deze op hun beurt de kortste routes zijn tussen de overeenkomstige hoekpunten.

Daarom kunt u, om de kortste routes te vinden, de oplossing gemakkelijk recursief formuleren, wat het Floyd-Warshall-algoritme doet.

SUPPERPOSEN SUBPROBLEMEN

De ruimte van de subproblemen moet klein zijn. Dat wil zeggen, elk recursief algoritme dat een probleem oplost, moet steeds opnieuw dezelfde subproblemen oplossen, in plaats van nieuwe subproblemen te genereren.

Om bijvoorbeeld de Fibonacci-serie te genereren, kan deze recursieve formulering worden overwogen: fn = f (n-1) + f (n-2), waarbij een basisgeval wordt gebruikt dat f1 = f2 = 1. Dan moet je: F33 = F32 + F31 en F32 = F31 + F30.

Zoals te zien is, wordt F31 opgelost in de recursieve sub -seasons van zowel F33 als F32. Hoewel het totale aantal subproblemen echt klein is, als een recursieve oplossing wordt aangenomen, omdat dit steeds opnieuw dezelfde problemen zal oplossen.

Kan u van dienst zijn: de 7 componenten van een informatiesysteem

Hiermee wordt rekening gehouden door dynamische programmering, dus het lost elk subprobleem slechts eenmaal op. Dit kan op twee manieren worden bereikt:

Topbenadering

Als de oplossing voor elk probleem recursief kan worden geformuleerd met behulp van de oplossing van hun subproblemen, en als deze subproblemen overlappen, kunnen de oplossingen voor de subproblemen eenvoudig worden onthouden of opgeslagen in een tabel in een tabel.

Elke keer dat de oplossing van een nieuwe subproblema wordt gevraagd, wordt deze in de tabel beoordeeld als het eerder is opgelost. In het geval dat een oplossing wordt opgeslagen, wordt deze gebruikt in plaats van deze opnieuw te berekenen. Anders wordt de subproblema opgelost, waarbij de oplossing in de tabel wordt opgeslagen.

Stijgende aanpak

Nadat de oplossing van een probleem recursief is geformuleerd in termen van zijn subproblems, kan het probleem in een opwaartse worden geprobeerd: eerst zullen ze proberen de subproblemen op te lossen en hun oplossingen te gebruiken om oplossingen te bereiken voor de grootste subproblemen.

Dit wordt meestal ook gedaan in de vorm van een tabel, waardoor iteratieve oplossingen worden gegenereerd voor steeds grotere subproblemen door oplossingen te gebruiken voor kleine subproblemen. Als de waarden van F31 en F30 bijvoorbeeld al bekend zijn, kan de waarde van F32 direct worden berekend.

Vergelijking met andere technieken

Een aanzienlijk behoren tot een probleem dat kan worden opgelost door dynamische programmering is dat het overlappende subproblemen zou moeten hebben. Dit onderscheidt de dynamische programmering van de techniek van het delen en veroveren, waar het niet nodig is om de eenvoudigste waarden op te slaan.

Het is vergelijkbaar met recursie, omdat door het berekenen van basisgevallen de uiteindelijke waarde inductief kan worden bepaald. Deze stijgende aanpak werkt goed wanneer een nieuwe waarde alleen afhangt van eerder berekende waarden.

Voorbeeld

Minimale stappen om 1 te bereiken

Voor elk positief gehele nummer "E" kunt u een van de volgende drie stappen uitvoeren.

- Trek 1 af van het nummer. (E = E-1).

- Als het deelbaar is door 2, wordt het gedeeld door 2 (als E%2 == 0, dan E = E/2).

- Als het deelbaar is door 3, wordt het gedeeld door 3 (als E%3 == 0, dan E = E/3).

Op basis van de vorige stappen moet u het minimale bedrag van deze stappen vinden en 1. Bijvoorbeeld:

- Als e = 1, resultaat: 0.

- Als e = 4, resultaat: 2 (4/2 = 2/2 = 1).

- Wanneer e = 7, resultaat: 3 (7-1 = 6/3 = 2/2 = 1).

Benadering

Misschien denk je altijd aan het kiezen van de stap die n zo laag mogelijk maakt en zo doorgaat, totdat deze 1 bereikt. Het is echter te zien dat deze strategie hier niet werkt.

Kan u van dienst zijn: commerciële software

Als bijvoorbeeld E = 10, zouden de stappen zijn: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 stappen). De optimale manier is echter: 10-1 = 9/3 = 3/3 = 1 (3 stappen). Daarom moeten alle mogelijke stappen die voor elke waarde van n worden gebracht, worden bewezen, waardoor het minimale bedrag van deze mogelijkheden wordt gekozen.

Het begint allemaal met recursie: f (e) = 1 + min f (e-1), f (e/2), f (e/3) als e> 1, als basiscase: f (1 ) = 0. Met de herhalingsvergelijking kunt u beginnen met het coderen van de recursie.

Er kan echter worden opgemerkt dat het opgevumpt subproblemen heeft. Bovendien hangt de optimale oplossing voor een gegeven input af van de optimale oplossing van zijn subprobleem.

Zoals in het onthouden, waar de oplossingen van de opgeloste subproblemen worden opgeslagen om ze later te gebruiken. Of zoals in dynamische programmering, begint het van onderaf, door te gaan naar de gegeven E. Vervolgens beide codes:

Memorisatie

Dynamische opwaartse programmering

Voordelen

Een van de belangrijkste voordelen van het gebruik van dynamische programmering is dat het de verwerking versnelt, aangezien eerder berekende referenties worden gebruikt. Net als een recursieve programmeertechniek, vermindert het programmacoderegels.

Vorace Algoritmos versus dynamisch programmeren

Voorkastige algoritmen zijn vergelijkbaar met dynamische programmering in de zin dat beide hulpmiddelen zijn voor optimalisatie. Het Voraz -algoritme zoekt echter een optimale oplossing in elke lokale stap. Dat wil zeggen, het zoekt een hebzuchtige keuze in de hoop een wereldwijde optimale te vinden.

Daarom kunnen vraatzuchtige algoritmen een veronderstelling maken die er op dat moment optimaal uitziet, maar dat wordt in de toekomst duur en garandeert.

Aan de andere kant vindt dynamische programmering de optimale oplossing voor subproblemen en maakt vervolgens een weloverwogen keuze door de resultaten van die subproblemen te combineren om echt de meest optimale oplossing te vinden.

Nadelen

- Veel geheugen is nodig om het berekende resultaat van elk subprobleem op te slaan, zonder ervoor te zorgen dat de opgeslagen waarde zal worden gebruikt of niet.

- Vaak wordt de uitgangswaarde opgeslagen zonder ooit te worden gebruikt in de volgende subproblemen tijdens de uitvoering. Dit leidt tot onnodig gebruik van geheugen.

- In dynamische programmering worden de functies recursief genoemd. Hierdoor blijft het batterijgeheugen constant toenemen.

Recursiviteit versus dynamisch programmeren

Als u een beperkt geheugen heeft om de code uit te voeren en de verwerkingssnelheid niet zorgwekkend is, kan recursiviteit worden gebruikt. Als een mobiele applicatie bijvoorbeeld wordt ontwikkeld, is het geheugen zeer beperkt om de applicatie uit te voeren.

Kan u van dienst zijn: gemengde apparaten: kenmerken en voorbeelden

Als het programma gewenst is om sneller te worden uitgevoerd en er geen geheugenbeperkingen zijn, heeft het de voorkeur om dynamisch programmeren te gebruiken.

Toepassingen

Dynamische programmering is een effectieve methode om problemen op te lossen die anders in een redelijke tijd extreem moeilijk lijken te lijken.

Algoritmen op basis van het dynamische programmeerparadigma worden gebruikt in veel wetenschapsgebieden, waaronder veel voorbeelden in kunstmatige intelligentie, van de oplossing van planningsproblemen tot stemherkenning.

Dynamische programmeeralgoritmen

Dynamische programmering is vrij effectief en dient zeer goed voor een breed scala aan problemen. Veel algoritmen kunnen worden gezien als toepassingen van vraatzuchtige algoritmen, zoals:

- Fibonacci -nummers serie.

- Hanoi -torens.

- Alle kortste routes paren van Floyd-Warshall.

- Rugzak.

- Projectprogrammering.

- Het kortste pad door Dijkstra.

- Robotics Flight Control and Control.

- Wiskundige optimalisatieproblemen.

- Gedeelde tijd: programmeer het werk om het gebruik van de CPU te maximaliseren.

Fibonacci -nummers serie

Fibonacci -getallen zijn de getallen die in de volgende volgorde worden gevonden: 0, 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144, enz.

In wiskundige terminologie wordt de FN -opvolging van Fibonacci -getallen gedefinieerd door de recidiefformule: F (n) = f (n -1) + f (n -2), waarbij f (0) = 0 en f (1) = 1.

Topbenadering

In dit voorbeeld wordt een zoekmatrix met alle beginwaarden geïnitialiseerd met -1. Wanneer de oplossing voor een subprobleem nodig is, zal deze eerst worden gezocht in deze zoekmatrix.

Als er de berekende waarde is, wordt die waarde geretourneerd. Anders wordt het resultaat berekend om het in de zoekmatrix op te slaan en dus in staat te zijn om het later opnieuw te gebruiken.

Stijgende aanpak

In dit geval wordt voor dezelfde Fibonacci -serie F (0), vervolgens F (1), F (2), F (3), enzovoort, eerst berekend. Zo zullen de oplossingen van de subprobleem van de onderkant worden gebouwd.

Referenties

1. Vineet Choudhary (2020). Inleiding tot dynamisch programmeren. Unbevelder Insider.Uitgevoerd uit: Developerinsider.co.
2. Alex Allain (2020). Dynamische programmering in C++. C -programmering. Uitgehaald uit: cprogrammmming.com.
3. After Academy (2020). Idee van dynamisch programmeren. Uitgevoerd uit: Afteracademy.com.
4. Aniruddha Chaudhari (2019). Dynamische programmering en recursie | Verschillend. CSE -stapel. Genomen uit: csestack.borg.
5. Code Chef (2020). Voor dynamische programmeeropleiding. Genomen van: codhef.com.
6. Programiz (2020). Dynamisch programmeren. Genomen uit: Programiz.com.