Politropische proceskenmerken, toepassingen en voorbeelden

A Politropisch proces Het is een thermodynamisch proces dat optreedt wanneer de relatie tussen druk P en het volume V gegeven door P.V^N Het blijft constant. De exponent N Het is een reëel getal, meestal tussen nul en oneindig, maar dat kan in sommige gevallen negatief zijn.

De waarde van N Ontvang de naam van Politropische index En het is belangrijk om te benadrukken dat tijdens een polytropisch thermodynamisch proces dat de index een vaste waarde moet behouden, anders wordt het proces niet als polytropisch beschouwd.

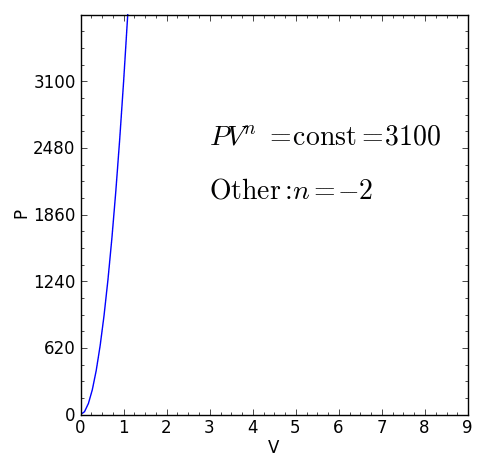
Figuur 1. Karakteristieke vergelijking van een polytropisch thermodynamisch proces. Bron: f. Zapata.

[TOC]

Kenmerken van polytropische processen

Sommige karakteristieke gevallen van polytropische processen zijn: 

- Het isothermische proces (bij constante t -temperatuur), waarbij de exponent n = 1 is.

- Een isobarisch proces (constante druk p), in dit geval n = 0.

- Het isocorische proces (tot volume V -constante), waarvoor n =+∞.

- Adiabatische processen (tot constante entropie), waarbij de exponent n = γ is, is γ de adiabatische constante. Deze constante is het quotiënt tussen de warmtecapaciteit bij constante druk CP gedeeld door de warmtecapaciteit bij constant CV -volume:

γ = CP/CV

- Elk ander thermodynamisch proces dat geen van de vorige gevallen is. Maar voldoet P.V^N = CTTE Met echte en constante polytropische index N Het zal ook een polytropisch proces zijn.

Figuur 2. Verschillende karakteristieke gevallen van polytropische thermodynamische processen. Bron: Wikimedia Commons.

Toepassingen

Een van de belangrijkste toepassingen van de polytropische vergelijking is voor de berekening van het werk dat wordt uitgevoerd door een gesloten thermodynamisch systeem, wanneer het op een quasi -statische manier van een initiële toestand naar een ander uiteinde gaat, dat wil zeggen, dat wil zeggen een opeenvolging van evenwichtstoestanden na.

Werk in polytropische processen voor verschillende waarden van n

Voor n ≠ 1

Mechanisch werk dat wordt uitgevoerd door een gesloten thermodynamisch systeem wordt berekend door expressie:

W = ∫p.Dv

Kan u van dienst zijn: diamagnetisme: materialen, toepassingen, voorbeelden

Waarbij p de druk is en v het volume.

Zoals in het geval van een polytropisch proces is de relatie tussen druk en volume:

P.V ^N = constant = c

Het wissen van P van de vorige uitdrukking om deze te vervangen in de uitdrukking van werk:

P = c /V ^N

U hebt het mechanische werk gedaan tijdens een polytropisch proces, dat begint in een initiële toestand 1 en eindigt in de laatste toestand 2. Dit alles verschijnt in de volgende uitdrukking:

Als n ≠ 1, dan heb je:

Bovendien, aangezien de initiële en uiteindelijke toestanden goed zijn gedefinieerd, wordt de constante ook bepaald door de volgende uitdrukking:

C = P₁ V₁^N = P₂ V₂^N

Door de waarde van de constante in de expressie van werk te vervangen, wordt verkregen:

W = (p₂ V₂ - P₁ V₁)/(1-n)

In het geval dat de werkstof kan worden gemodelleerd als een ideaal gas, is de volgende staatsvergelijking:

P.V = m.R.T

Waarbij m het aantal mol ideaal gas is en R de universele constante van gassen is.

Voor een ideaal gas dat volgt op een polytropisch proces met een polytropie -index die verschilt van de eenheid en die van een toestand passeert met de initiële temperatuur T₁ naar een andere toestand met temperatuur T₂ Het werk wordt gegeven door de volgende formule:

W = m r (t₂ - T₁)/(1-n)

Voor n → ∞

Volgens de formule voor het werk dat in de vorige sectie is verkregen, is het werk van een polytropisch proces met n = ∞ nul, omdat de expressie van werk is verdeeld tussen oneindig en daarom is het resultaat de neiging tot nul.

Een andere manier om dit resultaat te bereiken is om te beginnen met de P -relatie₁ V₁^N = P₂ V₂^N, die als volgt kan worden herschreven:

(P₁/P₂) = (V₂/V1)^N

N-dikker root nemen in elk lid dat u krijgt:

(V₂/V1) = (p₁/P₂))^(1/n)

In het geval dat n → ∞ moet je (v₂/V1) = 1, wat betekent dat:

Kan u van dienst zijn: afgestudeerde hitte: formules, hoe u het kunt berekenen en oefeningen opgelost

V₂ = V₁

Dat wil zeggen, het volume verandert niet in een polytropisch proces met n → ∞. Daarom is het dv -volumeverschillen in de integrale van mechanisch werk 0. Dit soort polytropische processen staan ​​ook bekend als processen isocorisch, o Processen bij constant volume.

Voor n = 1

Nogmaals, we hebben de uitdrukking voor werk:

W = ∫p dv

In het geval van een polytropisch proces met n = 1 is de relatie tussen druk en volume:

P v = constant = c

Door P van de vorige uitdrukking en vervanging te wissen, hebt u het werk gedaan om van de initiële status 1 naar de laatste status 2 te gaan:

W = ∫12p dv = ctte ∫12 v^( - 1) dv = ctte (ln (v2) - ln (v1))

Het is te zeggen:

W = c ln (v₂/V₁)).

Aangezien de initiële en uiteindelijke toestanden goed zijn bepaald, zal de CTTE ook. Het is te zeggen:

C = P₁ V₁ = P₂ V₂

Ten slotte zijn de volgende nuttige uitdrukkingen beschikbaar om het mechanische werk te vinden van een polyitropisch gesloten systeem waarin n = 1.

W = p₁ V₁ ln (v₂/V₁) = P₂ V₂ ln (v₂/V₁))

Als de werkstof bestaat uit M Mol ideaal gas, dan kan de ideale gasvergelijking worden toegepast: P V = M.R.T.

In dit geval, zoals P.V₁ = CTTE, een polytropisch proces met n = 1 is een proces bij constante t -temperatuur (isotherme), zodat de volgende uitdrukkingen voor werk kunnen worden verkregen:

W = m r t₁ ln (v₂/V₁) = m r t₂ ln (v₂/V₁))

figuur 3. Een caramban smelten, voorbeeld van isotherme proces. Bron: Pixabay.

Voorbeelden van polytropische processen

- voorbeeld 1

Ga uit van een cilinder met een beweegbare zuiger vol met een kilogram lucht. Aanvankelijk bezet de lucht een volume V₁= 0,2 m³ bij een druk p₁= 400 kPa. Een polytropisch proces wordt gevolgd met n = γ = 1,4, waarvan de uiteindelijke toestand druk heeft₂ = 100 kPa. Bepaal het werk dat wordt gedaan door de lucht op de zuiger.

Oplossing

Wanneer de polytropie -index gelijk is aan de adiabatische constante, is er een proces waarbij de werkstoffen (lucht) geen warmte uitwisselt met de omgeving en daarom geen entropie verandert.

Het kan u van dienst zijn: Derde wet van thermodynamica: formules, vergelijkingen, voorbeelden

Voor lucht, een ideaal diatomisch gas, heb je:

γ = cp/cv, met cp = (7/2) r en cv = (5/2) r

Dus:

γ = 7/5 = 1.4

Met behulp van de expressie van het polytropische proces kan het uiteindelijke volume van de lucht worden bepaald:

V₂ = [P₂ V₁^1.4)/P₂]^(1/1.4) = 0,54 m³.

Nu zijn er voorwaarden om de werkformule in een polytropisch proces toe te passen voor n ≠ 1 hierboven verkregen:

W = (p₂ V₂ - P1 v1)/(1-n)

De juiste waarden vervangen zijn:

W = (100 kPa 0,54 m³ - 400 kPa 0,2 m³)/(1 - 1.4) = 65,4 kJ

- Voorbeeld 2

Ga uit van dezelfde cilinder van voorbeeld 1, met een beweegbare zuiger vol met een kilogram lucht. Aanvankelijk bezet de lucht een volume v1 = 0,2 m³ Bij een druk p1 = 400 kPa. Maar in tegenstelling tot het vorige geval breidt de lucht isotherme uit om een ​​uiteindelijke druk te bereiken P2 = 100 kPa. Bepaal het werk dat wordt gedaan door de lucht op de zuiger.

Oplossing

Zoals eerder gezien, zijn isothermische processen polytropische processen met index n = 1, dus wordt vervuld dat:

P1 V1 = P2 V2

Op deze manier kan het uiteindelijke volume gemakkelijk worden losgemaakt om te verkrijgen:

V2 = 0,8 m³

Vervolgens met de expressie van het eerder verkregen werk voor het geval n = 1 moet u door de lucht op de zuiger in dit proces werken:

W = p1 v1 ln (v2/v1) = 400000 pa × 0,2 m³ ln (0,8/0,2) = 110,9 kJ.  

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Cengel, en. 2012. Thermodynamica. 7e editie. McGraw Hill.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 4. Vloeistoffen en thermodynamica. Uitgegeven door Douglas Figueroa (USB).
4. López, c. De eerste wet van de thermodynamica. Hersteld van: culturracientifica.com.
5. Ridder, r. 2017. Fysica voor wetenschappers en engineering: een strategiebenadering. Pearson.
6. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9na ed. Cengage leren.
7. Sevilla University. Thermische machines. Hersteld van: laplace.ons.is.
8. Wikiwand. Politropisch proces. Hersteld van: Wikiwand.com.