Theoretische waarschijnlijkheid hoe het eruit te krijgen, voorbeelden, oefeningen

De Theoretische waarschijnlijkheid (of van laplace) dat er een gebeurtenis plaatsvindt die tot een steekproefruimte behoort, waarbij alle gebeurtenissen dezelfde kans hebben op voorkomen, wordt deze gedefinieerd in wiskundige notatie zoals: p (e) = n (e) / n ( S)

Waarbij p (e) de waarschijnlijkheid is, gegeven als de verhouding tussen het totale aantal mogelijke resultaten van de e -gebeurtenis, die we n (e) noemen, gedeeld door het totale aantal n (s) van mogelijke resultaten in de steekproefruimte s.

Figuur 1. Bij de lancering van een dobbelstenen met zes zegenen is de theoretische waarschijnlijkheid dat het gezicht met drie stippen bovenaan staat ⅙. Bron: Pixabay.

De theoretische waarschijnlijkheid is een reëel getal tussen 0 en 1, maar het wordt vaak uitgedrukt in de vorm van een percentage, in welk geval de waarschijnlijkheid een waarde tussen 0% en 100% zal zijn.

Het berekenen van de kans op het optreden van een evenement is op veel gebieden erg belangrijk, zoals aandelenmarktactiviteiten, verzekeringsmaatschappijen, gokken en nog veel meer.

[TOC]

Hoe u de theoretische waarschijnlijkheid kunt krijgen?

Een illustratief geval is het geval van rifas of loterijen. Neem aan dat 1.000 tickets voor Rifar een smartphone. Omdat de loterij willekeurig wordt gedaan, heeft elk van de tickets dezelfde kans om een ​​winnaar te zijn. 

Om de kans te vinden dat een persoon die een ticket koopt met nummer 81 winnaar is, de volgende berekening van Theoretische waarschijnlijkheid:

P (1) = 1/1.000 = 0,001 = 0,1%

Het vorige resultaat wordt als volgt geïnterpreteerd: als de loterij oneindig wordt herhaald, elke 1.000 keer ticket 81 zou gemiddeld eenmaal worden geselecteerd.

Als iemand om welke reden dan ook alle tickets verwerft, is er zeker van dat hij de prijs zal winnen. De kans om de prijs te winnen als je alle tickets als volgt hebt berekend:

Het kan u van dienst zijn: Perimeter van de cirkel: hoe u het eruit haalt en formules, opgeloste oefeningen

P (1.000) = 1.000/1.000 = 1 = 100%.

Dat wil zeggen, welke kans 1 of 100% betekent dat het volledig zeker is dat dit resultaat zal optreden.

Als iemand 500 tickets bezit, zijn de mogelijkheden om te winnen of te verliezen hetzelfde. De theoretische waarschijnlijkheid om de prijs in dit geval te winnen, wordt als volgt berekend:

P (500) = 500/1.000 = ½ = 0,5 = 50%.

Hij die geen ticket koopt, heeft geen kans om te winnen en zijn theoretische waarschijnlijkheid wordt als volgt bepaald:

 P (0) = 0/1.000 = 0 = 0%

Voorbeelden

voorbeeld 1

Je hebt een valuta mee duur aan de ene kant en schild of afdicht in de andere. Wanneer de valuta wordt gelanceerd, wat is de theoretische waarschijnlijkheid om duur te zijn?

P (duur) = n (duur) / N ( gezicht + schild ) = ½ = 0,5 = 50%

Het resultaat wordt als volgt geïnterpreteerd: als een groot aantal releases zou worden gemaakt, gemiddeld in elke 2 velden zou een van hen worden geconfronteerd.

In percentage termen is de interpretatie van het resultaat dat het maken van een oneindig groot aantal lanceringen gemiddeld elke 100 50 zou resulteren in duur.

Voorbeeld 2

In een doos zijn er 3 blauwe knikkers, 2 rode knikkers en 1 groen. Wat is de theoretische waarschijnlijkheid dat wanneer u een marmer uit de doos krijgt, dit rood is?

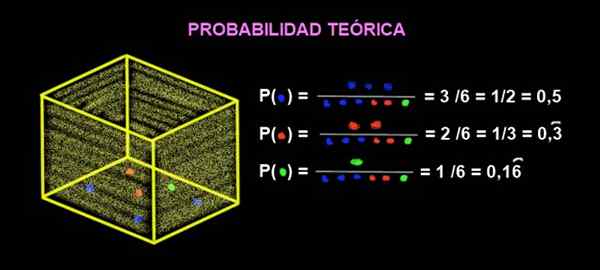Figuur 2. Waarschijnlijkheid van extractie van kleurmarmer. Bron: f. Zapata.

De waarschijnlijkheid die rood komt, is:

P (rood) = Aantal gunstige gevallen / aantal mogelijke gevallen

Het is te zeggen:

P (rood) = Aantal rode knikkers / totaal aantal knikkers

Ten slotte is de kans dat een rood marmer is:

P (rood) = 2/6 = ⅓ = 0.3333 = 33,33%

Terwijl de kans dat door een groen marmer te extraheren is:

P (groen) = ⅙ = 0,1666 = 16,66%

Ten slotte is de theoretische waarschijnlijkheid om in een blinde extractie een blauw marmer te verkrijgen: 

P (blauw) = 3/6 = ½ = 0,5 = 50%

Het kan u van dienst zijn: radicale eigenschappen

Dat wil zeggen, van elke 2 pogingen zal het resultaat blauw zijn in een van hen en een andere kleur in een andere poging, onder het uitgangspunt dat het geëxtraheerde marmer wordt aangevuld en dat het aantal proeven heel, heel groot is.

Opdrachten

Oefening 1

Bepaal de kans dat bij het starten van een dobbelstenen een waarde minder dan of gelijk is aan 4.

Oplossing

Om de kans te berekenen dat deze gebeurtenis plaatsvindt, is de definitie van theoretische waarschijnlijkheid van toepassing:

P (≤4) = Aantal gunstige gevallen / aantal mogelijke gevallen

P (≤5) = 5/6 = = 83,33%

Oefening 2

Zoek de kans dat in twee opeenvolgende toonhoogtes van een normale zeszijdige dobbelstenen, 2 keer 2 keer.

Oplossing

Om op deze oefening te reageren, is het handig om een ​​foto te maken om alle mogelijkheden te tonen. De eerste figuur geeft het resultaat aan van de eerste dobbelstenen en de tweede het resultaat van de andere.

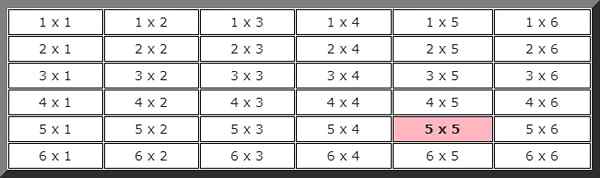
Om de theoretische waarschijnlijkheid te berekenen, moeten we het totale aantal mogelijke gevallen kennen, in dit geval zoals te zien in de vorige tabel, er zijn 36 mogelijkheden.

Ook het schilderij waarnemen hieruit volgt dat het aantal gevallen dat gunstig is voor het evenement dat in de twee opeenvolgende releases 5 slechts 1 is, gemarkeerd met kleur, daarom is de kans dat deze gebeurtenis zal gebeuren:

P (5 x 5) = 1/33.

Dit resultaat had ook kunnen worden bereikt met behulp van een van de eigenschappen van theoretische waarschijnlijkheid, die stelt dat de gecombineerde waarschijnlijkheid van twee onafhankelijke gebeurtenissen het product is van hun individuele waarschijnlijkheden.

In dit geval is de kans dat in de eerste release 5 ⅙ is. De tweede lancering is volledig onafhankelijk van de eerste, daarom is de kans dat 5 in de tweede ook ⅙ is. Dus de gecombineerde kans is:

Kan u van dienst zijn: gedeeltelijke derivaten: eigenschappen, berekening, oefeningen

P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.

Oefening 3

Zoek de kans dat een nummer minder dan 2 uitkomt in de eerste lancering en in de tweede komt er een nummer groter dan 2 uit. 

Oplossing

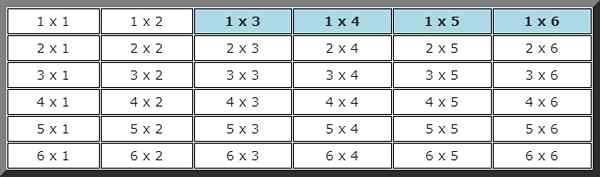
Nogmaals, je moet een mogelijke evenemententabel bouwen, waarbij die waarin de eerste lancering minder dan 2 was en in de tweede hoger dan 2 onderstreept zijn.

In totaal zijn er 4 mogelijkheden van in totaal 36. Met andere woorden, de kans op deze gebeurtenis is:

P (2) = 4/36 = 1/9 = 0.1111 = 11,11%

Met behulp van de waarschijnlijkheidsstelling die stelt:

De kans op het optreden van twee onafhankelijke gebeurtenissen is gelijk aan het product van individuele waarschijnlijkheden.

Het wordt identiek resultaat verkregen:

P (2) = (1/6) (4/6) = 4/36 = 0.1111 = 11,11%

De waarde verkregen met deze procedure valt samen met het vorige resultaat, door de theoretische of klassieke definitie van waarschijnlijkheid.

Oefening 4

Wat is de kans dat door het lanceren van twee gezien de som van de waarden 7 is.

Oplossing

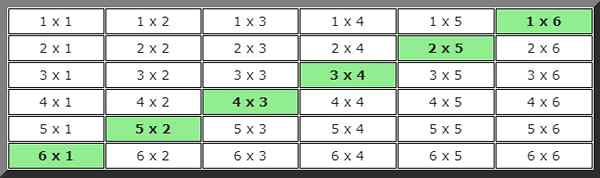
Om de oplossing in dit geval te vinden, is een beeld van mogelijkheden ontwikkeld waarin de gevallen die voldoen aan de toestand van de waarden 7 zijn aangegeven in kleur.

Kijkend naar de tabel kunnen 6 mogelijke gevallen worden geteld, dus de kans is:

P (R&D II: 7) = 6/36 = 1/6 = 0.1666 = 16,66%

Referenties

1. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
2. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
3. Lipschutz, s. 1991. Schaum -serie: waarschijnlijkheid. McGraw Hill.
4. Obregón, ik. 1989.Theorie van waarschijnlijkheid. Redactionele limusa.
5. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.