Vierkante prisma

We leggen uit wat een vierhoekig prisma is, de kenmerken, gezichten, hoekpunten, randen, hoe het volume, voorbeelden en oefeningen te berekenen opgelost

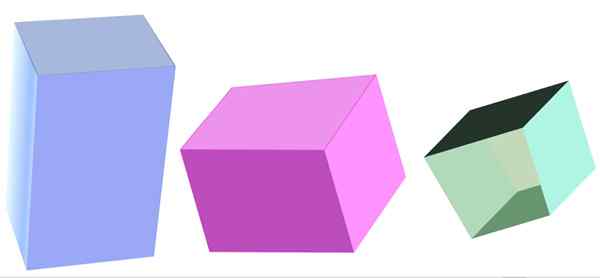
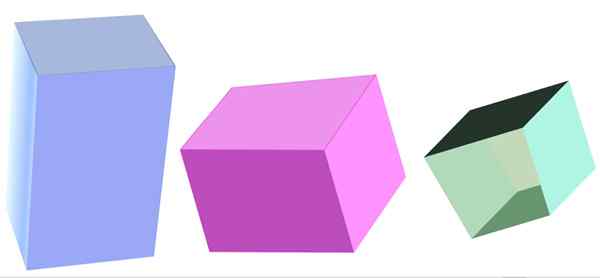Verschillende soorten vierhoekig prisma. Bron: f. Zapata

Wat is een vierhoekig prisma?

Hij Vierkante prisma Het is een drie -dimensionale geometrische figuur van de Polyhedros -familie. Het bestaat uit twee gelijke en parallelle gezichten, met de vorm van een vierhoek, als basis, en vier parallellogrammen aan de zijkanten, voor een totaal van zes gezichten.

Er zijn verschillende criteria om ze te classificeren, omdat er veel mogelijkheden zijn voor de vorm van gezichten en neiging. Er zijn bijvoorbeeld Rechtstreeks naar huis run prisma's en de hellende vierhoekige prisma's.

In het eerste geval staan ​​de zijkanten loodrecht op de basis, en dan zijn ze rechthoeken of vierkanten. In het tweede geval zijn de zijvlakken geneigd met betrekking tot de basis, daarom kunnen ze niet rechthoeken of vierkant zijn.

Bovendien kan vierhoekig prisma regelmatig of onregelmatig zijn, afhankelijk van de basis is een normale of onregelmatige vierhoek. Het reguliere vierhoek is het vierkant, waarvan de vier zijden en zijn vier hoeken hetzelfde meten .

Een voorbeeld van speciaal thuisrun -prisma is de parallellepiped, wiens bases parallellogrammen zijn. De vormen van de dozen en bakstenen zijn geïnspireerd door vierhoekige prisma's, dus goede voorbeelden van hoe deze geometrische figuur in praktische toepassingen te gebruiken zijn.

Kenmerken van het vierhoekige prisma

Een van de belangrijkste kenmerken van het vierhoekige prisma zijn de volgende:

• Hun gezichten hebben een polygoonvorm.
• Het heeft in totaal 6 gezichten (2 basen en 4 zijden), 12 randen of randen en 8 hoekpunten (hoeken).
• De zijvlakken kunnen de vorm hebben van: vierkant, rechthoek, parallellogram, rhombus of rhomboid.
• De zijkanten kunnen recht zijn (vorm 90º hoek met de basen) of hellend (er is een hoek minder dan 90º aan de interne zijde).
• De laterale gezichten van rechte prisma's kunnen alleen vierkant of rechthoeken zijn.
• De prismabases ontvangen ook de naam van richtlijnen.
• Als de basis regelmatig vierhoek is, is het vierhoekige prisma ook regelmatig. Aangezien een platte figuur regelmatig is als alle zijden dezelfde maatregel hebben, is de enige mogelijkheid dat de bases vierkant zijn.
• Wanneer de basis van het prisma enig ander vierhoek is anders dan het plein, dan wordt het prisma beschouwd als onregelmatig.
• Het reguliere vierhoekige prisma kan in een cilinder worden geregistreerd.

Kan u van dienst zijn: Inferentiële statistieken: geschiedenis, kenmerken, waarvoor is het voor voorbeelden

Elementen van het vierhoekige prisma

De vijf elementen van het vierhoekige prisma zijn gemeenschappelijk voor alle prisma's:

• Honken, gevormd door twee identieke en parallelle vierhoek.
• Laterale gezichten, zijn de vier parallellogrammen die de figuur grenzen.
• Hoekpunten of hoeken, gemeenschappelijke punten met drie aangrenzende zijden van het prisma.
• Randen of randen, gemeenschappelijk segment dat twee aangrenzende gezichten heeft.
• Hoogte: Het is de lengte van een loodrecht segment met uiteinden in de basen. Wanneer het prisma recht is, valt de hoogte samen met de maat van de laterale randen.
• Rechte sectie, Gebied van het snijvlak tussen het prisma en een vlak dat 90º vormt met de zijranden.

De volgende afbeelding toont elk van deze elementen voor een recht vierhoekig prisma:

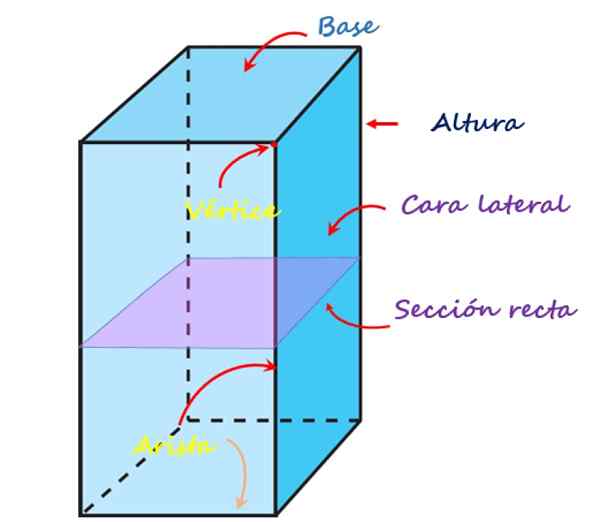De elementen van het vierhoekige prisma. Bron: f. Zapata

Gezichten, hoekpunten en randen

Van groot belang om het vierhoekige prisma te bestuderen zijn de gezichten, de hoekpunten en de randen:

Gezichten

De gezichten van het prisma maken een totaal van 6: de 2 identieke basen in de vorm van een vierhoek en de 4 zijkanten of gezichten in de vorm van parallellogram.

Hoekpunten

Ze zijn de hoeken van de figuur, het punt waar drie aangrenzende gezichten komen.

Randen

Het zijn de snijgmenten tussen het prisma -gezichten. De randen zijn geclassificeerd als:

• Basisranden, Veel voorkomende segmenten tussen bases en zijgezichten.
• Laterale randen, Zoals de naam al aangeeft, zijn het de gemeenschappelijke segmenten tussen de zijgezichten.

De bovenste figuur toont de twee soorten randen, aangeduid met verschillende kleurpijlen. Het aantal randen n_NAAR kan worden bepaald met de Euler Stelling van de polyhedros, die het aantal randen relateert aan dat van gezichten n_C en hoekpunten n_V:

Kan u van dienst zijn: wiskundige functies

N_NAAR = N_C + N_V −2

Voor het vierhoekige prisma n_C = 6 en n_V = 8, daarom:

N_NAAR = 6 + 8 −2 = 12

Daarom is het aantal randen of randen van het vierhoekige prisma 12.

Hoe het volume van een vierhoekig prisma te berekenen?

Het volume van het prisma wordt opgevat als het deel van de door hem vergrendelde ruimte en wordt gemeten in kubieke eenheden, die kubieke meter, kubieke centimeter, kubieke voet of andere geschikte kunnen zijn, op voorwaarde dat ze van lengte zijn voor de kubus.

Deel V is altijd een positieve hoeveelheid, en in het geval van een vierhoekig prisma wordt het door het product tussen de basis van de basis gegeven aan_B en hoogte h:

V = a_B × h

Yo) Regelmatig vierhoekig prisma -volume

Omdat de bases vierkant zijn en het vierkant van het vierkant zijn zijde ℓ vierkant:

NAAR_B = ℓ²

Dan is het volume van het prisma waarvan de hoogte "H" is:

V = ℓ² × h

Ii) Onregelmatig vierhoekig prisma -volume

Het hangt af van de vorm van de basis en de hoogte "H" van het prisma:

1.- Rechthoekige basis prisma

Het gebied van de zijkanten rechthoek "A" en "B" is:

NAAR_B = A × B

Dus het volume is:

V = a × b × h

2.- Romboidal Base Prism

Het Rhombus -gebied is het semi -product van zijn "D" en "D" diagonalen:

En het volume is:

3.- Romboid -vormige basis prisma

Het rhomboid -vormige basisgebied is het product van zijn basis "B" en zijn relatieve hoogte "H_R"Naar deze basis, het loodrechte segment dat van deze basis naar de parallelle kant gaat.

NAAR_B = B × H_R

Daarom is het volume van het prisma met deze basis:

Kan u van dienst zijn: wat is de statistiekenbereik? (Met voorbeelden)

V = b × h_R × h

4.- Trapeziumvormige basisprisma

Omdat het gebied van de trapezoid de semi -plaats van de parallelle zijkanten "A" en "B" is, vermenigvuldigd met zijn hoogte "C":

Het volume van het trapeziumvormige prisma is:

5.- Trapezoid -vormige basis prisma

Het gebied van een symmetrische trapezium is het semi -product van zijn diagonalen D en D, daarom:

In dit geval is het volume van het prisma:

Oefening opgelost

Een trapeziumvormige vierhoekig prisma heeft een volume van 648 cm³. De parallelle zijkanten van de trapezoid maat a = 10 cm en b = 5 cm, terwijl de hoogte van de trapeze c = 6 cm is. Vind met deze gegevens de hoogte van de prisma.

Oplossing

Omdat de afmetingen van de basis hebben, kan uw gebied gemakkelijk worden berekend:

En van de formule:

V = a_B × h

"H" wordt gewist, de hoogte van het prisma, omdat het volume bekend is:

H = v/ a_B = 648 cm³ / 45 cm² = 14.4 cm

Voorbeelden

Rechthoekig prisma of kubus

De zes gezichten van dit rechte prisma zijn vierkant of rechthoekig. De dozen zijn voorbeelden van rechthoekige prisma's, een vorm die ook wordt gebruikt in tal van objecten en constructies zoals gebouwen.

Kubus

Een kubus is een regelmatig vierhoekig prisma, waarvan de zes zijden de vorm hebben van een vierkant, bijvoorbeeld een dobbelsteen of het goed bekende Rubik's Cube -spel.

De kubus maakt deel uit van de groep platonische vaste stoffen, geometrische figuren die aan twee voorwaarden voldoen. De eerste is dat elk gezicht een normale polygoon is en de tweede is dat elk hoekpunt hetzelfde aantal gezichten gemeen heeft.

De kubus voldoet aan beide omstandigheden, omdat hun gezichten een vierkante vorm hebben, wat een gewone polygoon is. En in elk van de acht hoekpunten van de kubus drie gezichten van dezelfde converge.

De resterende platonische vaste stoffen zijn de tetraëder, de octaëder, de dodecaëder en de icosaedro.