Relatieve neven en nichten wat zijn, uitleg, voorbeelden

Wordt genoemd Relatieve neven en nichten (Coprmimos of neven ten opzichte van elkaar) tot een paar hele getallen die geen gemeenschappelijke deler hebben, behalve 1. Met andere woorden, twee hele getallen zijn relatieve neven en nichten als ze in hun uitsplitsing in priemgetallen geen gemeenschappelijke factor hebben.

Als de 4 en 25 bijvoorbeeld worden gekozen, zijn de ontledingen in topfactoren van elk respectievelijk 2² en 5². Zoals te zien is, hebben ze geen gemeenschappelijke factor, daarom zijn 4 en 25 relatieve neven en nichten.

Aan de andere kant, als u 6 en 24 kiest, bij het afbreken van de prime -factoren wordt verkregen dat 6 = 2*3 en 24 = 2³*3.

Zoals te zien is, hebben deze laatste twee uitdrukkingen ten minste één gemeenschappelijke factor, daarom zijn het geen relatieve neven en nichten.

Kenmerken van relatieve neven en nichten

Een detail waarmee zorg moet.

Aan de andere kant kan de bovenstaande definitie als volgt worden samengevat: twee gehele getallen "a" en "b" zijn relatieve neven en en alleen de maximale gemeenschappelijke deler hiervan is 1, dat wil zeggen mcd (a, b ) = 1.

Twee onmiddellijke conclusies van deze definitie zijn dat:

-Als "a" (of "b") een priemgetal is, dan mcd (a, b) = 1.

-Als "A" en "B" priemgetallen zijn, dan MCD (A, B) = 1.

Dat wil zeggen, als ten minste een van de gekozen nummers een priemgetal is, dan zijn het paar getallen relatieve neven en nichten.

Andere mogelijkheden

Andere resultaten die worden gebruikt om te bepalen of twee nummers relatieve neven en nichten zijn:

-Als twee hele getallen opeenvolgen zijn, zijn dit relatieve neven en nichten.

-Twee natuurlijke getallen "A" en "B" zijn relatieve neven en alleen als, en alleen als, de cijfers "(2^a) -1" en "(2^b) -1" zijn relatieve neven en nichten.

-Twee hele getallen "A" en "B" zijn relatieve neven en nichten als, en alleen als, bij het in kaart brengen van het punt (A, B) in het Cartesiaanse vlak, en de lijn bouwen die door de oorsprong (0.0) en (A gaat B), dit bevat geen enkel punt met volledige coördinaten.

Voorbeelden

1.- Overweeg hele getallen 5 en 12. De ontledingen in topfactoren van beide getallen zijn respectievelijk: 5 en 2²*3. Concluderend zijn MCD (5,12) = 1 daarom 5 en 12 relatieve neven en nichten.

2.- Laat de nummers -4 en 6. Dan -4 = -2² en 6 = 2*3, zodat de MCD (-4,6) = 2 ≠ 1. Concluderend -4 en 6 zijn geen relatieve neven en nichten.

Als de lijn die door de geordende paren gaat (-4,6) en (0,0) en om de vergelijking van deze lijn te bepalen, kan worden geverifieerd dat dit door het punt gaat (-2,3).

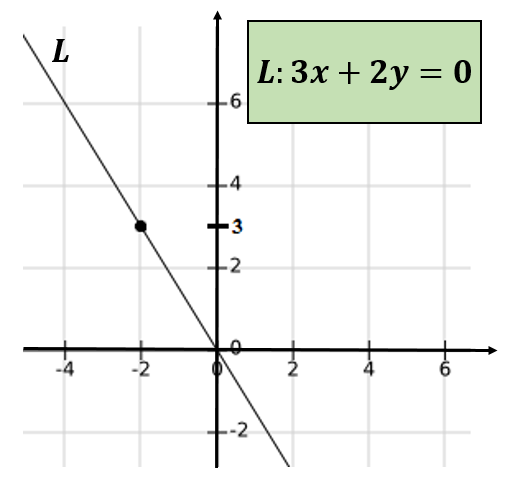
Nogmaals, er wordt geconcludeerd dat -4 en 6 geen relatieve neven en nichten zijn.

3.- Nummers 7 en 44 zijn relatieve neven en kunnen snel worden gesloten dankzij wat hierboven is gezegd, omdat 7 een priemgetal is.

4.- Overweeg nummers 345 en 346. Als twee opeenvolgende getallen, wordt geverifieerd dat MCD (345,346) = 1 daarom 345 en 346 relatieve neven en nichten zijn.

5.- Als nummers 147 en 74 worden overwogen, zijn dit relatieve neven en nichten, aangezien 147 = 3*7² en 74 = 2*37, daarom de MCD (147,74) = 1.

6.- Numeri 4 en 9 zijn relatieve neven en nichten. Om het aan te tonen, kunt u de hierboven genoemde tweede karakterisering gebruiken. Inderdaad, 2^4 -1 = 16-1 = 15 en 2^9-1 = 512-1 = 511.

De verkregen cijfers zijn 15 en 511. De ontledingen in topfactoren van deze getallen zijn respectievelijk 3*5 en 7*73, zodat MCD (15.511) = 1.

Zoals u kunt zien, is het gebruik van de tweede karakterisering een langer en moeizame werk om het direct te verifiëren.

7.- Overweeg de nummers -22 en -27. Vervolgens kunnen deze getallen als volgt worden herschreven: -22 = -2*11 en -27 = -3³. Daarom zijn de MCD (-22, -27) = 1, dus -22 en -27 relatieve neven en nichten.