Eerste balansvoorwaarde Verklaring, voorbeelden, oefeningen

De Eerste balansvoorwaarde Het vereist dat de sumptorische vector van alle krachten die op een lichaam werken, nietig is, zodat deze in rust is (statische balans) of met uniforme rechtlijnige beweging (dynamisch evenwicht).

Deze som van krachten is niemand minder dan de netto kracht die op het lichaam werkt en deze modus wiskundig uitdrukt:

F_Netto = 0

∑ F = 0

Figuur 1. De bouwers van de oudheid hebben al de eerste evenwichtstoestand toegepast, zoals blijkt uit het Stonehenge -monument. Bron: Pixabay.

In de ruimte geeft de eerste evenwichtstoestand aanleiding tot drie vergelijkingen, één voor elke dimensie:

∑ f_X = 0; ∑ f_En = 0 en ∑ f_Z = 0

Wanneer aan deze vergelijkingen is voldaan, beweegt het object niet of als dit het geval is, zal het met constante snelheid zijn.

Om ons heen observeren we ons realiseren ons dat we voortdurend proberen de eerste balansvoorwaarde te bevredigen, zodat dingen niet vallen.

Daarom wil het de zwaartekrachtaantrekking van de aarde compenseren door ondersteuning, touwen of ondersteuning van sommigen, zodat dingen op hun plaats blijven en niet naar de grond gaan.

Andere keren wat nodig is, is om te voorkomen dat externe elektromagnetische velden de werking van elektrische circuits en communicatieapparaten verstoren. In dat geval zijn het de elektrische ladingen die in evenwicht moeten zijn.

[TOC]

Voorbeelden

Een groot aantal alledaagse voorwerpen voldoet aan de eerste evenwichtstoestand, het is een kwestie van zorgvuldig observeren:

Gebouwen

Bouwers zoeken stabiliteit in constructies zodat gebruikers veilig blijven. Het doel van statisch is het bestuderen van de voorwaarden voor statisch evenwicht in gebouwen, bruggen, wegen en allerlei structuren.

Higaforen en hangende waarschuwingen

Deze signaalapparaten moeten vast blijven om hun functies te vervullen, daarom zijn ze onderworpen aan kabels, posten en staven op een zodanige manier dat aan de eerste balansvoorwaarde wordt voldaan.

Het kan u van dienst zijn: Derde wet van thermodynamica: formules, vergelijkingen, voorbeeldenFiguur 2. Verkeerslichten en hangende waarschuwingen zijn zo onderworpen dat het voldoet aan de eerste evenwichtstoestand. Bron: PxFuel.

Elektrost balans stuurprogramma'spenthouse

Wanneer geleidende materialen zoals koper en andere metalen elektrische lading verwerven, wordt de elektrostatische balans binnenkort vastgesteld, waardoor het belastingoverschot op het geleidende oppervlak blijft. In het elektrische veld is nul.

Dit effect wordt vaak gebruikt om elektrische en elektronische apparatuur van de externe velden te isoleren, door middel van de So -called Faraday Cage. De kooi is gemaakt van geleidend materiaal en omringt de te beschermen apparatuur.

Tijdens stormen dienen auto's als Faraday -kooien door inzittenden te beschermen tegen elektrische schokken.

Plafondlampen

In verlichtingssystemen, zoals hangende lampen, wordt de eerste balansconditie gebruikt om ze op het dak, op de vloer of de muur te repareren.

figuur 3. De uitgebreide daklamp genaamd "Spiders" voldoet aan de eerste evenwichtstoestand. Bron: Pixabay.

Boeken en objecten op tabellen

De objecten die op tabellen en planken worden geplaatst, voldoen aan de eerste balansconditie. De normale kracht die de ondersteuning op de objecten uitoefent, is verantwoordelijk voor het compenseren van het gewicht.

Maat voor de viscositeit van een vloeistof

Om de viscositeit van een vloeistof een bolvormig object te bepalen, met een bekende diameter, die de snelheid ervan zal zien vanwege de weerstand is binnenin gevallen. De snelheid van de bol is constant, in dynamisch evenwicht.

Een grotere viscositeit van de vloeistof, minder de snelheid waarmee de bol naar binnen beweegt.

Stappen om de eerste evenwichtstoestand toe te passen

-Maak een vrij lichaamsdiagram, dat alle krachten toont die op het lichaam werken (laat weg wat het lichaam op anderen uitoefent).

Het kan je van dienst zijn: natuurkunde in de middeleeuwen

-Selecteer een Cartesiaans coördinatensysteem en zorg ervoor dat de krachten indien mogelijk zich op een van de assen bevinden. Het positieve adres wordt meestal genomen in de zin van beweging of een mogelijke beweging.

-Bepaal de Cartesiaanse componenten van elke kracht.

-Pas de tweede wet van Newton toe voor elke component, zoals in het begin vastgesteld, er is een systeem van vergelijkingen.

-Los het systeem van vergelijkingen op die in de vorige stap zijn verhoogd los.

Opgeloste oefeningen

- Oefening opgelost 1

Het blok van de figuur, van massa M, Het beweegt bergafwaarts op het hoekvlak θ met constante snelheid. Bereken de waarde van de kinetische wrijving μ -coëfficiënt_k, Als de massa van het blok m = 5 kg is en θ = 37º.

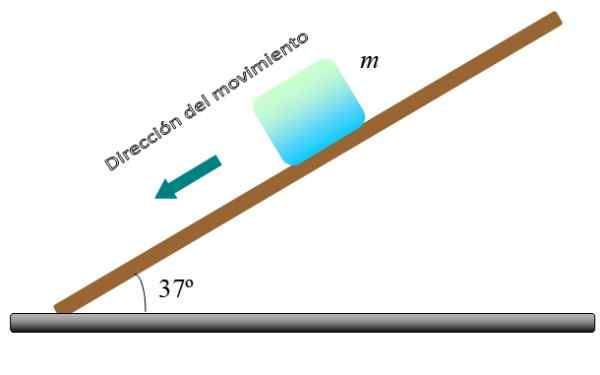Figuur 4. Een blok glijdt met constante snelheid op een hellend vlak. Bron: f. Zapata.

Oplossing

De eerste stap is om het vrije lichaamsdiagram te tekenen en een Cartesiaans coördinatensysteem te kiezen om elke krachtvector uit te drukken. De krachten die op het blok handelen zijn:

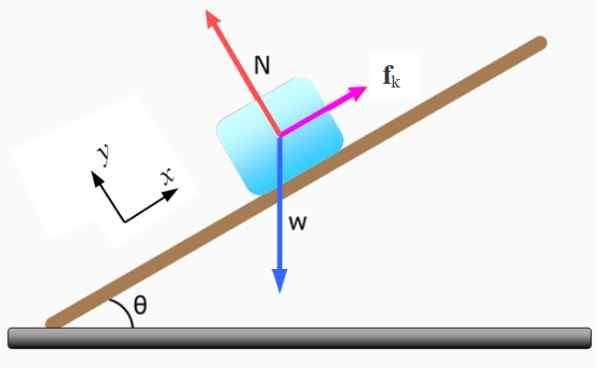Figuur 5. Gratis lichaamsdiagram voor blok. Bron: f. Zapata.

-De normale N uitgeoefend door het hellende vlak, het staat loodrecht op het oppervlak hiervan.

-Het gewicht W Het wordt verticaal gericht.

-Kinetische wrijving F_k Dat verzet zich tegen beweging. Als het niet zou bestaan, zou het lichaam bergafwaarts bewegen met een versnelling gelijk aan G.Senθ.

Als gewicht W Het is geneigd met betrekking tot de geselecteerde coördinaatassen, het moet worden opgesplitst in zijn Cartesiaanse componenten:

W_X = Mg.Sen 37º = 5 kg x 9,8 m/s² x sin 37º = 29. 5 n
W_En = Mg.cos 37º = 5 kg x 9,8 m/s² x cos 37º = 39.1 n

De tweede wet van Newton wordt nu toegepast en komt overeen met elke som op 0, omdat het blok versnelling mist bij het beweegt met constante snelheid:

∑ f_En = N - W_En = 0
∑ f_X = W_X - F_k = 0

De grootte van kinetische wrijving is evenredig met de grootte van het normaal, is de kinetische wrijvingscoëfficiënt μ_k De evenredigheid constant.

Het kan u van dienst zijn: absolute druk: formule, hoe het wordt berekend, voorbeelden, oefeningen

F_k = μ_k N

Tegelijkertijd:

N = W_En = 39.1 n

En ook:

F_k = W_X

Daarom:

29. 5 n = μ_k X 39.1 n

μ_k = 29. 5/39.1 = 0.75

- Oefening opgelost 2

Bereken de grootte van de spanningen die het massa -verkeerslicht 33 kg ondersteunen, weergegeven in de figuur:

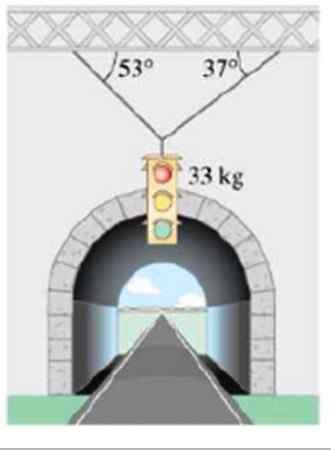Figuur 6. Een verkeerslicht hangt met kabels. Bron: Giancoli. Fysica met toepassingen.

Oplossing

Het vrije lichaamsdiagram wordt zowel gedaan voor het verkeerslicht als voor de knoop die de kabels vasthoudt:

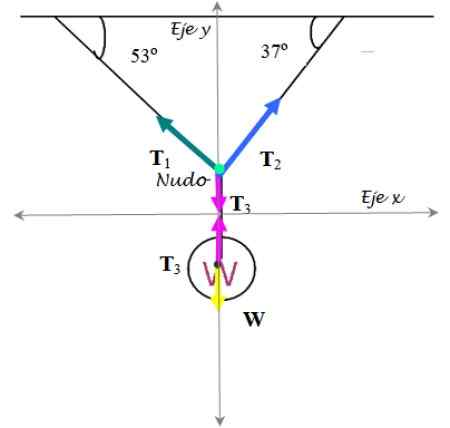Figuur 7. Gratis lichaamsdiagram voor de oefening opgelost 2. Bron: f. Zapata.

Stoplicht

Over het handelen: de spanning t₃ omhoog en gewicht w beneden. Daarom:

∑ f_En = W - t₃ = 0

Daarom:

T₃ = 33 kg x 9.8 m/s² = 323.4 n

Knoop

Spanningen gaan af in hun Cartesiaanse componenten:

∑ f_En = T₁ Sen 53º + T₂ Sen 37º - T₃ = 0
∑ f_X = T₂ Cos 37º - t₁ Cos 53º = 0

En het volgende systeem van lineaire vergelijkingen met twee onbekenden wordt verkregen₁  en t₂ :

- 0.6 t₁ + 0.8 t₂ = 0
0.8 t₁ + 0.6 t₂ = 323.4

De oplossing van dit systeem van vergelijkingen is: t₁ = 258.7 N en T₂ = 194.0 n

Thema's van belangstelling

Evenwichtsvoorwaarden.

Tweede evenwichtstoestand.

Referenties

1. Bedford, 2000. NAAR. Mechanica voor engineering: statisch. Addison Wesley.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 4. Deeltjessystemen. Uitgegeven door Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.
5. Wikipedia. Statisch (mechanisch). Hersteld van: is.Wikipedia.borg.