Regelmatige polygonenigenschappen, elementen, hoeken, voorbeelden

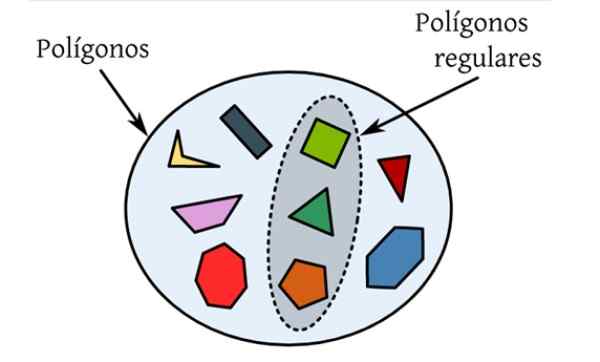
De Regelmatige polygonen Zij zijn degenen die al hun kanten en hun gelijke interne hoeken hebben. In de volgende figuur zijn er een set verschillende polygonen, die vlakke cijfers zijn die beperkt zijn door een gesloten curve en alleen die welke worden gemarkeerd, voldoen aan de te reguliere omstandigheden.

De gelijkzijdige driehoek is bijvoorbeeld een normale polygoon, omdat de drie zijden hetzelfde meten, evenals de interne hoeken, die elk 60 º waard zijn.

Figuur 1. Regelmatige polygonen zijn die wiens zijden en interne hoeken hetzelfde zijn, zoals de gelijkzijdige driehoek en het vierkant. Bron: Wikimedia Commons.

Het vierkant is een vierhoek met vier zijden van gelijke maatregel en waarvan de interne hoeken 90º zijn. Het wordt gevolgd door het reguliere Pentagon, met vijf zijden van gelijke grootte en vijf interne hoeken van elk 108º.

Wanneer een polygoon regelmatig is, wordt dit woord toegevoegd aan zijn speciale naam, dus hebben we de reguliere zeshoek, de reguliere heptagon enzovoort.

[TOC]

Eigenschappen van gewone polygonen

De belangrijkste eigenschappen van reguliere polygonen kunnen als volgt worden samengevat:

-De zijden meten hetzelfde, daarom zijn ze dat equilaterals.

-Zijn Gelijkwaardig, Nou, al zijn interne hoeken hebben gelijke maatregel.

-Ze kunnen zich altijd in een omtrek registreren, wat betekent dat ze perfect in één passen, die wordt genoemd, die wordt genoemd omschreven omtrek.

-Voor een normale polygoon van N -zijden is de maat van een binnenhoek α:

α = [180 (n-2)]/n

-N-3)/2 diagonalen kunnen worden getrokken uit de hoekpunten van een polygoon, nu regelmatig of niet.

-De som van Buitenhoeken Het is gelijk aan 360º.

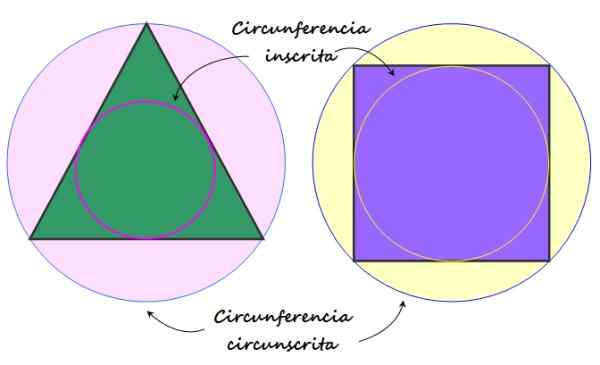Figuur 2. Geregistreerde omtrek en omtrek omschreven naar de reguliere polygoon. Bron: f. Zapata.

Elementen van een gewone polygoon

Vervolgens presenteren we de belangrijkste elementen van een gewone polygoon, gevisualiseerd in de onderste figuur.

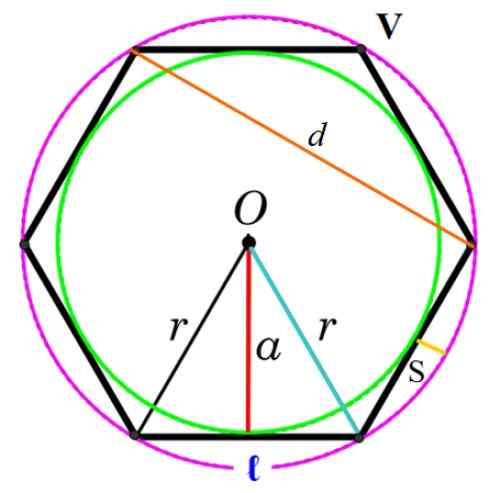figuur 3. Elementen van de reguliere polygoon. Bron: f. Zapata.

Hoekpunt

Gemeenschappelijk punt dat twee opeenvolgende kanten heeft, aangeduid als V in de figuur.

Kant

Het is het segment dat twee opeenvolgende hoekpunten van de polygoon verbindt en wordt aangeduid als ℓ of l.

Diagonaal

Segment dat samenkomt D.

Centrum

Het is het gemeenschappelijke centrum van de geregistreerde omtrek en de omschreven omtrek, aangegeven door de letter of. Het kan ook worden gezien als het enige punt dat equidista van zowel de hoekpunten als de middelpunten aan elke kant.

Radio

Het is de radio R van de omschreven omtrek en valt samen met de afstand tussen O en een hoekpunt.

Het kan u van dienst zijn: Axioma van waarschijnlijkheid: typen, uitleg, voorbeelden, oefeningen

Apothem

Het heet Apothem naar de straal van de omtrek ingeschreven in de polygoon, weergegeven in de figuur met een letter naar. De apothem staat loodrecht op de zijkant en verenigt dit met het midden O (rood segment in figuur 3).

Als je de straal R en de lengte van de zijkant kent, wordt de apothem berekend door:

Omdat de apothem in feite een van de categorieën van een rechthoekige driehoek is (zie figuur 3), is de andere cateto de waarde van ℓ/2 (de helft van de ene zijde) en de hypotenuse de radio R van de polygoon.

Wanneer de Pythagoras -stelling wordt toegepast op de genoemde driehoek, wordt deze vergelijking verkregen, die niet alleen geldig is voor de zeshoek, maar voor een reguliere polygoon.

Centrale hoek

Het is de hoek waarvan de hoekpunt samenvalt met het midden of waarvan de zijden de segmenten zijn die het centrum verenigen met twee opeenvolgende hoekpunten. De maatstaf in seksuele graden is 360º/N, waar N Het is het aantal zijden van de polygoon.

Sagita

Het is het verschil tussen de straal van de polygoon en de apothem (zie figuur 3). Sagita aangeven als s:

S = R - A

Perimeter en gebied

Omtrek

Het wordt gemakkelijk berekend door de lengte van de zijkanten toe te voegen. Aangezien elke kant dezelfde lengte L is en er n zijkanten zijn, wordt de omtrek P uitgedrukt als:

P = n.L

Gebied

In een normale polygoon wordt het gebied A gegeven door het product tussen de semi-perimeter (de helft van de omtrek) en de apotheme lengte naar.

A = P.A /2

Aangezien de omtrek afhangt van het aantal zijden n, blijkt dat:

A = (NL).A /2

Twee gewone polygonen kunnen dezelfde omtrek hebben, zelfs als ze niet hetzelfde aantal zijden hebben, omdat het dan zou afhangen van de lengte van de zijkanten.

In boek V van uw Verzameling, De wiskundige pappus van Alexandrië (290-350), de laatste van de grote Griekse wiskundigen van de oudheid, toonde aan dat onder alle reguliere polygonen met dezelfde omtrek, degene met het grootste gebied het is met het grootste aantal kanten.

Hoeken

Figuur 4 toont de relevante hoeken in een normale polygoon, aangeduid met de Griekse letters α, β en γ.

Centrale hoek

Eerder noemen we de centrale hoek, onder de elementen van de reguliere polygoon, het is de hoek waarvan het hoekpunt zich in het midden van de polygoon bevindt en de zijkanten de segmenten zijn die het midden verenigen met twee opeenvolgende hoekpunten.

Om de maat van de centrale hoek α te berekenen, wordt 360º gedeeld door N, het aantal zijden. Of 2π radialen tussen n:

Kan u van dienst zijn: injectieve functie: waar het uit bestaat, waarvoor is het en voorbeelden

α = 360º/n

Equivalent in radialen aan:

α = 2π /n

Interne hoek of binnenhoek

In figuur 4 is de interne hoek β degene waarvan de hoekpunt samenvalt met een van de figuur en de zijkanten zijn ook zijden van de figuur. Het wordt berekend in seksuele graden door:

β = [180 (n-2)]/n

Of in radialen gebruiken:

β = [π (n-2)]/n

Externe hoeken

Ze worden aangeduid met de Griekse letter γ. In de figuur wordt waargenomen dat γ + β = 180º. Daarom:

γ = 180º - β

De som van alle externe hoeken naar een gewone polygoon is 360º.

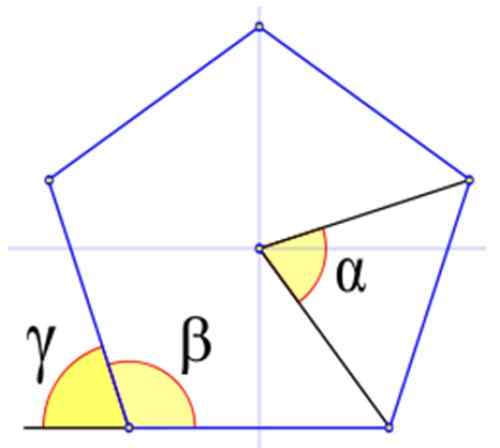Figuur 4. De hoeken in een gewone polygoon, in dit voorbeeld een gewone Pentagon. Bron: Wikimedia Commons.

Voorbeelden van gewone polygonen

Hieronder hebben we de eerste 8 gewone polygonen. We zien dat naarmate het aantal zijden toeneemt, de polygoon steeds meer wordt naar de omtrek waarin ze zijn geregistreerd.

We kunnen ons voorstellen dat we de lengte van de zijkanten steeds kleiner worden, en het verhogen van het aantal hiervan, we krijgen de omtrek.

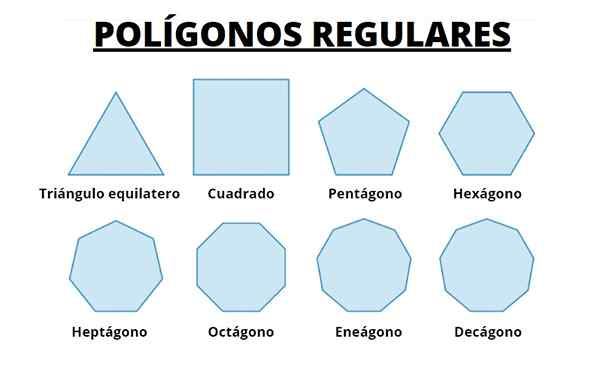Figuur 5. De eerste acht reguliere polygonen. Bron: Wikimedia Commons.

- Regelmatige polygonen in het dagelijks leven en de natuur

Regelmatige polygonen worden overal in het dagelijks leven gevonden en zelfs in de natuur. Laten we eens kijken naar enkele voorbeelden:

Verkeerssignalen

In de bewegwijzering zien we op snelwegen en wegen in overvloed gewone polygonen zoals gelijkzijdige, vierkante en rhombus -driehoeken. In figuur 6 zien we een signaalsignaal met hoge vorm.

Figuur 5.- Verkeerslicht met een achthoekige vorm. Bron: Pixabay.

Meubilair

Ontelbare meubelstukken zijn bijvoorbeeld vierkant, als een karakteristieke geometrische figuur, evenals vele tafels, stoelen en banken zijn vierkant. Een parallellepiped is over het algemeen een doos met rechthoekige kegelzijden (die geen gewone polygoon is), maar ze kunnen ook vierkant maken.

Architectuur en constructie

De tegels of tegels van de vloeren en muren, zowel in huizen als op straat, hebben vaak de vorm van gewone polygonen.

De Tesels zijn oppervlakken die volledig worden bedekt met tegels met verschillende geometrische figuren. Met de driehoek kunnen het vierkant en de zeshoek regelmatig teten worden gemaakt, die die slechts één type figuur gebruiken om perfect te coaten, zonder lege spaties (zie figuur 6).

Ook maken de gebouwen gebruik van gewone polygonen in elementen zoals ramen en decoratie.

Figuur 6. Vierkante tegel. Bron: Pixabay.

- Regelmatige zeshoeken in de natuur

Verrassend genoeg is gewone zeshoek een veelhoek die vaak in de natuur verschijnt.

Kan u van dienst zijn: discrete distributies

Honingraat gemaakt door bijen om honing op te slaan, hebben een zeer geschatte vorm voor een gewone zeshoek. Zoals de pappus van Alexandrië opmerkte, optimaliseren op deze manier de ruimte om zoveel mogelijk honing te besparen.

En er zijn ook gewone zeshoeken in de schaal van schildpadden en sneeuwvlokken, die ook verschillende zeer mooie geometrische vormen aannemen.

Oefening opgelost

Een gewone zeshoek maakt deel uit van een halve cirkel van 6 cm straal, zoals getoond in de figuur. Wat is de waarde van het gearceerde gebied?

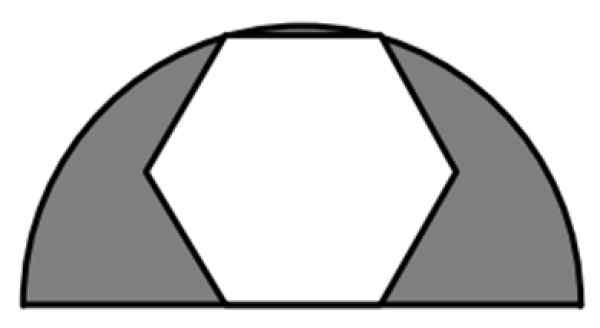Figuur 7. Een gewone zeshoek geregistreerd in een halve cirkel. Bron: f. Zapata.

Oplossing

Het gearceerde gebied is het verschil tussen de straal semicircle -oppervlakte r = 6 cm en het volledige zeshoekige gebied, een gewone 6 -zijdige polygoon. Dus we hebben formules nodig voor het gebied van elk van deze figuren.

Halve cirkelvormige gebied

NAAR₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Regelmatig zeshoekig gebied

De formule voor het berekenen van het gebied van een gewone polygoon is:

A = P.A /2

Waar P Het is de omtrek en naar Het is de apothem. Aangezien de perimeter de som van de zijkanten is, hebben we de waarde hiervan nodig. Voor gewone zeshoek:

P = 6ℓ

Daarom:

A = 6ℓA /2

Om de waarde van de zijde te vinden ℓ ℓ is het noodzakelijk om hulpcijfers te bouwen, die we hieronder zullen uitleggen:

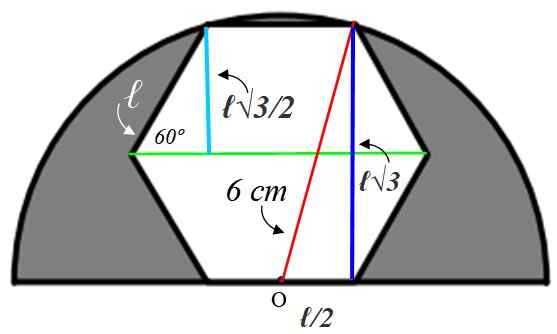
Laten we beginnen met de kleine rechthoekige driehoek naar links, waarvan de hypotenuse is ℓ. Een interne invalshoek van de zeshoek is waard:

α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120º

De straal die we in Bisecta Green hebben getrokken deze hoek, daarom is de acute hoek van de kleine driehoek 60º. Met de verstrekte informatie wordt deze driehoek opgelost, waarbij de lichtblauwe kant wordt gevonden, die hetzelfde meet als de apothem:

Tegenover cateto = a = ℓ x sin 60º = ℓ√3 / 2 cm

Deze waarde is twee keer de donkerblauwe been van de grote driehoek aan de rechterkant, maar vanuit die driehoek weten we dat de hypotenuse 6 cm meet omdat het de straal van de halve cirkel is. De resterende cateto (hieronder) is waard ℓ/2 omdat het punt of in het midden van de zijkant is.

Omdat interne hoeken van deze driehoek niet bekend zijn, kunnen we de Pythagoras -stelling voor hem verhogen:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

Met deze waarde wordt de apothem berekend:

a = ℓ√3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

Laten we een₂ naar het reguliere zeshoekige gebied:

= 28. 8 cm²

Gearceerd figuurgebied

NAAR₁ - NAAR₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Referenties

1. Baldor, een. 1973. Geometrie en trigonometrie. Midden -Amerikaans cultureel redactioneel.
2. Geniet van wiskunde. Tesels. Hersteld van: geniet van Matimaticas.com.
3. EN. NAAR. 2003. Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
4. Zeshoeken in de natuur. Hersteld van: malvargamath.WordPress.com.
5. Jiménez, r. 2010. Wiskunde II. Geometrie en trigonometrie. Tweede druk. Prentice Hall.
6. Regelmatige polygonen. Hersteld van: maat.engineering.USAC.Edu.GT.
7. Wikipedia. Apothem. Hersteld van: is.Wikipedia.borg.