Zeshoekige piramide

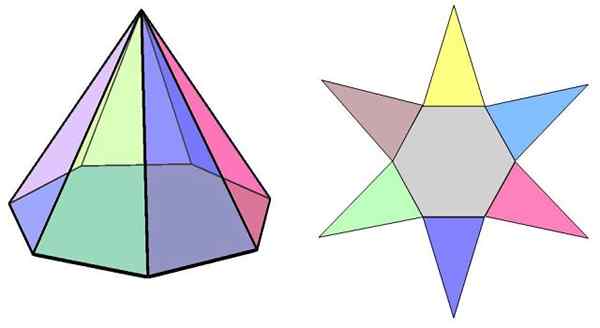Figuur 1. Aan de linkerkant een zeshoekige piramide en rechts, zijn zeven partijen in het vliegtuig ingezet: in het midden de zeshoekige basis en rond de zes driehoekige gezichten. Bron: f. Zapata.

Wat is een zeshoekige piramide?

Een zeshoekige piramide is een drie -dimensionale geometrische figuur, wiens baseren Het is een zeshoek (zeszijdige polygoon) en heeft ook zes gezichten driehoekig, die op een bepaalde hoogte van de basis worden verzameld, op een punt genoemd top of hoekpunt.

In totaal heeft de zeshoekige piramide zeven gezichten als de basis de zijkant van de zijkant is, dus het is ook een polyhedron in de vorm van Heptaëder, woord afgeleid van de Griekse taal ("hept" betekent zeven).

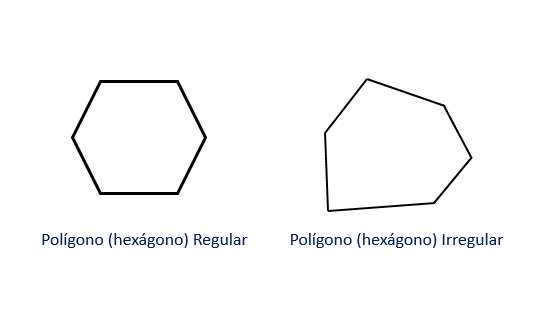
Als de driehoeken die de zijkanten vormen gelijkbenig zijn, dat wil zeggen, ze hebben twee gelijke kanten en een andere, het is een rechte piramide. En als, afgezien daarvan, de zeshoek van de basis regelmatig is, dan is het een gewone zeshoekige piramide, Zoals getoond in figuur 1.

Wanneer de zeshoek van de basis niet regelmatig is, of de driehoeken die de gezichten vormen niet gelijkbenig zijn, is er een Oblicual zeshoekige piramide.

Kenmerken van de zeshoekige piramide

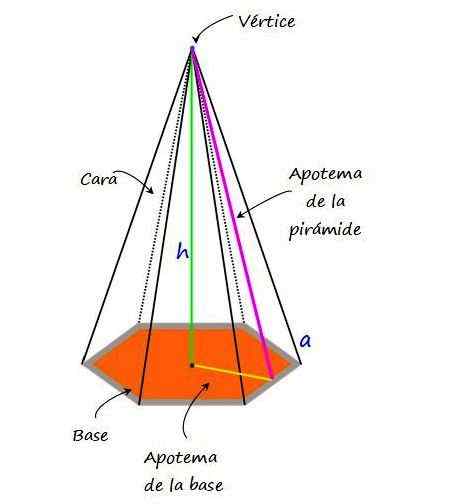Figuur 2.- De zeshoekige piramide en zijn belangrijkste elementen. Bron: f. Zapata.

De belangrijkste kenmerken en elementen van de zeshoekige piramide zijn de volgende:

-Baseren, Het is een zeshoek die regelmatig of onregelmatig kan zijn.

-Gezichten, Ze hebben een driehoeksvorm en totaal van 6.

-Hoekpunt of top van de piramide, toeval van de zes driehoekige gezichten.

-Rand, segment waar twee van de piramide gezichten samenvallen. De Laterale randen Ze zijn de toeval segmenten van de zijzichten, terwijl de randen van de basis de segmenten zijn waar een zijde van de zeshoek samenvalt en een kant van de aangrenzende driehoek. In figuur 2 wordt de rand aangeduid met letter "a".

Kan u van dienst zijn: divisies waarin het residu 300 is

-Hoogte, aangeduid als "h", is het de afstand gemeten vanaf het hoekpunt tot de basis van de piramide.

-Pyramid Apotheme, segment dat zich bij het hoekpunt voegt met het middelpunt aan één kant van de basis.

-Base Apotheme, Het wordt alleen gedefinieerd als de zeshoek regelmatig is. Het bestaat uit een segment dat zich bij het centrum van de zeshoek bij het midden van een van zijn zijden voegt.

Formules voor het gebied en volume

Het oppervlak van de zeshoekige piramide, regelmatig of onregelmatig, wordt berekend door de gebieden van de zijgezichten en het gebied van de zeshoekige basis toe te voegen:

A = A_baseren + ∑a_{duur kant}

In de formule vertegenwoordigt het "∑" -symbool een som, om de som van de zes gebieden van de laterale gezichten samen te vatten.

Voor de reguliere zeshoekige piramide is er een formule om het gebied te vinden:

A = 3L ∙ (AP_baseren + AP_piramide))

Waar:

• L is een rand van de basis (de zijkant van de zeshoek).
• AP_baseren Het is de apothem van de basis
• AP_piramide Het is de apothem van de piramide.

Als de piramide niet regelmatig is, hetzij omdat de basis geen gewone zeshoek is of omdat de piramide schuin is, is het noodzakelijk om de gebieden van elk afzonderlijk te berekenen en vervolgens toe te voegen.

De reguliere zeshoekige piramide heeft ook een formule voor volume:

V = l ∙ AP_baseren∙ H

Hier vertegenwoordigt "H" de hoogte van de piramide.

En als de zeshoekige piramide niet regelmatig is, is er een algemene formule, van toepassing op alle piramides, om het volume te berekenen:

V = ⅓ ∙ a_baseren ∙ H

Het kan u van dienst zijn: ontleding van natuurlijke getallen (voorbeelden en oefeningen)

Numeriek voorbeeld

Voor de reguliere zeshoekige piramide wiens afmetingen zijn:

Base Apothem: 4 cm

Basisrand lengte: 7 cm

Pyramid Apotheme: 15 cm

Hoogte: 10 cm

Bereken het volgende:

a) zeshoekig basisgebied.

b) oppervlakte van de piramide.

c) het volume

Oplossing voor

Het gebied van een gewone zeshoek is:

A = ½ (perimeter × apothema) = ½ (6l × AP_baseren))

A = 3L ∙ AP_baseren  = 3 × 7 cm × 4cm = 84 cm²

Oplossing B

A = 3L ∙ (AP_baseren + AP_piramide) = 3l ∙ AP_baseren  + 3L ∙ AP_piramide = 84 cm² + (3 × 7 cm x 15 cm) = 399 cm².

Oplossing C

Het volume kan worden gevonden door de algemene formule:

V = ⅓ ∙ a_baseren ∙ h = ⅓ ∙ ∙ 84cm² ∙ 10 cm = 280 cm³

Hoe je een zeshoekige piramide maakt?

Materialen

• Papier, karton of karton.
• Regel en ploeg
• Grafietpotlood en gekleurde markeringen
• Schaar
• Lijm voor ambachten.

Procedure

1. Breng de onderstaande sjabloon over, op de gewenste schaal, op karton of karton, met behulp van grafietpotlood, regel en squadron. Een andere optie is om de figuur naar een documenttype of bewerkbare tekening te kopiëren en te vergroten totdat u de gewenste afmetingen hebt.
2. Zodra de sjabloon naar papier of karton is verplaatst, moet deze met grote zorg worden gesneden.
3. Buig nu bij de stippellijnen om de piramide vorm te geven en zorg ervoor dat de zijkanten correct passen.
4. Vouw ook de wimpers, controleer of ze goed passen en voeg vervolgens lijm toe, druk ze voorzichtig zodat ze op hun plaats zijn, waardoor de figuur wordt gevormd.
5. Versier de piramide met gekleurde markeringen.

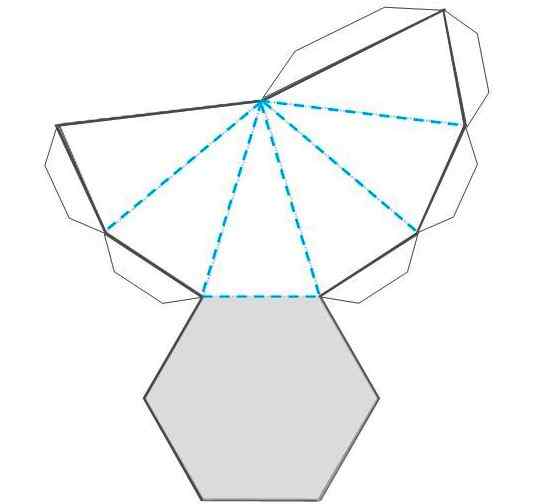figuur 3.- Sjabloon om een ​​zeshoekige piramide te knippen en te monteren. Bron: f. Zapata.

Voorbeelden van zeshoekige piramides

Volgens de basis zeshoek kunnen zeshoekige piramides zijn:

Kan u van dienst zijn: Algebraïsche taal: concept, waarvoor is het voor, voorbeelden, oefeningen

-Convex, Als alle interne hoeken van de zeshoek minder zijn dan 180º.

-Concaaf, Als een of meer van de interne hoeken van de zeshoek meer dan 180º meet.

De reguliere zeshoekige piramide van figuur 1 is convex, omdat alle interne hoeken van de basis minder dan 180º meet. Om precies te zijn, meet de interne hoeken van de reguliere zeshoek alle 120º.

Volgens dit varieert de vorm van de zeshoekige piramides, zoals dan getoond.

Oblicual zeshoekige piramide

In het beeld van figuur 4 wordt een schuine zeshoekige piramide waargenomen, waarvan de basis regelmatig is. Let op dat de driehoek die het gezicht op de voorgrond vormt, een driehoek is met zijn drie verschillende zijden (scalene driehoek), in tegenstelling tot de piramide in figuur 1, waarvan de gezichten gelijkbenig driehoeken zijn. Als een lijn wordt getrokken van het hoekpunt naar het midden van de zeshoek, blijkt deze te genezen ten opzichte van de verticale.

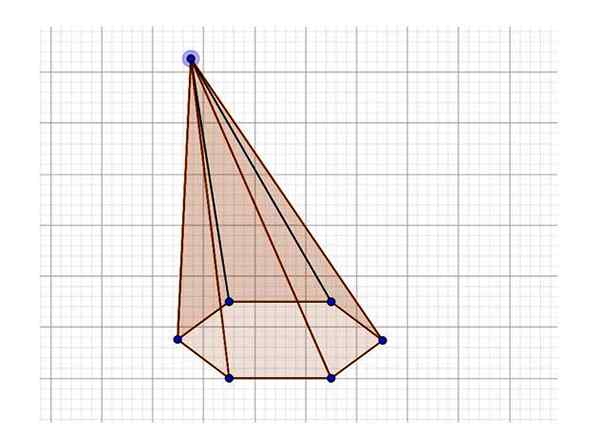Figuur 4. Voorbeeld van schuine zeshoekige piramide. Bron: f. Zapata door Geogebra.

Concava en schuine zeshoekige piramide

De basis van deze zeshoekige piramide bevat een interne hoek waarvan de maatregel groter is dan 180º, daarom is het een concave piramide, naast schuine zijn.

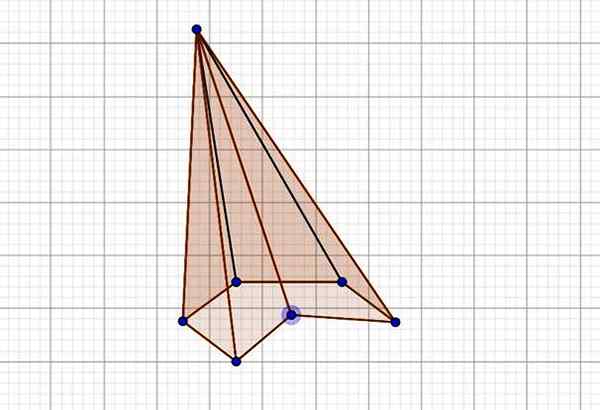Figuur 5. Schuine en concave zeshoekige piramide. Bron: f. Zapata door Geogebra.