Y = 3Sen (4x) functieperiode

Hij Y = 3Sen (4x) functieperiode Het is 2π/4 = π/2. Om de reden voor deze verklaring duidelijk te begrijpen, moet de definitie van een periode van een functie en de periode van de Sen (X) -functie bekend zijn; Een beetje over functiesgrafiek zal ook nuttig zijn.

Trigonometrische functies, zoals sinus en cosinus (sen (x) en cos (x)), zijn zeer nuttig zowel in wiskunde als engineering.

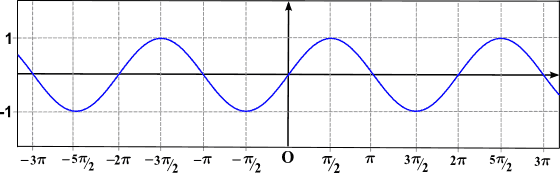
De woordperiode vermeldt de herhaling van een gebeurtenis, om te zeggen dat een functie periodiek is, is gelijk aan te zeggen: "De grafiek is de herhaling van een stuk curve". Zoals te zien is in de vorige afbeelding, is de Sen (X) -functie periodiek.

Periodieke functies

Er wordt gezegd dat een functie f (x) periodiek is als er een reële waarde p ≠ 0 is zodat f (x+p) = f (x) voor alle x in het domein van de functie. In dit geval is de periode van de functie P.

Het wordt over het algemeen een periode van de functie genoemd bij het laagste positieve reële getal P dat voldoet aan de definitie.

Zoals te zien is in de vorige grafiek, is de Sen (X) -functie periodiek en is de periode ervan 2π (de cosinusfunctie is ook periodiek, met een periode gelijk aan 2π).

Wijzigingen in de grafiek van een functie

Laat f (x) een functie zijn waarvan de grafiek bekend is, en zijn een positieve constante. Wat gebeurt er met de grafiek van f (x) als ze f (x) vermenigvuldigen met c? Met andere woorden, hoe is de grafiek van c*f (x) en f (cx)?

C*f grafiek (x)

Door een functie te vermenigvuldigen, extern, met een positieve constante, ondergaat de grafiek van F (x) een verandering in de uitgangswaarden; Dat wil zeggen, de verandering is verticaal en twee gevallen kunnen worden genomen:

- Als c> 1, lijdt de grafiek een verticale rek met een C -factor.

- JA 0

F Graph (cx)

Wanneer het argument van een functie wordt vermenigvuldigd met een constante, lijdt de grafiek van F (x) een verandering in de invoerwaarden; Dat wil zeggen, de verandering is horizontaal en, zoals voorheen, kunnen twee gevallen worden genomen:

- Als c> 1, lijdt de grafiek een horizontale compressie met een factor 1/c.

- JA 0

Y = 3Sen (4x) functieperiode

Opgemerkt moet worden dat in de functie f (x) = 3SE (4x) er twee constanten zijn die de grafiek van de sinusfunctie veranderen: de ene vermenigvuldiging van externe en een andere op een interne manier.

De 3 die zich buiten de sinusfunctie bevindt, is om de functie verticaal uit te breiden met een factor 3. Dit houdt in dat de 3SEN-functiegrafiek (x) tussen de waarden -3 en 3 zal zijn.

De 4 die zich binnen de sinusfunctie bevindt, maakt de functie -grafiek een horizontale compressie voor een 1/4 factor.

Aan de andere kant wordt de periode van een functie horizontaal gemeten. Aangezien de periode van de Sen (X) -functie 2π is, zal bij het overwegen van Sin (4x) de grootte van de periode veranderen.

Om te weten wat de periode van y = 3Sen (4x) is, vermenigvuldigt u de periode van de Sen (x) -functie met 1/4 (de compressiefactor).

Met andere woorden, de periode van de functie Y = 3Sen (4x) is 2π/4 = π/2, zoals te zien is in de laatste afbeeldingen.