Orthoeidro -formules, gebied, volume, diagonaal, voorbeelden

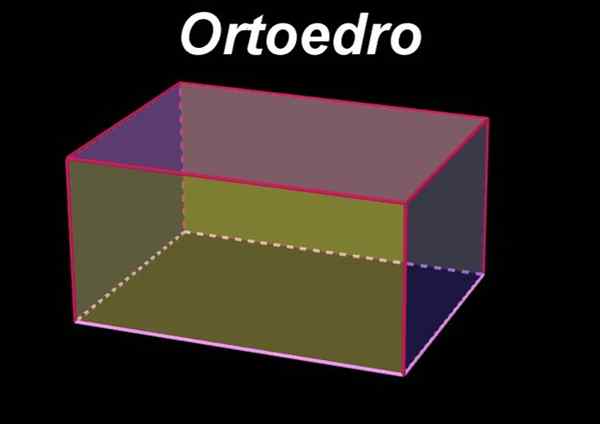
Hij Ortoedro Het is een volumetrische of drie -dimensionale geometrische figuur die wordt gekenmerkt door zes rechthoekige gezichten te hebben, zodat tegengestelde gezichten in parallelle vlakken zijn en identieke of congruente rechthoeken met elkaar zijn. Aan de andere kant staan ​​de gezichten naast een bepaald gezicht in vlakken loodrecht op die van het eerste gezicht.

Het kan ook worden overwogen wanneer Ortoedro als een orthogonaal rechthoekig basisprisma, waarin dihedros hoeken Gevormd door de twee -zijdige plannen naast een gemeenschappelijke rand, meten ze 90º. De dihedrale hoek tussen twee gezichten wordt gemeten op het snijvlak van gezichten met een loodrecht en gemeenschappelijk vlak.

Figuur 1. Ortoedro. Bron: f. Zapata met Geogebra.

Evenzo is de orthoedro een rechthoek parallelpiped, Omdat dit wordt gedefinieerd met de parallellepiped als de volumetrische figuur van zes gezichten, die parallel zijn twee tot twee.

In elke parallellepiped zijn de gezichten parallellogrammen, maar in de rechthoek parallellepiped moeten de gezichten rechthoekig zijn.

[TOC]

Delen van de orthoedro

De delen van een polyhedron, zoals de orthoedro, Zijn:

-Randen

-Hoekpunten 

-Gezichten

De hoek tussen twee randen van een gezicht van de orthoedro valt samen met de dihedrale hoek gevormd door de andere twee gezichten naast elk van de randen, waardoor de rechterkant wordt gevormd. De volgende afbeelding verduidelijkt elk concept:

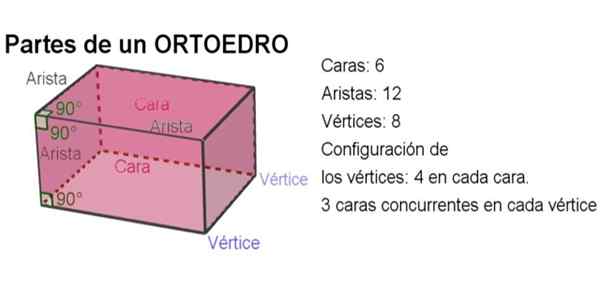Figuur 2. Delen van een orthoedro. Bron: f. Zapata met Geogebra.

-In totaal heeft een orthoentro 6 gezichten, 12 randen en 8 hoekpunten.

-De hoek tussen twee randen is een rechte hoek.

-De dihedrale hoek tussen twee zijden is ook recht.

-In elk gezicht zijn er vier hoekpunten en in elk hoekpunt aanwezig.

Kan u van dienst zijn: wat is een capicúa -nummer? Eigenschappen en voorbeelden

Orthoedro -formules

Gebied

Het oppervlak of het oppervlak van een Ortoedro Het is de som van de delen van hun gezichten.

Als de drie randen die in een hoekpunt in een hoekpunt overeenkomen maatregelen A, B en C hebben, zoals weergegeven in figuur 3, dan heeft de voorkant een gebied C⋅B En het achtergrondgezicht heeft ook een C⋅B -gebied.

Dan hebben de twee laterale gezichten een gebied A⋅b elk. En ten slotte hebben de gezichten van de vloer en het dak gebied A⋅c elk.

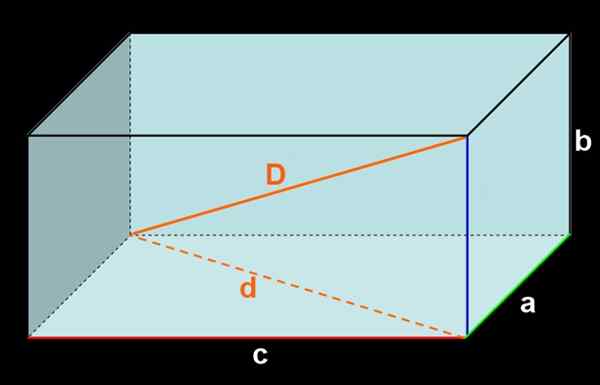figuur 3. Orthoedro van dimensies A, B, C. Interne diagonale D en externe diagonale D.

Het toevoegen van het gebied van alle gezichten wordt verkregen:

A = 2⋅C⋅B + 2⋅A⋅B + 2⋅A

Gemeenschappelijke factor trekken en de voorwaarden bestellen:

A = 2⋅ (a⋅b + b⋅c + c⋅a)

Volume

Als orthoedro als een prisma wordt beschouwd, wordt het volume als volgt berekend:

Volume = prismabase gebied x de hoogte van het prisma

In dit geval wordt de afmetingsvloer als rechthoekig genomen C En naar, Dus het basisgebied is C⋅A.

De hoogte wordt gegeven door de lengte B Van de orthogonale randen tot de zijkanten naar En C.

Het basisgebied vermenigvuldigen (A⋅c) op hoogte B Je hebt het volume V Van de orthoedro:

V = a⋅b⋅c

Interne diagonaal

In een orthoedro zijn er twee soorten diagonalen: externe diagonalen en interne diagonalen.

De externe diagonalen zijn op rechthoekige gezichten, terwijl de interne diagonalen de segmenten zijn die samenvoegen.

In een orthoedro zijn er vier interne diagonalen, allemaal van gelijke maatregelen. De lengte van de interne diagonalen kan worden verkregen bij het toepassen van de Pythagoras -stelling voor rechthoeken.

Het kan u van dienst zijn: Trigonometrische functies: Basic, in het Cartesiaanse vlak, voorbeelden, oefening

De lengte D van de externe diagonaal van de orthoedrovloer vervult de Pythagorese relatie:

D² = A² + C²

Evenzo, de interieurmetingsdiagonaal van de Pythagorische relatie:

D² = D² + B².

Het combineren van de twee eerdere uitdrukkingen die je hebt:

D² = A² + C² + B².

Ten slotte wordt de lengte van een van de interne diagonalen van de orthoedro gegeven door de volgende formule:

D = √ (a² + B² + C² )). 

Voorbeelden

- voorbeeld 1

Een metselaar bouwt een orthoedro -vormige tank waarvan de interne afmetingen zijn: 6 m x 4 m basis en 2 m hoog. Het wordt gevraagd:

a) Bepaal het binnenoppervlak van de tank als deze volledig open is in het bovenste deel. 

b) Bereken het volume van de binnenruimte van de tank.

c) Vind de lengte van een binnendiagonaal.

d) Wat is de capaciteit van de tank in liters?

Oplossing voor

We nemen de afmetingen van de rechthoekige basis a = 4 m en c = 6 m en de hoogte als b = 2 m

Het gebied van een orthoedro met de gegeven dimensies wordt gegeven door de volgende relatie:

A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)

Het is te zeggen:

A = 2⋅ (8 m² + 12 m² + 24 m²) = 2⋅ (44 m²) = 88 m²

Het vorige resultaat is het gebied van de orthoedro gesloten met de gegeven afmetingen, maar omdat het een tank is die volledig in het bovenste gedeelte is ontdekt, om het oppervlak van de binnenwanden van de tank te verkrijgen, het gebied van het ontbrekende deksel dat is:

C⋅a = 6 m ⋅ 4 m = 24 m².

Ten slotte zal het binnenoppervlak van de tank zijn: S = 88 m² - 24 m² = 64 m².

Oplossing B

Het interieurvolume van de tank wordt gegeven door het volume van een orthoedro van de binnenafmetingen van de tank:

V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m³.

Oplossing C

De binnendiagonaal van een octaëder met de afmetingen van het interieur van de tank heeft een lengte gegeven door:

Kan u van dienst zijn: continue willekeurige variabele

√ (a² + B² + C² ) = √ ((4 m)² + (2 m)² + (6 m)² ))

Het uitvoeren van de aangegeven bewerkingen die we hebben:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) m = 7,48 m.

Oplossing D

Om de tankcapaciteit in liters te berekenen, is het noodzakelijk om te weten dat het volume van een kubieke decimeter gelijk is aan de capaciteit van een liter. Het was eerder in volume berekend in kubieke meter, maar het moet worden omgezet in kubieke decimeters en vervolgens in liters:

V = 48 m³ = 48 (10 dm)³ = 4.800 dm³ = 4.800 l

- Oefening 2

Een glazen aquarium heeft een kubieke vorm van 25 cm zijde. Bepaal het gebied in m², Het volume in liters en de lengte van een interieur diagonaal in CM.

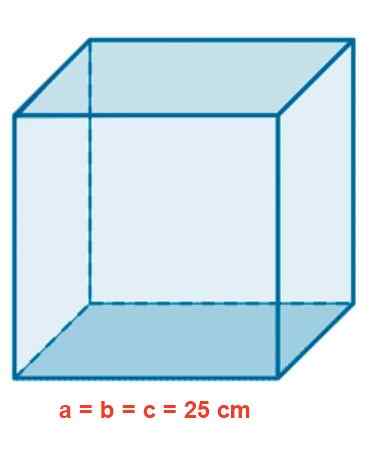Figuur 4. Kubisch glazen aquarium.

Oplossing

Het gebied wordt berekend door dezelfde orthoedro -formule, maar rekening houdend met dat alle dimensies identiek zijn:

A = 2⋅ (3 a⋅a) = 6⋅ a² = 6⋅ (25 cm)² = 1.250 cm²

Het volume van de kubus wordt gegeven door:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 dm)³ = 15,625 DM³ = 15,625 l.

De lengte D van de binnendiagonaal is:

D = √ (3e²) = 25√ (3) cm = 43,30 cm.

Referenties

1. Arias J. Geogebra: Prism. Hersteld van: YouTube.com.
2. Berekening.DC. Oefeningen en problemen opgelost in gebieden en volumes. Teruggewonnen uit: berekening.DC.
3. Salvador r. Pyramid + orthoedro met Geogebra (IHM). Hersteld van: YouTube.com
4. Weisstein, Eric. "Ortoedro". Wiskunde. Wolfram -onderzoek.
5. Wikipedia. Ortoedro. Hersteld van: is.Wikipedia.com