Transcendente getallen die, formules, voorbeelden, oefeningen zijn

De transcendente cijfers Het zijn die die niet kunnen worden verkregen als gevolg van een polynoomvergelijking. Het tegenovergestelde van een transcendent nummer is een algebraïsch nummer, die oplossingen zijn van een polynoomvergelijking van het type:

naar_N X^N + naar_N-1 X^N-1 +… + A₂ X² + naar₁ x + a₀ = 0

Waar de coëfficiënten_N, naar_N-1,… naar₂, naar₁, naar₀ Het zijn rationele getallen, genoemd polynoomcoëfficiënten. Als een X -nummer een oplossing is van de vorige vergelijking, is dat nummer niet transcendent.

Figuur 1. Twee aantallen groot belang in de wetenschap zijn transcendente cijfers. Bron: Public DomainPartures.netto.

We zullen een paar nummers analyseren en kijken of ze al dan niet transcendent zijn:

a) 3 is niet transcendent omdat het een oplossing is van x - 3 = 0.

b) -2 kan niet transcendent zijn omdat het een oplossing is van x + 2 = 0.

c) ⅓ Het is 3x - 1 = 0 oplossing

d) Een oplossing van vergelijking x² - 2x + 1 = 0 is √2 -1, dus het nummer per definitie is niet transcendent.

e) noch is √2 omdat het het resultaat is van vergelijking x² - 2 = 0. Door √2 vierkant te verhogen, resulteert het in 2, die van 2 worden afgetrokken, maakt niet uit tot nul. Dus √2 is een irrationeel getal, maar het is niet transcendent.

[TOC]

Wat zijn transcendente cijfers?

Het probleem is dat er geen algemene regel is om ze te verkrijgen (later zullen we een vorm zeggen), maar enkele van de beroemdste zijn het nummer pi en de NEPER -nummer, respectievelijk aangeduid door: π En En.

Het nummer π

Het nummer π Lijkt natuurlijk dat het wiskundige quotiënt tussen de perimeter P van een cirkel en de diameter D D, ongeacht of het een kleine of grote cirkel is, altijd hetzelfde nummer geeft, genaamd pi:

π = P/D ≈ 3.14159…

Dit betekent dat als de diameter van de omtrek wordt genomen als een meeteenheid, voor alle, of ze nu groot of klein zijn, de perimeter altijd waard zal zijn p = 3.14 ... = π, Zoals te zien is in de animatie van figuur 2.

Kan u van dienst zijn: Bolzano Stelling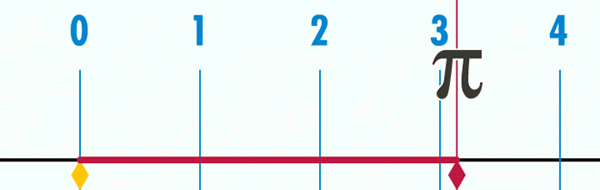Figuur 2. De omtreklengte van een cirkel is soms de lengte van de diameter, die ongeveer 3.1416 is.

Om meer decimalen te bepalen, moet u meer precisie P en D meten en vervolgens het quotiënt berekenen, dat op de wiskundige manier is gedaan. De conclusie is dat de decimalen van het quotiënt geen einde hebben en nooit worden herhaald, dus het nummer π Naast transcendent zijn het ook irrationeel.

Een irrationeel nummer is dat nummer dat niet kan worden uitgedrukt als de verdeling van twee hele getallen. 

Het is bekend dat elk transcendent getal irrationeel is, maar het is niet waar dat alle irrationele transcendent zijn. √2 is bijvoorbeeld irrationeel, maar het is niet transcendent.

figuur 3. Transcendente cijfers zijn irrationeel, maar de wederzijdse verklaring is niet waar.

Het nummer e

Het transcendente nummer is de basis van de Neperiaanse logaritmen en hun decimale benadering is:

E ≈ 2.718281828459045235360… .

Als u het nummer wilde schrijven En Precies, het zou nodig zijn om decimaal oneindig te schrijven, omdat elk transcendent aantal irrationeel is, zoals eerder gezegd.

De eerste tien cijfers van En Ze zijn gemakkelijk te onthouden:

2.7 1828 1828 En hoewel het een repetitief patroon lijkt te volgen, wordt dit niet bereikt in de decimalen van orde groter dan negen.

Een meer formele definitie van En is de volgende:

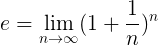
Wat betekent dat de exacte waarde van En De in deze formule aangegeven bewerking wordt bereikt wanneer het natuurlijke nummer N Het heeft de neiging om oneindig te zijn.

Dit verklaart waarom we alleen benaderingen kunnen verkrijgen En, Omdat hoe groot het nummer n is geplaatst, kunt u altijd een N bejaard.

Laten we zelf naar een aantal benaderingen zoeken:

-Wanneer n = 100 dan (1 + 1/100)¹⁰⁰ = 2.70481 die nauwelijks samenvalt in het eerste decimaal met de "echte" waarde van E.

-Als u wordt gekozen n = 10.000 die je hebt (1 + 1/10.000)^10.000 = 2.71815 die samenvalt met de "exacte" waarde van E in de eerste drie decimalen.

Kan u van dienst zijn: homologe kanten

Dit proces moet worden gevolgd om de "echte" waarde van E te kunnen verkrijgen. Ik denk niet dat we tijd hebben om het te bereiken, maar laten we nog een poging doen:

Laten we n = 100 gebruiken.000:

(1 + 1/100.000)^100.000 = 2.7182682372

Dat er slechts vier decimalen samenvallen met de waarde die als nauwkeurig wordt beschouwd.

Het belangrijkste is om te begrijpen dat hoe groter de waarde van N is gekozen om te berekenen en_N, dichterbij zal van de werkelijke waarde zijn. Maar die werkelijke waarde zal alleen worden gehouden als N oneindig is.

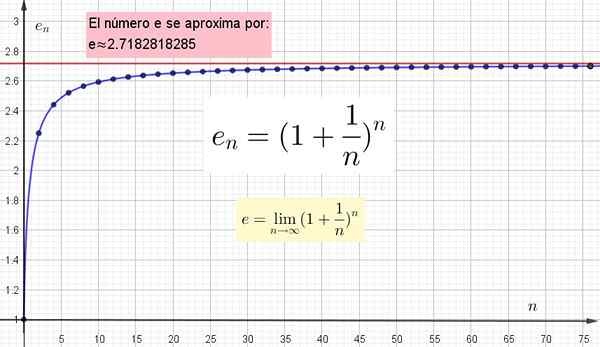Figuur 4. Het wordt grafisch weergegeven als de hogere waarde van N dichter bij E is, maar om de exacte waarde te bereiken N moet oneindig zijn.

Andere transcendente cijfers

Afgezien van deze beroemde nummers zijn er bijvoorbeeld andere transcendente nummers:

- 2^√2

Elk algebraïsch nummer, dat niet 0 of 1 is, verhoogd tot een irrationele exponent zal een transcendent nummer zijn.

-Champernowne's nummer 10: 

C_10 = 0.123456789101112131415161718192021… .

-Champernowne's nummer op basis 2:

C_2 = 0.110111001011011… .

-Het γ of constante gamma-aantal Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

Dat wordt verkregen door de volgende berekening te doen:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1/n - ln (n)

Wanneer N Wees erg groot. Om de exacte waarde van het gamma -nummer te hebben, zou het nodig zijn om mee te berekenen N oneindig. Iets vergelijkbaar met wat we hierboven hebben gedaan.

En er zijn nog veel meer transcendente cijfers. De grote wiskundige Georg Cantor, geboren in Rusland en leefde tussen 1845 en 1918, toonde aan dat de reeks transcendente nummers veel groter is dan de set algebraïsche getallen.

Formules waarbij het transcendente nummer π verschijnt

De omtrek van de omtrek

P = π d = 2 π r, waarbij p de perimeter is, d de diameter en r de straal van de omtrek. Er moet aan worden herinnerd dat:

Kan u van dienst zijn: hoeveel moet u toevoegen aan 3/4 om 6/7 te krijgen?

-De diameter van de omtrek is het langste segment dat twee punten ervan verbindt en dat altijd door het midden gaat,

-De straal is de helft van de diameter en is het segment dat van het midden naar de rand gaat.

Cirkelgebied

A = π r² = ¼ π d²

Oppervlak van een bol

S = 4 π r^2.

Ja. Hoewel het niet lijkt, is het oppervlak van een bol hetzelfde als dat van vier cirkels van dezelfde straal als de bol.

Bolvolume

V = 4/3 π r³

Opdrachten

- Oefening 1

De "exotische" pizzeria verkoopt pizza's met drie diameter: 30 cm klein, mediane 37 cm en grote 45 cm. Een kind is erg hongerig en realiseerde zich dat twee kleine pizza's dezelfde kosten hebben als een grote. Wat zal beter voor hem zijn, twee kleine pizza's of een grote kopen?

Figuur 5.- Het gebied van een pizza is evenredig met het kwadraat van de straal, is de evenredigheidsconstante. Bron: Pixabay.

Oplossing

Hoe groter het gebied, hoe groter de hoeveelheid pizza, om deze reden zal het gebied van een grote pizza worden berekend en vergeleken met dat van twee kleine pizza's:

Groot pizzabeeld = ¼ π d² = ¼ ⋅3,1416⋅45² = 1590,44 cm²

Klein pizzabeeld = ¼ π d² = ¼ ⋅3,1416⋅30² = 706,86 cm²

Daarom zullen twee kleine pizza's een gebied hebben 

2 x 706.86 = 1413.72 cm² .

Het is duidelijk: er zal meer pizza zijn die een enkele grote dan twee kleintjes koopt.

- Oefening 2

De "exotische" pizzeria verkoopt ook een straal van 30 cm straal semi -man -pizza voor dezelfde rechthoekige vorm van 30 x 40 cm zijde. Welke zou jij kiezen?

Figuur 6.- Het oppervlak van een semi -sprezer is twee keer het cirkelvormige oppervlak van de basis. Bron: f. Zapata.

Oplossing

Zoals vermeld in de vorige sectie, is het oppervlak van een bol vier keer groter dan dat van een cirkel met dezelfde diameter, dus een semi -speer van 30 cm zal hebben:

30 cm semi -man -pizza: 1413.72 cm² (tweemaal een cirkelvormige met dezelfde diameter)

Rechthoekige pizza: (30 cm) x (40 cm) = 1200 cm² .

Semi -man -pizza heeft een groter gebied.

Referenties

1. Fernández J. Het nummer e. Oorsprong en curiosa. Hersteld van: Soja Mathematics.com
2. Geniet van wiskunde. Euler's nummer. Hersteld van: geniet van Matimaticas.com.
3. Figuera, j. 20000000000000000000. Wiskunde 1e. Diversifieerd. Co-bo edities.
4. Garcia, m. Het nummer e in de elementaire berekening. Hersteld van: wiskunde.Ciens.UCV.gaan.
5. Wikipedia. PI -nummer. Hersteld van: Wikipedia.com
6. Wikipedia. Transcendente cijfers. Hersteld van: Wikipedia.com