Irrationele getallen geschiedenis, eigenschappen, classificatie, voorbeelden

De irrationele nummers Zij zijn degenen wiens decimale expressie oneindige figuren heeft zonder een repetitief patroon, daarom kunnen ze niet worden verkregen door het quotiënt tussen twee gehele getallen te maken.

Een van de bekendste irrationele cijfers zijn:

Figuur 1. Van boven naar beneden de volgende irrationele getallen: PI, het aantal Euler, de Aúrea en twee vierkante wortels. Bron: Pixabay.

Onder hen is zonder twijfel π (pi) het meest bekend, maar er zijn er nog veel meer. Ze behoren allemaal tot de reeks reële getallen, wat de numerieke set is die rationele en irrationele cijfers samenbrengt.

De suspensieve punten in figuur 1 geven aan dat de decimalen voor onbepaalde tijd volgen, wat er gebeurt, is dat de ruimte van de huidige rekenmachines er slechts enkele toestaat om er een paar te laten zien.

Als we zorgvuldig kijken, op voorwaarde dat we het quotiënt tussen twee gehele getallen maken, wordt een decimaal met beperkte cijfers verkregen of zo niet, met oneindige figuren waarin ze worden herhaald. Nou, dit gebeurt niet met irrationele cijfers.

[TOC]

Geschiedenis van irrationele cijfers

De grote wiskundige van de oudheid Pythagoras, geboren in 582 tot.C in Samos, Griekenland, stichtte de Pythagorische school van gedachten en ontdekte de beroemde stelling die zijn naam draagt. We hebben het links (de Babyloniërs konden hem al lang eerder kennen).

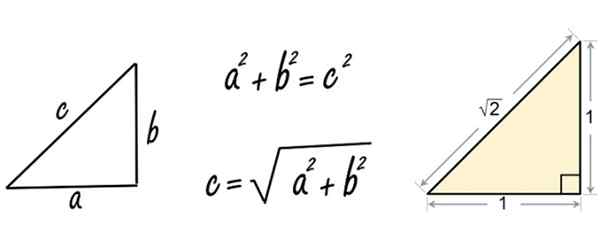Figuur 2. Pythagoras stelling toegepast op een driehoek van zijkanten gelijk aan 1. Bron: Pixabay/Wikimedia Commons.

Welnu, toen Pythagoras (of waarschijnlijk een discipel van hem) de stelling toepaste op een rechter driehoek van zijden gelijk aan 1, vond het irrationele getal √2.

Het kan u van dienst zijn: droge lijnen

Hij deed het op deze manier:

C = √1² + 1² = √1+1 = √2

En hij realiseerde zich onmiddellijk dat dit nieuwe nummer niet voortkwam uit het quotiënt tussen twee andere natuurlijke getallen, die die op dat moment waren die bekend waren.

Daarom belde hij hem irrationeel, En de ontdekking veroorzaakte grote angst en verwarring onder de Pythagoreeërs.

Eigenschappen van irrationele getallen

-De set van alle irrationele getallen wordt aangegeven met de letter I en soms zoals Q* of Q^C. De unie tussen irrationele getallen I of Q* en rationele getallen q, geeft aanleiding tot de reeks reële ncijfers.

-Met irrationele getallen kunnen bekende rekenkundige bewerkingen worden uitgevoerd: som, aftrekking, vermenigvuldiging, verdeling, potentiëring en meer.

-De verdeling tussen 0 is niet gedefinieerd tussen irrationele cijfers.

-De som en het product tussen irrationele getallen is niet noodzakelijkerwijs een ander irrationeel aantal. Bijvoorbeeld:

√2 x √8 = √16 = 4

En 4 is geen irrationeel aantal.

-De som van een rationeel getal plus een irrationele resultaat leidt echter tot een irrationele. Op deze manier:

1 + √2 = 2.41421356237…

-Het product van een ander rationeel getal dan 0 door een irrationeel nummer is ook irrationeel. Laten we naar dit voorbeeld kijken:

2 x √2 = 2.828427125…

-Het omgekeerde van een irrationeel resultaat in een ander irrationeel aantal. Laten we wat proberen:

1 / √2 = 0.707106781…

1 / √3 = 0.577350269…

Deze cijfers zijn interessant omdat ze ook de waarden zijn van enkele trigonometrische redenen voor bekende hoeken. Veel van de trigonometrische redenen zijn irrationele cijfers, maar er zijn uitzonderingen, zoals Sen 30º = 0.5 = ½, wat rationeel is.

-In de som worden aan de commutatieve en associatieve eigenschappen bereikt. Als A en B twee irrationele getallen zijn, betekent dit dat:

Kan u van dienst zijn: overjectieffunctie: definitie, eigenschappen, voorbeelden

A + B = B + A.

En als C een ander irrationeel nummer is, dan:

(A + b) + c = a + (b + c).

-De distributieve eigenschap van vermenigvuldiging met betrekking tot de som is een andere bekende eigenschap die ook wordt voldaan voor irrationele getallen. In dit geval:

naar.(b+c) = a.B + A.C.

-Een irrationeel om zijn tegenovergestelde te hebben: -a. Wanneer het resultaat is toegevoegd, is het 0:

A+(-a) = 0

-Tussen twee verschillende rationele.

Locatie van een irrationeel nummer op de echte lijn

De echte lijn is een horizontale lijn waar de reële getallen zich bevinden, waarvan de irrationele een belangrijk onderdeel is.

Om een ​​irrationeel nummer op de echte lijn te vinden, in een geometrische vorm, kunnen we de Pythagoras -stelling, een regel en een kompas waard zijn.

Als voorbeeld gaan we √5 op de echte lijn vinden, waarvoor we een rechthoekige driehoek van kanten trekken x = 2 En y = 1, Zoals de foto laat zien:

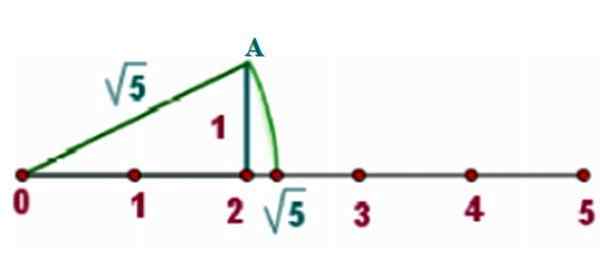figuur 3. Methode voor het vinden van een irrationeel nummer op de echte lijn. Bron: f. Zapata.

Voor de stelling van Pythagoras is de hypotenusa van een dergelijke driehoek:

C = √2² + 1² = √4+1 = √5

Nu is de beat met de punt in 0 geplaatst, waar ook een van de hoekpunten van de juiste driehoek is. De punt van het kompaspotlood moet bij het hoekpunt zijn.

Er wordt een omtrekboog getekend die de echte lijn snijdt. Aangezien de afstand tussen het midden van de omtrek en elk punt van hetzelfde de straal is, die waard is √5, is het snijpunt ook √5 uit het midden.

Van de grafiek is te zien dat √5 tussen 2 en 2 is.5. Een rekenmachine biedt ons de geschatte waarde van:

Kan u van dienst zijn: Bepalingscoëfficiënt: formules, berekening, interpretatie, voorbeelden

√5 = 2.236068

En dus, het bouwen van een driehoek met de juiste kanten, andere irrationele kan worden gevonden, zoals √7 en andere.

Classificatie van irrationele cijfers

Irrationele cijfers zijn ingedeeld in twee groepen:

-Algebraïsch

-Transcendent of transcendentaal

Algebraïsche nummers

Algebraïsche getallen, die irrationeel kunnen zijn of niet, zijn oplossingen van polynoomvergelijkingen waarvan de algemene vorm is:

naar_N X^N + naar_N-1X^N-1 + naar_N-2X^N-2 +.. . +naar₁x + a_of = 0

Een voorbeeld van polynoomvergelijking is een tweede graad vergelijking als deze:

X³ - 2x = 0

Het is gemakkelijk om aan te tonen dat het irrationele nummer √2 een van de oplossingen van deze vergelijking is.

Transcendente cijfers

In plaats daarvan ontstaan ​​transcendente cijfers, hoewel irrationeel, nooit als een oplossing van een polynoomvergelijking.

De transcendente getallen die het meest worden gevonden in de toegepaste wiskunde zijn π, voor hun relatie met de omtrek en nummer E, of Euler -nummer, wat de basis is van de Neperian Logaritms.

Oefening

Op een zwart vierkant wordt een grijs geplaatst in de positie aangegeven in de figuur. Het is bekend dat het oppervlak van het zwarte vierkant 64 cm is². Hoeveel zijn de lengte van beide vierkanten?

Figuur 4. Twee vierkanten, waarvan de lengte van de zijkanten te vinden is. Bron: f. Zapata.

Antwoord

Het oppervlak van een vierkant van zij L is:

A = L²

Omdat het zwarte vierkant 64 cm is² van gebied, de zijde moet 8 cm zijn.

Deze maat is hetzelfde als De diagonaal van het grijze vierkant. Het toepassen van de Pythagoras -stelling op deze diagonaal, en onthouden dat de zijkanten van een vierkante meten hetzelfde zullen hebben, zullen we hebben:

8² = L_G² + L_G²

Waar l_G Het is de zijkant van het grijze vierkant.

Daarom: 2l_G² = 8²

Vierkante wortel toepassen aan beide zijden van gelijkheid:

L_G = (8/√2) cm

Referenties

1. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding. Nationale Universiteit van de kust.
2. Figuera, j. 20000000000000000000. Wiskunde 9e. Rang. Co-bo edities.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Onderwijsportaal. Irrationele cijfers en hun eigenschappen. Opgehaald uit: portaleducatief.netto.
5. Wikipedia. Irrationele nummers. Hersteld van: is.Wikipedia.borg.