Complementaire hoeken welke en hoe worden berekend, voorbeelden, oefeningen

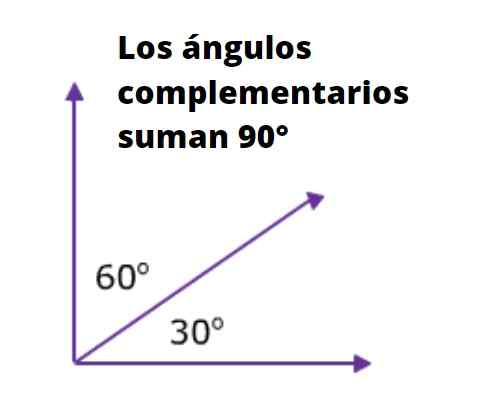
Twee of meer hoeken zijn Complementaire hoeken Als de som van de maatregelen overeenkomt met die van een rechte hoek. Zoals bekend is de maat van een rechthoek in graden 90º, en in radianen is het π/2.

De twee hoeken naast de hypotenusa van een rechthoekige driehoek zijn bijvoorbeeld complementair aan elkaar, omdat de som van hun maatregelen 90º is. De volgende figuur is er erg illustratief over:

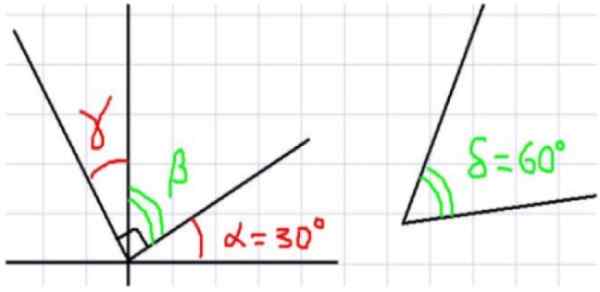Figuur 1. Links, verschillende hoeken met een gemeenschappelijk hoekpunt. Rechts een hoek van 60º die een aanvulling vormt op de hoek α (alfa). Bron: f. Zapata.

Figuur 1 toont in totaal vier hoeken. α en β zijn complementair omdat ze dat zijn aangrenzend en het is een volledige som een ​​rechte hoek. Evenzo is β complementair aan γ, waar volgt dat γ en α van gelijke mate zijn.

Nu, omdat de som van α en δ gelijk is aan 90 graden, kan worden gezegd dat α en δ complementair zijn. Bovendien, aangezien β en δ dezelfde complementaire α hebben, kan worden gezegd dat β en δ dezelfde maat hebben.

 [TOC]

Voorbeelden van complementaire hoeken

In de volgende voorbeelden wordt gevraagd om de onbekende hoeken te vinden, aangegeven met ondervraging in figuur 2.

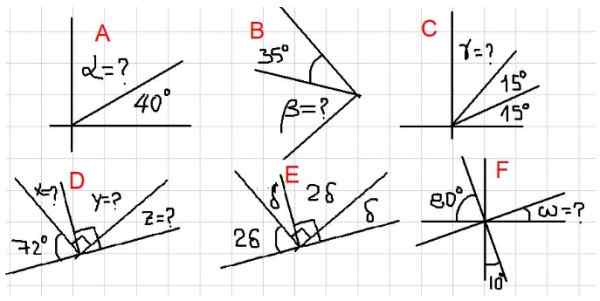Figuur 2. Verschillende voorbeelden van complementaire hoeken. Bron: f. Zapata.

- Voorbeelden A, B en C

De volgende voorbeelden zijn in volgorde van complexiteit.

Voorbeeld a

In de bovenste figuur hebben we dat de aangrenzende hoeken α en 40º een rechte hoek oplossen. Dat is α + 40º = 90º, daarom α = 90º- 40º = 50º.

Voorbeeld B

Aangezien β complementair is met de hoek van 35º, dan β = 90º - 35º = 55º.

Kan u van dienst zijn: orthoedro: formules, gebied, volume, diagonaal, voorbeelden

Voorbeeld c

Uit figuur 2c, de som van γ + 15º + 15º = 90º = 90º. Dat wil zeggen dat γ complementair is in hoek 30 = 15º + 15º. Zodat:

γ = 90º- 30º = 60º

- Voorbeelden D, E en F

In deze voorbeelden zijn er meer hoeken bij betrokken. Om de onbekenden te vinden, moet de lezer het concept van complementaire hoek zo vaak als nodig toepassen.

Voorbeeld D

Omdat x complementair is met 72º, volgt hieruit dat x = 90º - 72º = 18º = 18º. Bovendien is het complementair met x, dan y = 90º - 18º = 72º.

Eindelijk is Z complementair aan en. Uit al het bovenstaande volgt dat:

Z = 90º - 72º = 18º

Voorbeeld e

De hoeken Δ en 2δ zijn complementair, daarom Δ + 2δ = 90º.

Dat is 3δ = 90º, wat inhoudt dat Δ = 90º / 3 = 30º.

Voorbeeld f

Als we de hoek tussen ω en die van 10 noemen, moet deze dan aan hen worden aangevuld, omdat wordt opgemerkt dat hun volledige som een ​​rechte hoek. Waar volgt dat u = 80º. Omdat U complementair is met ω, dan ω = 10º.

Opdrachten

Hieronder worden drie oefeningen voorgesteld. In allemaal moet de waarde van hoeken A en B in graden worden gevonden, zodat de relaties in figuur 3 worden voldaan.

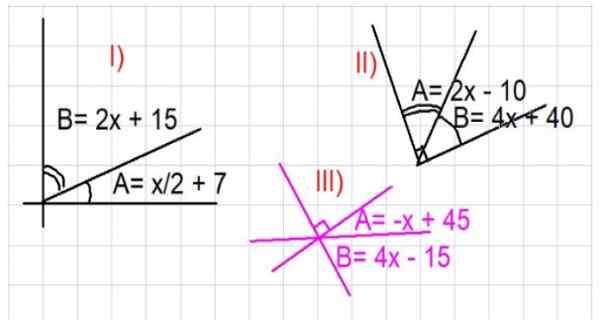figuur 3. Illustraties voor complementaire hoeken oefeningen. Bron: f. Zapata.

- Oefening 1

Bepaal de waarden van hoeken A en B van deel I) van figuur 3.

Oplossing

Uit de getoonde figuur blijkt dat A en B complementair zijn, daarom A + B = 90º. De uitdrukking van A en B wordt vervangen als een functie van X gegeven in deel I):

Kan u van dienst zijn: Convergence Radio: Definitie, voorbeelden en oefeningen opgelost

(x/2 + 7) + (2x + 15) = 90

Vervolgens zijn de termen correct gegroepeerd en wordt een eenvoudige lineaire vergelijking verkregen:

(5x/2) + 22 = 90

22 aftrekken in beide leden zijn:

5x/2 = 90 -22 = 68

En ten slotte wordt de waarde van X gewist:

x = 2*68/5 = 136/5

Nu wordt de hoek gevonden die de waarde van x vervangt:

A = (136/5)/2 +7 = 103/5 = 20,6 º.

Terwijl Angle B is:

B = 2*136/5 + 15 = 347/5º = 69,4º .

- Oefening 2

Zoek de waarden van hoeken A en B van afbeelding II, figuur 3.

Oplossing

Nogmaals, omdat A en B complementaire hoeken zijn, moet je: A + B = 90º zijn. De expressie van A en B vervangen als een functie van X gegeven in deel II) van figuur 3 is:

(2x - 10) + (4x +40) = 90

De vergelijkbare termen zijn gegroepeerd om de vergelijking te verkrijgen:

6 x + 30 = 90

Beide leden verdelen tussen 6 wordt verkregen:

x + 5 = 15

Waar volgt dat x = 10º.

Daarom:

A = 2*10 - 10 = 10º

B = 4*10 + 40 = 80º.

- Oefening 3

Bepaal de waarden van hoeken A en B van deel III) van figuur 3.

Oplossing

De figuur wordt zorgvuldig geanalyseerd om te zoeken naar complementaire hoeken. In dit geval moet u + B = 90 graden. Als u de expressie van A en B vervangt als een functie van X die in de figuur wordt gegeven, hebt u:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Beide leden verdelen door 3 is de volgende:

x + 10 = 30

Waar volgt dat x = 20º.

Dat wil zeggen dat de hoek A = -20 +45 = 25º. En van zijn deel: B = 4*20 -15 = 65º.

Loodrechte zijden hoeken

Er wordt gezegd dat twee hoeken zijn loodrechte kanten Als elke partij zijn overeenkomstige loodrecht in de andere heeft. De volgende figuur verduidelijkt het concept:

Kan u van dienst zijn: samengestelde opvolging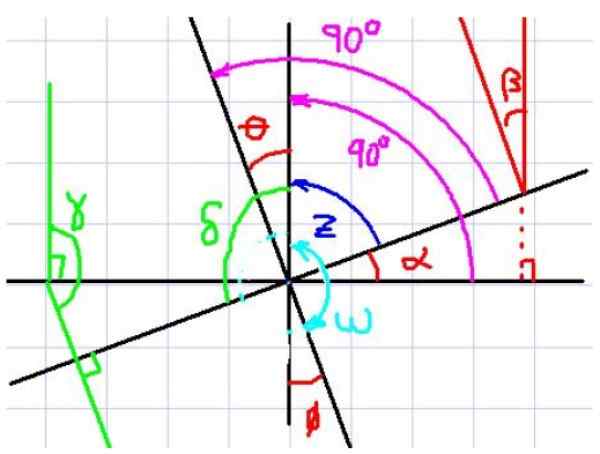Figuur 4. Loodrechte zijden hoeken. Bron: f. Zapata.

In figuur 4 worden de hoeken α en θ bijvoorbeeld waargenomen. Merk nu op dat elke hoek zijn overeenkomstige loodrecht heeft in de andere hoek.

Het wordt ook gezien dat α en θ dezelfde complementaire hoek hebben Z, Daarom concludeert de waarnemer onmiddellijk dat α en θ dezelfde maat hebben. Het lijkt dan dat als twee hoeken loodrechte kanten met elkaar hebben, ze hetzelfde zijn, maar laten we een ander geval bekijken.

Overweeg nu de hoeken α en ω. Deze twee hoeken hebben ook overeenkomstige loodrechte kanten, maar er kan niet worden gezegd dat ze van gelijke mate zijn, omdat de ene acuut is en de andere stompe is.

Merk op dat ω + θ = 180º. Behalve θ = α. Als u deze uitdrukking van Z vervangt in de eerste vergelijking, krijgt u:

δ + α = 180º, dat is dat δ en α hoeken zijn van wederzijds loodrechte zijden.

Algemene regel voor loodrechte zijden hoeken 

Uit de bovengenoemde, een regel die altijd wordt vervuld dat de hoeken loodrechte kanten hebben, kunnen worden vastgesteld:

Als twee hoeken elkaar voor elkaar loodrechte zijden zijn, zijn ze hetzelfde als beide acuut zijn of beide stompe zijn. Anders, als de ene acuut is en de andere stompe is, dan zijn ze aanvullend, dat wil zeggen, ze voegen 180º toe.

Het toepassen van deze regel en in verwijzing naar de hoeken van figuur 4 kunnen we het volgende bevestigen:

α = β = θ = φ

γ = δ

Met de ω aanvullende hoek van α, β, θ en φ.

Referenties

1. Baldor, J. NAAR. 1973. Flat and Space Geometry. Midden -Amerikaans cultureel. 
2. Wiskundige wetten en formules. Hoek meetsystemen. Opgehaald uit: ingemecanica.com.
3. Wentworth, G. Planeetgeometrie. Hersteld van: Gutenberg.borg.
4. Wikipedia. Complementaire hoeken. Hersteld van: is.Wikipedia.com
5. Wikipedia. Transportband. Hersteld van: is.Wikipedia.com
6. Zapata F. Goniometer: geschiedenis, onderdelen, operatie. Opgehaald uit: lifer.com