Centrale symmetrie -eigenschappen, voorbeelden en oefeningen

Twee punten a en 'hebben centrale symmetrie Wat betreft een punt of wanneer het AA -segment er doorheen gaat en ook het middelpunt van AA is '. Tot het punt of wordt gebeld Symmetriecentrum.

De centrale symmetrische van een ABC -driehoek ten opzichte van het ene punt of, is een andere driehoek a'b'c 'die de volgende kenmerken heeft:

-Homologe segmenten zijn gelijke lengte 

-Hun overeenkomstige hoeken hebben dezelfde maatregel.

Figuur 1. ABC Triangle en zijn symmetrische a'b'c '. Bron: f. Zapata.

In figuur 1 een ABC -driehoek (rood) en zijn centrale symmetrische a'b'c '(groen), met betrekking tot het centrum van symmetrie of. 

In dezelfde figuur zou een attente waarnemer zich realiseren dat hetzelfde resultaat wordt verkregen door een originele driehoeksrotatie toe te passen, zolang deze 180º is en gericht is op of.

Daarom is een centrale symmetrie gelijk aan een 180º -beurt ten opzichte van het symmetriecentrum.

[TOC]

Eigenschappen van centrale symmetrie

Een centrale symmetrie heeft de volgende eigenschappen:

-Het Symmetry Center is het middelpunt van het segment dat een punt met zijn symmetrische verbindt.

-Een symmetrisch punt van een ander dat zich in het symmetriecentrum bevindt, valt samen met het midden van de symmetrie.

-De centrale symmetrische van een driehoek is een congruente driehoek (gelijk) aan het origineel.

-Het beeld door centrale symmetrie van een omtrek is een andere omtrek van gelijke straal.

-Een cirkel heeft centrale symmetrie ten opzichte van zijn eigen centrum.

Figuur 2. Ontwerp met centrale symmetrie. Bron: Pixabay.

-De ellips heeft een centrale symmetrie ten opzichte van het centrum.

-Een segment heeft een centrale symmetrie ten opzichte van zijn middelpunt.

-De gelijkzijdige driehoek heeft geen centrale symmetrie ten opzichte van het midden, omdat zijn symmetrische, hoewel congruent met de eerste, een gelijkzijdige driehoek geeft.

Het kan u van dienst zijn: y = 3Sen (4x) functieperiode

-Vierkanten hebben centrale symmetrie ten opzichte van hun centrum.

-Een Pentagon mist centrale symmetrie ten opzichte van het midden.

-Regelmatige polygonen hebben centrale symmetrie wanneer ze een aantal koppelkanten hebben.

Voorbeelden

De symmetriecriteria hebben veel toepassingen in wetenschap en engineering. Centrale symmetrie is aanwezig in de natuur, bijvoorbeeld ijskristallen en spinnenwebben hebben dit soort symmetrie.

Bovendien worden veel problemen gemakkelijk opgelost wanneer het bestaan ​​van centrale symmetrie en andere soorten symmetrie wordt gebruikt. Daarom is het handig om snel te identificeren wanneer het zich voordoet.

figuur 3. IJskristallen hebben centrale symmetrie. Bron: Pixabay.

voorbeeld 1

Gegeven een punt P van coördinaten (a, b), moet u de coördinaten van zijn symmetrische p 'vinden met betrekking tot de oorsprong of coördinaten (0, 0).

Het eerste is om de P 'P' te bouwen, waarvoor een lijn wordt getrokken die door de oorsprong of en door punt P gaat. De vergelijking van deze lijn is y = (b/a) x.

Laten we nu (a ', b') de coördinaten van het symmetrische punt p noemen. Punt P. Bovendien moet de OP -afstand gelijk zijn aan OP ', die analytisch zo schrijft:

√ (a² + B²) = √ (a '² + B '² ))

Het volgende is om b '= [(b/a) te vervangen.A '] in de vorige uitdrukking en vierkant aan beide zijden van gelijkheid om de vierkantswortel te elimineren: (a² + B²) = [A '² + (B²/naar²)).naar'²]

Door de gemeenschappelijke factor en vereenvoudiging te extraheren, wordt het bereikt '² = A². Deze vergelijking heeft twee echte oplossingen: a '= +a of a' = -a. 

Om B 'te verkrijgen, gebruiken we opnieuw B' = (B/A) A '. Als de positieve oplossing van A wordt vervangen, wordt bereikt dat B '= B. En wanneer de negatieve oplossing wordt vervangen, dan B '= -b. 

Kan u van dienst zijn: wat zijn de 7 elementen van de omtrek?

De positieve oplossing geeft voor P 'hetzelfde punt P, dus het is uitgesloten. De negatieve oplossing biedt absoluut de coördinaten van het symmetrische punt:

P ': (-a, -b)

Voorbeeld 2

Het is vereist om aan te tonen dat een AB -segment en zijn symmetrische centrale a'b dezelfde lengte hebben.

Beginnend met de coördinaten van punt A, die zijn (Axe, AY) en die van punt B: (bx, door), wordt de lengte van de AB gegeven door:

D (ab) = √ ((bx - ax)² + (Door - ay)² ))

Naar analogie zal het symmetrische segment a'b 'lengte hebben gegeven door:

d (a'b ') = √ ((bx' - ax ')² + (Door ' - ay')² ))

De coördinaten van het symmetrische punt a 'zijn ax' = -AX en ay '= -ay. Evenzo zijn die van B 'bx' = -bx en door '= -By. Als deze coördinaten worden vervangen in de vergelijking van afstand D (a'b '), heb je:

D (a'b ') = √ ((-bx + ax)² + (-By + ay)²) dat is gelijk aan:

 √ ((bx - ax)² + (Door - ay)²) = D (AB)

Aangetoond worden dat beide segmenten dezelfde lengte hebben.

Opgeloste oefeningen

- Oefening 1

Demonstreer op een analytische manier dat de centrale symmetrische of een cirkel van straal R en midden of dezelfde oorspronkelijke omtrek is.

Oplossing

De vergelijking van een straal R en middencirkel (0,0) is:

X² + En² = R² (Omtrekvergelijking c)

Als op elk punt P van de omtrek en coördinaten (x, y) zijn symmetrische coördinaat p ') wordt gevonden, is de vergelijking van de symmetrische omtrek:

X '² + En'² = R² (Symmetrische omtrekvergelijking C ')

Nu verwijzen we naar het resultaat van Voorbeeld 1, dat concludeert dat de coördinaten van een punt P ', symmetrisch met P en coördinaten (a, b), is (-a, -b). 

Maar in deze oefening heeft punt P coördinaten (x, y), dus zijn symmetrische p 'zal coördinaten x' = -x e y '= -y hebben. Dit vervangen in de symmetrische omtrekvergelijking is:

Kan u van dienst zijn: rhomboid: kenmerken, hoe u de perimeter en het gebied kunt verwijderen

(-X)² + (-En)² = R²

Die gelijkwaardig is aan: x²+ En² = R², Concluderend dat de centrale symmetrische van een cirkel ten opzichte van zijn centrum de omtrek zelf is.

- Oefening 2

Demonstreer op een geometrische manier dat centrale symmetrie de hoeken behoudt.

Oplossing

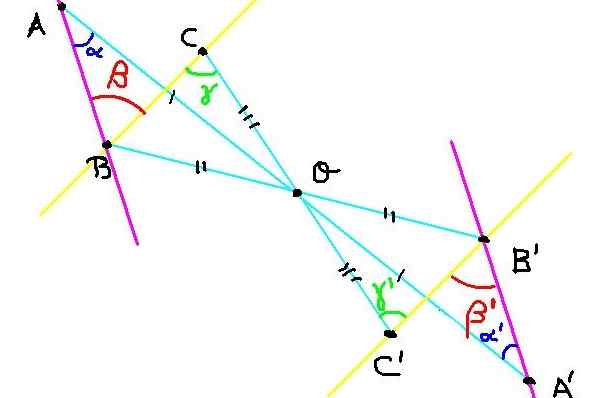Figuur 4. Constructie van symmetrische punten voor oefening 2. Bron: f. Zapata.

Er zijn drie punten A, B en C in het vliegtuig. Zijn symmetrische a ', b' en c 'zijn gebouwd met betrekking tot het midden van symmetrie of, zoals getoond in figuur 4. 

Nu moeten we aantonen dat de hoek ∡abc = β dezelfde maat heeft als de hoek ∡a'b'c '= β' '.

Omdat C en C 'symmetrisch zijn, dan OC = OC'. Evenzo ob = ob 'y oa = oa'. Aan de andere kant, de hoek ∡boc = ∡b'oc 'omdat hij tegen het hoekpunt is.

Dan zijn de Triangles Boc en B'oc 'congruent voor het hebben van een gelijke hoek tussen twee kanten gelijk.

Omdat BOC congruent is met B'oc 'dan de hoeken  γ En γ ' Ze zijn gelijk. Maar deze hoeken, naast het vervullen γ = γ ' Ze zijn intern alternatief tussen de lijnen van BC en B'c, wat impliceert dat de BC -lijn parallel is aan B'c '.

Evenzo is BAA congruent om dat te b'oa van wat wordt gevolgd α = α ' . Maar  α En α ' Het zijn interne alternatieve hoeken tussen de lijnen Ba en B'a ', waarvan wordt geconcludeerd dat de lijn BA parallel is aan b'a'.

Omdat de hoek ∡abc = β zijn parallelle zijden heeft met de hoek ∡a'b'c '= β' en ook beide acuut zijn, wordt geconcludeerd dat:

∡abc = ∡a'b'c '= β = β' '

Op deze manier aantonen dat centrale symmetrie de maat van hoeken behoudt.

Referenties

1. Baldor, J. NAAR. 1973.Flat and Space Geometry. Midden -Amerikaans cultureel. 
2. Wiskundige wetten en formules. Hoek meetsystemen. Opgehaald uit: ingemecanica.com.
3. Wentworth, G. Planeetgeometrie. Hersteld van: Gutenberg.borg.
4. Wikipedia. Centrale symmetrie. Hersteld van: is.Wikipedia.com
5. Wikipedia. Transportband. Hersteld van: is.Wikipedia.com
6. Zapata F. Interne en externe conjugaathoeken. Opgehaald uit: lifer.com