Null -hoek definitie en kenmerken, voorbeelden, oefeningen

Hij nulhoek Het is degene wiens maatregel 0 waard is, zowel in graden als in radianen of andere hoeken meetsysteem. Daarom mist het amplitude of opening, zoals die tussen twee parallelle lijnen.

Hoewel de definitie vrij eenvoudig klinkt, is de nulhoek erg nuttig in veel fysica- en engineeringapplicaties, evenals in navigatie en ontwerp.

Figuur 1. Tussen de snelheid en versnelling van de auto is er een nulhoek, daarom gaat de auto sneller en sneller. Bron: Wikimedia Commons.

Er zijn fysieke hoeveelheden die parallel moeten worden uitgelijnd om bepaalde effecten te bereiken: als een auto recht op een snelweg en tussen de snelheidsvector beweegt v en de vectorversnelling naar Er is 0º, de auto neemt toe.

In de volgende figuur verschijnen verschillende soorten hoek, waaronder de nulhoek rechts. Zoals te zien is, mist hoek 0 amplitude of opening.

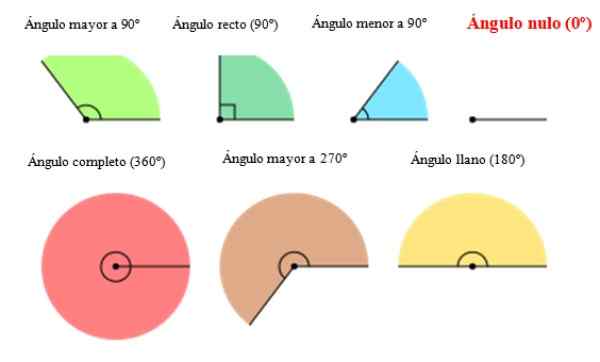Figuur 2. Soorten hoek, inclusief de nulhoek. Bron: Wikimedia Commons. Orias [cc by-sa (https: // creativeCommons.Org/licenties/by-sa/3.0)].[TOC]

Voorbeelden van nulhoeken

Het is bekend dat parallelle lijnen een hoek van een hoek vormen. Wanneer u een horizontale lijn hebt, is dit parallel aan de x -as van het Cartesiaanse coördinatensysteem, daarom is de neiging ervan met betrekking tot het 0. Met andere woorden, horizontale lijnen hebben een nulhelling.

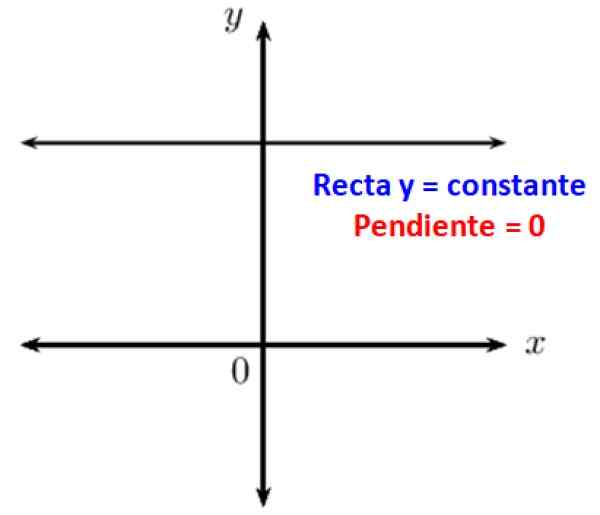figuur 3. Horizontale lijnen hebben een nul in behandeling. Bron: f. Zapata.

Ook de trigonometrische redenen van de nulhoek zijn 0, 1 of oneindig. Daarom is de nulhoek aanwezig in veel fysieke situaties waarbij operaties met vectoren betrokken zijn. Deze redenen zijn:

Kan u van dienst zijn: ordelijk paar

-Sen 0º = 0

-cos 0º = 1

-Tg 0º = 0

-Sec 0º = 1

-Schade 0º → ∞

-CTG 0º → ∞

En ze zullen nuttig zijn om enkele voorbeelden te analyseren van situaties waarin de aanwezigheid van de nulhoek een fundamentele rol speelt:

- Effecten van nulhoek op fysieke magnitudes

Som van vectoren

Wanneer twee vectoren parallel zijn, is de hoek tussen hen nietig, zoals te zien in figuur 4 van hierboven. In dit geval wordt de som van beide uitgevoerd door de ene na de andere te plaatsen en is de grootte van de vectorsom de som van de magnitudes van de addends (figuur 4b).

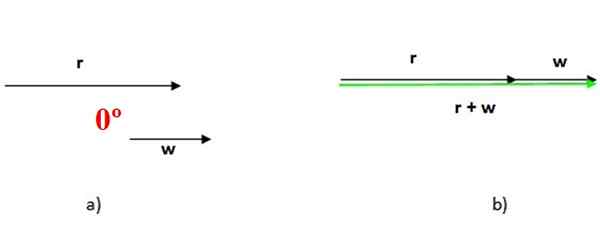Figuur 4. Som van parallelle vectoren, in dit geval is de hoek ertussen een nulhoek. Bron: f. Zapata.

Wanneer twee vectoren parallel zijn, is de hoek tussen hen nietig, zoals te zien in figuur 4 van hierboven. In dit geval wordt de som van beide uitgevoerd door de ene na de andere te plaatsen en is de grootte van de vectorsom de som van de magnitudes van de addends (figuur 4b)

Het koppel of koppel

Het koppel of koppel veroorzaakt de rotatie van een lichaam. Het hangt af van de grootte van de uitgeoefende kracht en hoe deze van toepassing is. Een zeer representatief voorbeeld is de Engelse sleutel van de figuur.

Om het beste omloopeffect te bereiken, is Force loodrecht op de belangrijkste handgreep van toepassing, hetzij omhoog of omlaag, maar rotatie wordt niet verwacht als de kracht parallel is aan de handgreep.

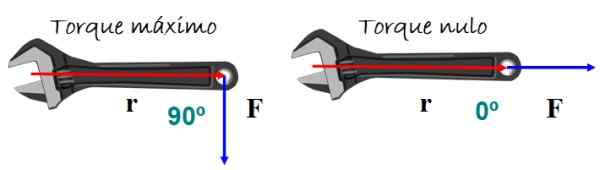Figuur 5. Wanneer de hoek tussen de positie en de sterkte -vectoren nietig is, vindt het koppel niet plaats en daarom is er geen draai -effect. Bron: f. Zapata.

Wiskundig het koppel τ Het wordt gedefinieerd als het vector of het kruisproduct tussen de vectoren R (Positievector) en F (Krachtvector) van figuur 5:

Kan u van dienst zijn: statistische takken

τ = r X F

De omvang van het koppel is:

τ = r f sen θ

Zijn θ de hoek tussen R En F. Wanneer sin θ = 0 is het koppel nietig, in dat geval θ = 0º (of ook 180º).

Elektrische veldstroom

De elektrische veldstroom is een scalaire grootte die afhangt van de intensiteit van het elektrische veld, evenals de oppervlakte -oriëntatie waardoor het kruist.

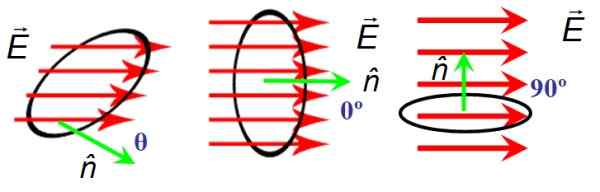
In figuur 6 is er een cirkelvormig oppervlak van gebied A waardoor de elektrische veldlijnen passeren EN. De oppervlakte -oriëntatie wordt gegeven door de normale vector N. Links het veld en de normale vector vormen een willekeurige willekeurige hoek θ, in het midden vormen ze een nulhoek en de rechter zijn loodrecht.

Wanneer EN En N Ze staan ​​loodrecht, de veldlijnen kruisen het oppervlak niet en daarom is de stroom nul, terwijl de hoek tussen EN En N Het is nietig, de lijnen kruisen het oppervlak volledig.

Door de elektrische veldstroom aan te duiden door de Griekse letter φ (leest "Fi"), de definitie ervan voor een uniform veld zoals in de figuur, blijft het als volgt:

Φ = EN•NNAAR

Het punt in het midden van beide vectoren geeft het punt- of scalaire product aan, dat afwisselend definieert:

Φ = EN•NA = eacosθ

Vetgedrukte en pijlen boven de letter zijn middelen om onderscheid te maken tussen een vector en de omvang ervan, die wordt aangegeven met normale letters. Sinds cos 0 = 1 is de stroom maximaal wanneer EN En N Ze zijn parallel.

Figuur 6. De elektrische veldstroom hangt af van de oriëntatie tussen het oppervlak en het elektrische veld. Bron: f. Zapata.

Opdrachten

- Oefening 1

Twee krachten P En Q Ze werken tegelijkertijd op een tijdige object X, beide krachten vormen aanvankelijk een hoek θ tussen hen. Wat gebeurt er met de grootte van de resulterende kracht wanneer θ afneemt totdat deze is geannuleerd?

Kan u van dienst zijn: evaluatie van functies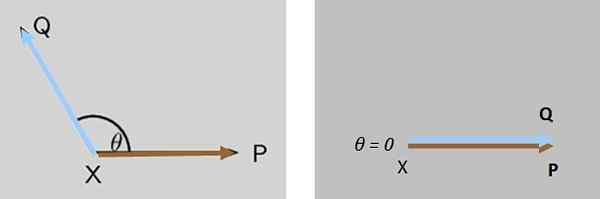 Figuur 7. De hoek tussen twee krachten die op een lichaam werken, neemt af totdat de grootte van de resulterende kracht zijn maximale waarde verwerft, wordt in dit geval geannuleerd. Bron: f. Zapata.

Oplossing

De omvang van de resulterende kracht Q + P Het neemt geleidelijk toe tot het maximaal is wanneer Q En P Ze zijn totaal parallel (figuur 7 recht).

- Oefening 2

Geef aan of de nulhoek een oplossing is van de volgende trigonometrische vergelijking:

cos 2x = 1 + 4se x

Oplossing

Een trigonometrische vergelijking is er een waarin het onbekende deel uitmaakt van het argument van een trigonometrische reden. Om de voorgestelde vergelijking op te lossen, is het handig om gebruik te maken van de formule voor de cosinus met dubbele hoek:

cos 2x = cos² X - Sen² X

Omdat op deze manier het argument aan de linkerkant wordt X in plaats van 2x. Dus:

zomaar² X - Sen² x = 1 + 4Sen x

Aan de andere kant cos² X + sen² x = 1, dus:

zomaar² X - Sen² X = COS² X + sen² X + 4Sen x

De term cos² X is geannuleerd en blijft:

- Sen² X = Sen² X + 4Sen X → - 2Sen² X - 4Senx = 0 → 2Sen² X + 4Senx = 0

Nu wordt de volgende variabele verandering aangebracht: senx = u en de vergelijking wordt omgezet in:

2U² + 4U = 0

2U (u+4) = 0

Wiens oplossingen zijn: u = 0 en u = -4. Retourneren van de verandering zouden we twee mogelijkheden hebben: sin x = 0 en senx = -4. Deze laatste oplossing is niet levensvatbaar, omdat de borst van een hoek tussen -1 en 1 ligt, dus we blijven achter met het eerste alternatief:

sin x = 0

Daarom is x = 0º een oplossing, maar dient ook elke hoek waarvan de sinus 0 is, die ook 180º (π radianen), 360º (2 π radialen) kan zijn en ook de respectieve negatieven.

De meest algemene oplossing van de trigonometrische vergelijking is: x = kπ waarbij k = 0, ± 1, ± 2, ± 3, .. . k Een geheel getal nummer.

Referenties

1. Baldor, een. 2004. Flat and Space Geometrie met trigonometrie. Culturele publicaties s.NAAR. van C.V. Mexico.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 3. Deeltjessystemen. Uitgegeven door Douglas Figueroa (USB).
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 5. Elektrische interactie. Uitgegeven door Douglas Figueroa (USB).
4. Onlinemathlearning. Soorten hoeken. Opgehaald uit: OnlinemathLearning.com.
5. Zill, D. 2012. Algebra, trigonometrie en analytische geometrie. McGraw Hill Inter -American.