Relatieve beweging in een dimensie, in twee dimensies, oefeningen

Hij relatieve beweging van een deeltje of een object is degene waargenomen met betrekking tot een bepaald referentiepunt dat de waarnemer heeft gekozen, die kan worden gefixeerd of verplaatst. Snelheid verwijst altijd naar een coördinatensysteem dat wordt gebruikt om het te beschrijven.

Bijvoorbeeld, de co -pilot van een bewegende auto en die comfortabel in zijn stoel reist, is in rust ten opzichte van de bestuurder, maar hij is niet voor een waarnemer die op het trottoir staat dat de auto ziet passeren.

Figuur 1. Vliegtuigen behouden een bepaalde relatieve snelheid tussen hen bij het oefenen van acrobatiek. Bron: Pixabay.

Dan is de beweging altijd relatief, maar het gebeurt dat het coördinaat- of referentiesysteem meestal wordt gekozen, met zijn oorsprong in de aarde of de grond, een plaats die als stationair wordt beschouwd. Op deze manier richt de bezorgdheid zich op het beschrijven van de beweging van het onderzochte object.

Is het mogelijk om de snelheid van de slaapco -driver te beschrijven ten opzichte van een passagier die in een andere auto reist? Het antwoord is ja. Er is de vrijheid om de waarde van (x te kiezen_of, En_of, Z_of): De oorsprong van het referentiesysteem. De selectie is willekeurig en hangt af van de voorkeur van de waarnemer, evenals het gemak dat u voor de oplossing van het probleem biedt.

[TOC]

Relatieve beweging in een dimensie

Wanneer de beweging langs een rechte lijn gaat, hebben mobiele telefoons snelheden in dezelfde richting of in de tegenovergestelde richting, beide gezien door een waarnemer die op het land staat (t). Verlaat de waarnemer met betrekking tot mobiele telefoons? Ja, met dezelfde snelheid die ze dragen, maar in de tegenovergestelde richting.

Hoe gaat een mobiele beweging ten opzichte van de ander? Om erachter te komen dat de snelheden worden toegevoegd vector.

Het kan je van dienst zijn: Pluto (Dwarf Planet)

-Opgelost voorbeeld 1

In verwijzing naar de getoonde figuur, geef de relatieve snelheid van de auto 1 aan met betrekking tot de auto 2 in elke situatie.

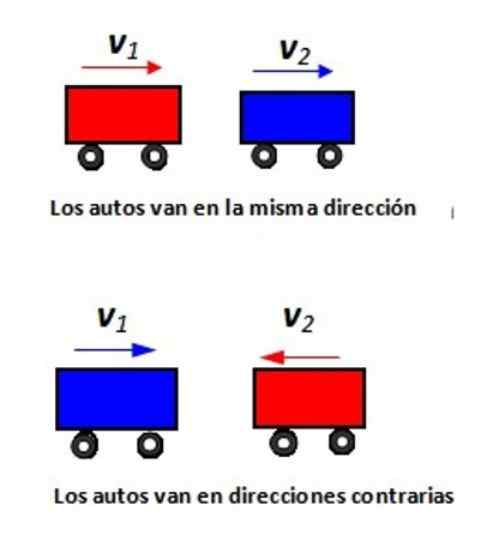Figuur 2. Twee auto's gaan op een rechtlijnige weg: a) in dezelfde richting en b) in tegengestelde richtingen.

Oplossing

We zullen een positief teken toewijzen aan de snelheden rechts en een negatief teken aan de linkerkant. Als een mobiel naar rechts gaat met 80 km/u, ziet een passagier in deze mobiel de waarnemer op de grond naar - 80 km/u.

Stel dat alles gebeurt langs de X -as. In de volgende figuur beweegt de rode auto op +100 km/u (gezien vanaf t) en bereidt zich voor op de blauwe auto die reist op +80 km/u (ook gezien vanaf t). Met welke snelheid zie je een passagier de rode auto in de blauwe auto naderen?

De labels zijn: v _1/2 Auto 1 snelheid ten opzichte van 2, v_1/t Autosnelheid met betrekking tot T, v_T/2 Tafelsnelheid ten opzichte van 2. Vectoriaal toevoegen:

v_1/2 = v_1/t + v_T/2 = (+100 km/u - 80 km/u) X= 20 km/h X

We kunnen het zonder de vectornotatie. Let op de subscripts: beide aan de rechterkant vermenigvuldigen moet die links verkrijgen.

En wanneer ze zich in de tegenovergestelde richting bevinden? Nu v_1/t = + 80 km/u en v_2/t = -100 km/u, daarom V_T/2 = + 100 km/h. De passagier van de Auto Blue zal de rode auto zien naderen:

v_{1/2 =} v_1/t + v_T/2 = +80 km/h +100 km/h = 180 km/h

Relatieve beweging in twee en drie dimensies

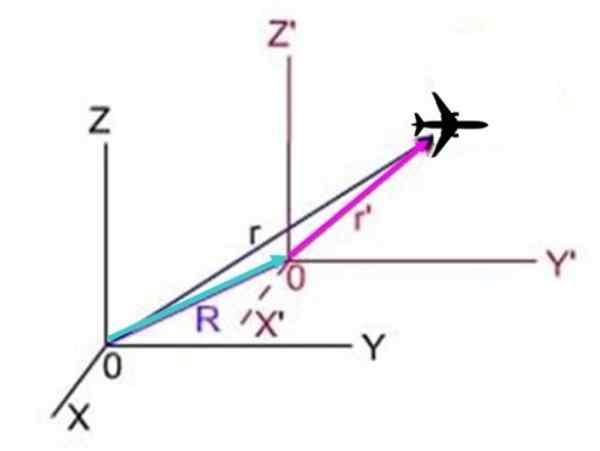
In het volgende schema, R Het is de positie van het vlak gezien vanuit het systeem X en Z, R'Het is de positie van het systeem X en Z ' En R Het is de positie van het systeem met een premie ten opzichte van het systeem zonder premium. De drie vectoren vormen een driehoek waarin R + R'= R, daarom R'= r - r.

figuur 3.- Het vlak beweegt met betrekking tot twee coördinatensystemen, op zijn beurt beweegt een van de systemen ten opzichte van de andere.

Omdat de afgeleide ten opzichte van de tijd van de positie precies de snelheid is, resultaten:

Kan u van dienst zijn: parabolisch schot: kenmerken, formules en vergelijkingen, voorbeelden

v'= v - of

In deze vergelijking v'Het is de snelheid van het vlak ten opzichte van het systeem X en Z ', v is de snelheid ten opzichte van het systeem X en Z En of Het is de constante snelheid van het prime -systeem ten opzichte van het systeem zonder premies.

-Oefening opgelost 2 

Een vliegtuig bevindt zich in de noordelijke richting met een snelheid ten opzichte van de lucht van 240 km/u. Plots begint het wind van west naar oost te blazen met een snelheid van 120 km/ volgens de aarde.

Vind: a) de snelheid van het vlak ten opzichte van de aarde, b) de afwijking door de piloot c) de correctie die de piloot moet maken om rechtstreeks naar het noorden te kunnen wijzen en de nieuwe snelheid ten opzichte van land, eens De correctie is aangebracht.

Oplossing

a) De volgende elementen worden gedaan: vlak (a), aarde (t) en wind (v).

In het coördinatensysteem waarin het noorden de + en en de west-oostelijke richting is, zijn er + x, zijn er de gegeven snelheden en hun respectieve label (subscripts):

v _Av = 240 km/h (+En); v _V/t = 120 km/h (+X); v _Bij = ?

De adequate vector som is:

v _Bij = v _Av + v _V/t = 240 km/h (+En) + 120 km/u (+X))

De omvang van deze vector is: v _Bij = (240 ²+ 120²))^1/2 km/h = 268.3 km/h

b) θ = arctg (v _Av / V _V/t) = arctg (240 /120) = 63.4e ten noorden van het oosten of 26.6e noordoosten.

c) Om met deze wind naar het noorden te blijven, moet u de boog van het vliegtuig naar het noordwesten richten, zodat de wind hem rechtstreeks naar het noorden duwt. In dit geval zal de snelheid van het vlak dat vanuit de grond wordt gezien in de +zijn en, hoewel de snelheid van het vlak ten opzichte van de wind noordwest zal zijn (het is niet noodzakelijk 26.6e).

Kan u van dienst zijn: Bernoulli Stelling

Door Pythagoras Stelling:

v _Bij = (240 ²- 120²))^1/2 km/h = 207.8 km/h

α = arctg (v _V/t / V _Bij ) = arctg (120/207.8) = 30e noordwest

-Oefening opgelost 3

Een persoon heeft 2 minuten nodig om door een immobiele mechanische trap te lopen. Als de trap werkt, duurt de persoon 1 minuut om nog steeds te gaan. Hoe lang duurt de persoon wandelen en met de trap loopt?

Oplossing

Er zijn drie elementen om te overwegen: de persoon (p), de trap (e) en de grond (s), waarvan de relatieve snelheden zijn:

v_P/e : snelheid van de persoon met betrekking tot de ladder; v_IS: snelheid van de trap ten opzichte van de grond; v_P/s: De snelheid van de persoon ten opzichte van de grond.

Zoals van de grond wordt gezien door een vaste waarnemer, heeft de persoon die de trap (e) verlaagt een snelheid V _P/s gegeven door:

v _P/s = v_P/e + v_IS

De positieve zin is de trap af. Zijn T  de tijd die nodig is om te gaan lopen en L afstand. De omvang van de persoon v _P/s is:

v_P/s = L / t

T₁ Het is de tijd die nodig is om met de gestopt ladder naar beneden te gaan: V _P/e = L / t₁

En t₂ Degene die je nog steeds in beweging op de trap haalt: V _IS = L / t₂

Het combineren van uitdrukkingen:

L / t = l / t₁ + L / t₂

Numerieke waarden vervangen en opruimen T:

1 / t = 1 / t₁ + 1 / t₂ = 1/2 + 1/1 = 1.5

Dan t = 1/1.5 minuten = 40 seconden.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill. 84-88.
2. Figueroa, D. Fysieke serie voor wetenschap en engineering. Deel 3. Editie. Kinematica. 199-232.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6^e. ED. Prentice Hall. 62-64.
4. Relatieve beweging. Hersteld van: cursussen.Lumenarning.com
5. Wilson, J. 2011. Natuurkunde 10. Pearson Education. 166-168.