Rechtlijnige bewegingskenmerken, typen en voorbeelden

Hij rectilineale beweging Het is er een waarin de mobiel langs een rechte lijn beweegt en daarom in een dimensie passeert, daarom ook de naam van Unidimensionale beweging. Deze rechte lijn is de traject of pad gevolgd door het object dat beweegt. De auto's die langs de laan van figuur 1 reizen, volgen dit soort beweging.

Dit is het eenvoudigste bewegingsmodel dat kan worden voorgesteld. De dagelijkse bewegingen van mensen, dieren en dingen combineren vaak transfers in een rechte lijn met bewegingen langs bochten, maar sommigen observeren vaak sommige die uitsluitend rechte richtlijnen zijn.

Figuur 1. Auto's bewegen langs een rechtlijnige weg. Bron: Pixabay.

Hier zijn enkele goede voorbeelden:

- Wanneer u loopt langs een rechtlijnige baan van 200 -meter.

- Auto rijden op een rechte weg.

- Een object vrijelijk van een bepaalde hoogte laten vallen.

- Wanneer een bal verticaal wordt gegooid.

https: // giphy.com/gifs/j5XX3BYNAQV06WTOXQ

Nu wordt het doel van het beschrijven van een beweging bereikt door kenmerken op te geven zoals:

- Positie

- Verplaatsing

- Snelheid

- Versnelling

- Tijd.

Om een ​​waarnemer de beweging van een object te detecteren, is het noodzakelijk om een ​​referentiepunt (oorsprong O) te hebben en een specifiek adres te hebben ingesteld om te bewegen, wat de as kan zijn X, de as En of een ander.

Wat betreft het object dat beweegt, dit kan talloze manieren hebben. Er zijn in dit opzicht geen beperkingen, maar in alles wat volgt zal worden aangenomen dat de mobiel een deeltje is; een object dat zo klein is dat de afmetingen niet relevant zijn.

Het is bekend dat dit niet het geval is voor macroscopische objecten; Het is echter een model met goede resultaten in de beschrijving van de globale beweging van een object. Op deze manier kan een deeltje een auto, een planeet, een persoon of een ander object zijn dat beweegt.

We zullen beginnen met onze studie van rechtlijnige kinematica met een algemene benadering van de beweging en dan zullen bepaalde gevallen worden bestudeerd als al benoemd.

[TOC]

Algemene kenmerken van de rechtlijnige beweging

De volgende beschrijving is algemeen en van toepassing op elk type van één dimensionale beweging. Het eerste is om een ​​referentiesysteem te kiezen. De lijn waarlangs de beweging plaatsvindt zal de as zijn X. De parameters van de beweging:

Positie

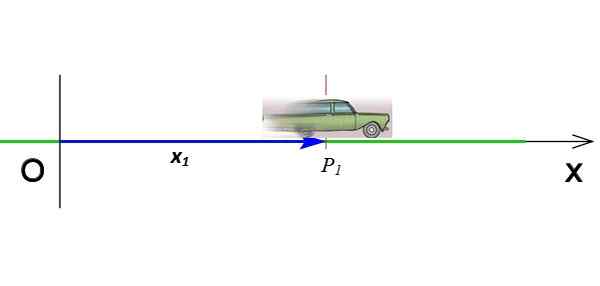Figuur 2. Positie van een mobiel die op de X -as beweegt. Bron: Wikimedia Commons (aangepast door F. Zapata).

Het is de vector die gaat van de oorsprong tot het punt waarop het object in een oogwenk wordt gegeven. In figuur 2, de vector X₁ Geeft de positie van de mobiel aan wanneer deze in de coördinaat staat P₁ en na verloop van tijd T₁. De positie vector -eenheden in het internationale systeem zijn meter.

Verplaatsing

Verplaatsing is de vector die de positiewijziging aangeeft. In figuur 3 is de auto van de positie gegaan P₁ naar de positie P₂, Daarom is de verplaatsing de verplaatsing δX = X₂ - X₁. Verplaatsing is de aftrekking van twee vectoren, het wordt gesymboliseerd met de Griekse letter δ ("delta") en is op zijn beurt een vector. Zijn eenheden in het internationale systeem zijn meter.

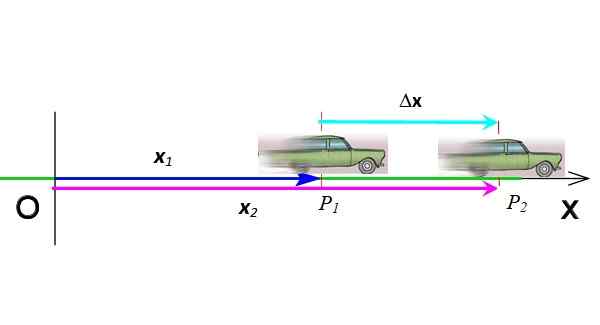figuur 3. Vectorverplaatsing. Bron: voorbereid door F. Zapata.

Vectoren worden aangeduid met vetgedrukt in gedrukte tekst. Maar als je op dezelfde dimensie bent, kun je indien gewenst doen zonder de vectornotatie.

Kan u van dienst zijn: takken van klassieke en moderne fysica

Afgelegde afstand

Afstand D Toured door het bewegende object is de absolute waarde van de verplaatsingsvector:

D = ΙXΙ = δX

Omdat het een absolute waarde is, is de afgelegde afstand altijd groter dan of gelijk aan 0 en zijn eenheden hetzelfde als die van positie en verplaatsing. Absolute waarde Notatie kan worden gedaan met modulebars of eenvoudigweg de gewaagde letter in gedrukte tekst verwijderen.

Gemiddelde snelheid

Hoe snel verandert de positie? Er zijn langzame en snelle mobiele telefoons. De sleutel is altijd de snelheid geweest. Om deze factor te analyseren, wordt de positie geanalyseerd X Functie van de tijd T.

De gemiddelde snelheid v_M (Zie figuur 4) Het is de helling van de drooglijn (fuchsia) naar de curve X Vs T en biedt wereldwijde informatie over mobiele verplaatsing in het overwogen tijdsinterval.

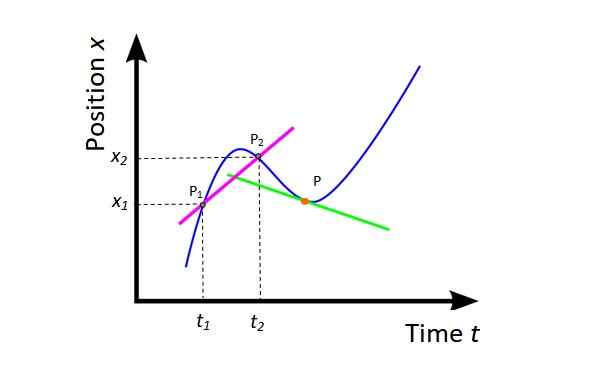Figuur 4. Gemiddelde snelheid en onmiddellijke snelheid. Bron: Wikimedia Commons, aangepast door F. Zapata.

v_M = (X₂ - X₁) / (T₂ -T₁) = ΔX / ΔT

De gemiddelde snelheid is een vector waarvan eenheden in het internationale systeem zijn meters /tweede ((Mevr)).

Onmiddellijke snelheid

De gemiddelde snelheid wordt berekend door een meetbaar tijdsinterval te nemen, maar informeert niet over wat er binnen het genoemde interval gebeurt. Om de snelheid op elk moment te weten, moet je het tijdsinterval erg klein maken, wiskundig is het gelijk aan doen:

Δt → 0

De vergelijking wordt eerder gegeven voor gemiddelde snelheid. Op deze manier wordt de onmiddellijke snelheid of gewoon snelheid verkregen:

Geometrisch is de afgeleide van de positie ten opzichte van de tijd de helling van de lijn die naar de curve raakt X Vs T op een bepaald punt. In figuur 4 is het punt oranje en de raaklijn is groen. De momentane snelheid op dit punt is de helling van die lijn.

Snelheid

Snelheid wordt gedefinieerd als de absolute waarde- of snelheidsmodule en is altijd positief (signalering, wegen en snelwegen zijn altijd positief, nooit negatief). De termen "snelheid" en "snelheid" kunnen dagelijks worden gebruikt, maar in de natuurkunde is het onderscheid tussen vector en klimmen noodzakelijk.

v = ΙvΙ = v

Gemiddelde versnelling en onmiddellijke versnelling

De snelheid kan veranderen in de loop van de beweging en de realiteit is dat deze naar verwachting dit zal doen. Er is een omvang die deze verandering kwantificeert: versnelling. Als we opmerken dat snelheid de positiewijziging is ten opzichte van de tijd, is versnelling de verandering van snelheid ten opzichte van de tijd.

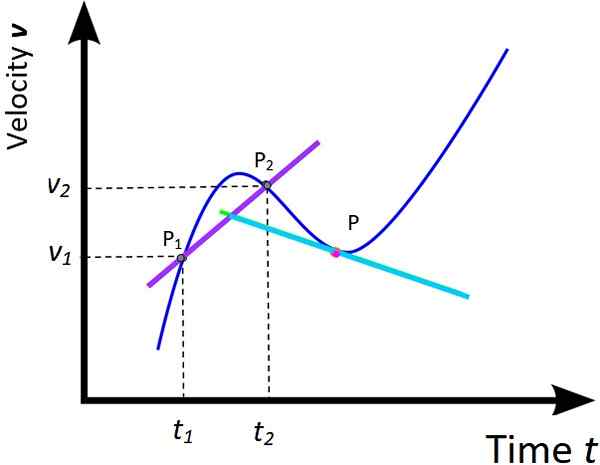Figuur 5. Gemiddelde versnelling en onmiddellijke versnelling. Bron: Wikimedia Commons, aangepast door F. Zapata.

De behandeling gegeven aan de grafiek van X Vs T Van de twee vorige secties kunnen worden uitgebreid tot de overeenkomstige grafiek van v Vs T. Bijgevolg worden een gemiddelde versnelling en onmiddellijke versnelling gedefinieerd als:

naar_M = (v₂ - v₁) / (T₂ -T₁) = Δv / ΔT  (In afwachting van de verblijf)

Versnelling en vertraging

In de ene -dimensionale beweging hebben vectoren per conventie positieve of negatieve tekenen terwijl ze op de een of andere manier gaan. Wanneer de versnelling dezelfde betekenis heeft als de snelheid, verhoogt deze de grootte, maar wanneer het de tegenovergestelde zin heeft en de snelheid zijn magnitude vermindert. Er wordt dan gezegd dat de beweging is vertraagd.

Kan u van dienst zijn: Leyden Bottle: onderdelen, werking, experimenten

Jongens

De classificatie van rectilinese bewegingen wordt meestal gedaan op basis van:

- Of de versnelling al dan niet constant is.

- De beweging gaat langs een horizontale of verticale lijn.

Beweging met constante versnelling

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

Wanneer de versnelling constant is, is de gemiddelde versnelling naar_M Het is gelijk aan onmiddellijke versnelling naar En er zijn twee opties:

- Dat de versnelling 0 waard is, in welk geval de snelheid constant is en een uniforme rechtlijnige beweging of MRU heeft.

- Constante versnelling verschilt van 0, waarbij snelheid in de loop van de tijd lineair groeit of afneemt (de rechtlijnige beweging uniform gevarieerd of MRUV):

Waar v_F  En T_F Ze zijn respectievelijk de laatste snelheid en tijd, en v_of En T_of Ze zijn initiële snelheid en tijd. Ja T_of = 0, Bij het wissen van de uiteindelijke snelheid heb je de vergelijking al bekend voor de laatste snelheid:

v_F = V_of + BIJ

Voor deze beweging zijn de volgende vergelijkingen ook geldig:

- Positie afhankelijk van de tijd: x = x_of + v_{of .}t +½ bij²

- Snelheid afhankelijk van de positie: v_F² = V_of² + 2e.ΔX  (Met δx = x - x_of))

Horizontale bewegingen en verticale bewegingen

De horizontale bewegingen zijn die die langs de horizontale as of x -as passeren, terwijl de verticale mensen het langs de as en as doen. Verticale bewegingen onder de werking van de zwaartekracht zijn de meest voorkomende en interessante.

In de vorige vergelijkingen wordt het genomen A = G = 9.8 m/s² verticaal gericht, richting die bijna altijd is gekozen met een negatief teken.

Op deze manier, v_F = V_of + BIJ Het transformeert in v_F = V_of - GT En als de initiële snelheid 0 is omdat het object vrij is gevallen, is het verder vereenvoudigd v_F = - GT. Zolang er geen rekening wordt gehouden met luchtweerstand, natuurlijk.

Opgeloste voorbeelden

voorbeeld 1

Op punt wordt een klein pakket vrijgegeven zodat het langs de transporter beweegt met schuifwielen ABCD weergegeven in de figuur. Terwijl het afdalen door de hellende secties AB en CD, draagt ​​het pakket een versnelling van 4,8 m/s², Terwijl in het horizontale gedeelte BC een constante snelheid handhaaft.

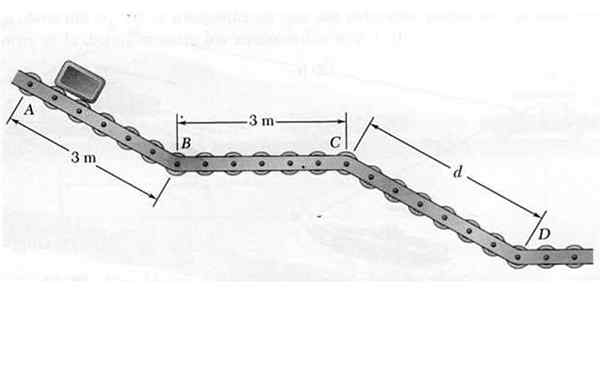Figuur 6. Het pakket dat op het schuifpad van het opgeloste voorbeeld beweegt 1. Bron: zelf gemaakt.

Wetende dat de snelheid waarmee het pakket bij D bereikt 7,2 m/s is, bepaalt u:

a) de afstand tussen C en D.

b) de tijd die het pakket nodig heeft om het einde te bereiken.

Oplossing

De beweging van het pakket wordt uitgevoerd in de drie getoonde rechtlijnige secties en om de gevraagde te berekenen, is de snelheid vereist op punten B, C en D. Laten we elke sectie afzonderlijk analyseren:

Sectie AB

Omdat de tijd niet beschikbaar is in dit gedeelte, zal deze worden gebruikt v_F² = V_of² + 2e.ΔX  Met Vo = 0:

v_F² = 2a.Δx → v_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/S² → v_F  = 5.37 m/s = V_B

De tijd die het pakket nodig heeft om de sectie AB te reizen is:

T_Aab = (v_F - v_of) /A = 5.37 m/s/4,8 m/s² = 1.19 s

Sectie BC

De snelheid in sectie BC is daarom constant v_B = V_C = 5.37 m/s. De tijd die het pakket nodig heeft om dit gedeelte te reizen is:

Kan u van dienst zijn: Lichtbreking: elementen, wetten en experiment

T_BC = Afstand _BC  / V_B = 3 m/ 5.37 m/s = 0.56 s

CD -sectie

De eerste snelheid van deze sectie is v_C = 5.37 m/s, De laatste snelheid is v_D = 7,2 m/s, via v_D²  = V_C² + 2. naar. D De waarde van D:

D = ((v_D²  - v_C²)/2.A = ((7.2²  - 5.37²)/2 X 4.8 m = 2.4 m

Tijd wordt berekend als:

T_{CD =} (v_D  - v_C)/A = ((7.2- 5.37)/ 4.8 s = 0.38 s.

De antwoorden op de gestelde vragen zijn:

a) d = 2.4 m

b) Reistijd is T_Aab + T_BC + T_CD = 1.19 S +0.56 S +0.38 s = 2.13 s.

Voorbeeld 2

Een persoon is onder een horizontale poort die aanvankelijk open is en 12 m hoog is. De persoon lanceert verticaal een object naar de poort met een snelheid van 15 m/s.

Het is bekend dat de poort 1,5 seconden sluit nadat de persoon het object heeft gelanceerd vanaf een hoogte van 2 meter. Luchtweerstand zal niet in aanmerking worden genomen. Beantwoord de volgende vragen, rechtvaardigen:

a) slaagt u erin het object door de poort te geven voordat het sluit?

b) Zal het object ooit tegen de gesloten poort botsen? Indien bevestigend, wanneer gebeurt het??

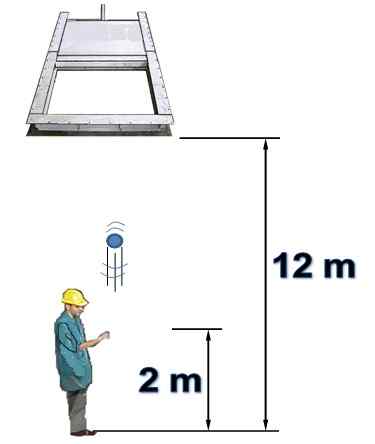Figuur 7. Een object wordt verticaal gestart (opgelost voorbeeld 2). Bron: zelf gemaakt.

Antwoord op)

Er zijn 10 meter tussen de beginpositie van de bal en de poort. Het is een verticale lancering, waarin dit adres als positief wordt beschouwd.

U kunt de snelheid ontdekken die het draagt ​​wanneer u op dit punt aankomt, met dit resultaat de tijd die nodig is om het te doen en te vergelijken met de sluitingstijd van de poort, die 1 is.5 seconden:

v_F ²= V_of ²- 2.G. Δen → v_F = (15² - 2 X 9.8 X10)^1/2 M = 5.39 m/s

T = (v_F - v_of) /g = (5.39 - 15) / (-9.8) S = 0.98 s

Omdat deze keer minder is dan 1.5 seconden, dan wordt geconcludeerd dat het object minstens eenmaal door de poort kan gaan.

Antwoord b)

We weten al dat het object het beheert. De snelheid, wanneer deze op de hoogte van de poort bereikt, heeft dezelfde grootte als wanneer deze omhoog gaat, maar in de tegenovergestelde richting. Werk daarom met -5.39 m/s en de tijd die nodig is om deze situatie te bereiken is:

T = (v_F - v_of) /G = (-5.39 - 15) / (-9.8) S = 2.08 s

Omdat de poort alleen open blijft voor 1.5 s, het is duidelijk dat het geen tijd heeft om te passeren voordat het sluit, omdat het het gesloten vindt. Het antwoord is: het object als het na 2 met de gesloten poort botst.08 seconden nadat het is vrijgelaten, wanneer het in afdaling komt.

Referenties

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).69-116.
2. Giancoli, D. Natuurkunde. (2006). Principes met toepassingen. 6^e Editie. Prentice Hall. 22-25.
3. Kirkpatrick, l. 2007. Natuurkunde: een blik op de wereld. 6^ta Afgekort editie. Cengage leren. 23 - 27.
4. Resnick, r. (1999). Fysiek. Deel 1. Derde editie in het Spaans. Mexico. Continental Editorial Company s.NAAR. van C.V. 21-22.
5. Rex, a. (2011). Fundamentals of Physics. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14^e. ED. Deel 1. 50 - 53.
7. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7^ma. Editie. Mexico. Cengage Learning Editors. 23-25.
8. Serway, r., Vulle, c. (2011). Fundamentals of Physics. 9^NA ED. Cengage leren. 43 - 55.
9. Wilson, J. (2011). Natuurkunde 10. Pearson Education. 133 - 149.