Pendulaire beweging

Wat is pendulaire beweging?

Hij Pendulaire beweging Het is een slingerende beweging gemaakt door een min of meer zwaar object, een slinger genoemd, opgehangen door een licht touw of staaf, gefixeerd aan het andere uiteinde.

De slinger wordt een initiële impuls verleend en mag op deze manier oscilleren, op deze manier beschrijft het object retourbogen. Dit is het principe van de werking van slingerhorloges, schommels, schommelstoelen en Metronomen van slinger, gebruikt om de tijden in muziek te markeren.

Pendulum oscillerend, waaruit snelheid en versnelling toont (Wikipedia.org)

Er wordt gezegd dat in 1581 Galileo Galilei de zwaai van een lamp in de kathedraal van Pisa heeft waargenomen, waarmee hij opmerkte dat, hoewel de amplitude van de kandelaars -oscillatie afnam vanwege wrijving met de lucht, niet de duur van de duur van de duur van de duur van de duur van de cyclus.

Dit trok de aandacht van Galileo, die besloot door te gaan met de studie en vastbesloten dat de slingerperiode niet afhankelijk is van het deeg, maar van de vierkantswortel van de lengte van het touw, zoals later zal worden gezien.

Kenmerken van de pendelende beweging

Een slinger is heel gemakkelijk te bouwen, omdat het voldoende is met een loodrecht op een katoenen draad en vasthoudt aan de andere kant met je vingers of door het te binden aan een ondersteuning als een nagel.

Na de kleine initiële impuls is het gewicht verantwoordelijk voor het oscilleren van de slinger, hoewel de wrijving de amplitude van de beweging afneemt, totdat deze eindelijk ophoudt.

Het belangrijkste kenmerk van de Pendular Movement is om repetitief te zijn, omdat het een beweging van Sway is. Nu, om uw studie te vergemakkelijken, is het handig om enkele vereenvoudigingen te maken om zich te concentreren op een eenvoudiger model, de genaamd de eenvoudige slinger.

De eenvoudige slinger

Het kind in de schommel kan worden gemodelleerd als een eenvoudige slinger

Het is een ideaal systeem dat bestaat uit een loodrecht, beschouwd als een punctuele massa M, onderworpen aan een licht en niet -uitgewend touw van lengte L. De kenmerken van dit systeem zijn:

• Een repetitieve en periodieke beweging hebben, bestaande uit heen en weer gaan van een boog van straalomtrek gelijk aan l.
• Houdt geen rekening met wrijving.
• De amplitude van de beweging is klein (< 5º).
• De periode is onafhankelijk van de massa M, En het hangt uitsluitend af van lengte L van de slinger.

Kan u van dienst zijn: resulterende vector: berekening, voorbeelden, oefeningen

Formules en vergelijkingen

Het volgende is een eenvoudig slinger diagram, waarop twee krachten handelen: het gewicht P van grootte Mg, die verticaal naar beneden is gericht en de spanning T Aan het touw. Ze worden niet beschouwd als wrijving.

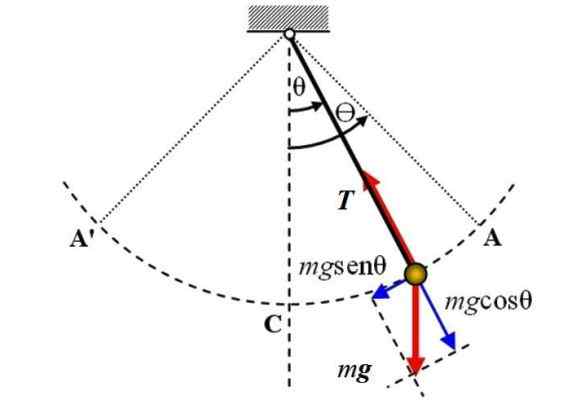Gratis lichaamsdiagram van de eenvoudige slinger. Bron: Wikimedia Commons.

De referentieas is de verticale as en valt samen met de positie θ = 0, van daaruit wordt de hoekverplaatsing θ gemeten, hetzij in de ene of de andere richting. Het teken + kan aan de rechterkant in de figuur worden toegewezen.

Om de slingerbeweging te bestuderen, wordt een coördinatensysteem gekozen met de oorsprong in de slinger zelf. Dit systeem heeft een tangentiële coördinaat naar de A'ca -omtrekboog beschreven door de slinger, evenals een radiale coördinaat, gericht op het midden van het traject.

Op het moment dat in de figuur wordt getoond, beweegt de slinger naar rechts, maar de tangentiële component van de zwaartekracht, F genoemd_T, is verantwoordelijk voor het teruggeven. Het wordt gewaarschuwd voor de figuur dat deze component een gevoel heeft in strijd met de beweging.

Wat betreft de spanning op het touw, deze is in balans met de component van het gewicht Mgcosθ.

De netto kracht is dan degene die F wordt genoemd_T En door de tweede wet van Newton is het gelijk aan het product Mass × versnelling, En dit is op zijn beurt de tweede afgeleid van lineaire verplaatsing S, Wat wordt de boog afgelegd door de slinger. Dus:

Hoekverplaatsing 

De vergelijking moet worden uitgedrukt in termen van een enkele variabele, die onthouden dat hoekverplaatsing θ en de bewaarde boog gerelateerd zijn door vergelijking:

Het kan u van dienst zijn: tweede wet van thermodynamica: formules, vergelijkingen, voorbeelden

S = L.θ

De massa wordt aan beide zijden geannuleerd en als de amplitude klein is, is de hoek θ ook, op een manier, de volgende aanpak geldig:

sin θ ≈ θ

Hiermee wordt de volgende differentiaalvergelijking voor variabele θ (t) verkregen:

Deze vergelijking is zeer eenvoudig op te lossen, omdat de oplossing een functie is waarvan de tweede afgeleide de functie zelf is. Er zijn drie alternatieven: een cosinus, één borst of een exponentiële. De cosinusfunctie wordt gekozen voor hoekverplaatsing θ (t), omdat het een goed bekende en gemakkelijk te hanteren functie is.

De lezer kan twee keer controleren, dat de volgende functie voldoet aan de differentiaalvergelijking:

θ (t) = θ_M cos (ωt + φ)

Waar θ_M Het is maximale hoek dat de slinger beweegt ten opzichte van verticale en hoekfrequentie ω is:

De constante φ wordt toegevoegd om algemeenheid aan de oplossing te geven en past in overeenstemming met de beginvoorwaarden.

Periodevergelijking

De T -periode van de beweging is de tijd die nodig is om een ​​cyclus uit te voeren en wordt gedefinieerd als:

Ω vervangen:

Zoals eerder vastgesteld, hangt de periode niet af van de massa van de slinger, maar alleen van de lengte.

Voorbeelden van pendelende beweging

Hartslagmaat

Galileo had het optreden van het meten van de hartslag van mensen, waarbij de lengte van de slinger werd aangepast tot de periode met de pulsaties van het hart van een persoon samenvalt.

De slingerklok

Dit is ongetwijfeld een van de meest bekende voorbeelden van de pendulaire beweging. De productie van pendelhorloges heeft zowel wetenschap als kunst. De Nederlandse fysicus Christian Huygens (1629-1695) ontwikkelde de eerste pendelwacht in 1656, gebaseerd op de studie die jaren geleden werd gemaakt door Galileo.

Kan u van dienst zijn: golvende optica

Foucault's slinger

Foucault -slinger. Bron: Wikimedia Commons.

Het is een enigszins andere slinger dan hierboven beschreven, omdat het in staat is om in elk verticaal vlak te draaien. Het is gemaakt door de Franse natuurkundige Léon Foucault (1819-1868) en wordt gebruikt om de rotatie van de aarde te visualiseren.

Oefening opgelost

Een eenvoudige slinger passeert elke 0.5 s voor de evenwichtspositie. Wat is de lengte van de draad?

Oplossing

Omdat de periode de tijd is die nodig is om een ​​volledige cyclus te maken, waarin deze twee keer door de evenwichtspositie gaat: de ene eerst en de andere terug, dan:

T = 2 × 0.5 s = 1 s

Van:

De lengte L van de draad is gewist:

De thread meet 0.25 m of 25 cm lang.

Referenties

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 2. Dynamisch. Uitgegeven door Douglas Figueroa (USB).
2. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Katz, D. 2013. Natuurkunde voor wetenschappers en ingenieurs. Stichtingen en verbindingen. Cengage leren.
5. Ridder, r.  2017. Fysica voor wetenschappers en engineering: een strategiebenadering.  Pearson.