Montea Triplanar

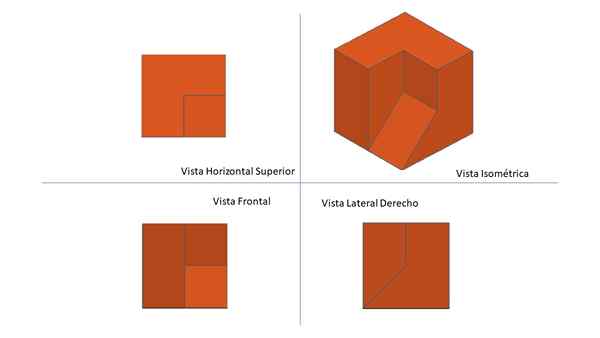
In La Montea Triplanar wordt een drie -dimensionaal stuk weergegeven in een enkel vlak waar de orthogonale projecties van het bovenste horizontale aanzicht, het vooraanzicht en het rechter profielaanzicht worden geplaatst. De volgorde van de getoonde projecties is volgens de ISO-A-standaard. Bron: f. Zapata.

Wat is de Triplanar Mountain?

De Montea Triplanar Het is een manier om een ​​drie -dimensionale figuur in het vlak weer te geven, door de orthogonale projectie van hun gezichten in de Cartesiaanse plannen en alle projecties in een enkel vliegtuig geplaatst.

De beste manier om het projectiesysteem te begrijpen, is om de figuur in een kubisch doos met transparant materiaal voor te stellen. Vervolgens worden de loodrechte projecties van de figuur, op elk van de gezichten van de transparante doos, naar een enkel vlak gebracht.

In La Montea Triplan worden de drie basisprojecties naar een enkel vliegtuig gebracht, die uit de volgende weergaven bestaan:

• Frontaal.
• Bovenste horizontaal.
• Juist profiel.

In het geval van het Amerikaanse systeem ligt het projectievlak tussen de waarnemer en de figuur, maar in het Europese systeem zit het projectievlak achter de figuur, in de waarnemingsrichting. 

Waar is de Triplanar Mountain voor?

De Triplanar Mount dient om drie -dimensionale figuren op een twee -dimensionaal oppervlak weer te geven: het vlak, dat een vel papier of het scherm van een apparaat kan zijn.

Dit vlak is verdeeld in vier kwadranten, die worden gedefinieerd door de kruising van de horizontale en verticale assen. 

De kwadranten worden als volgt vermeld:

• First Quadrant (I): Rechtsboven kwadrant.
• Tweede kwadrant (ii): kwadrant linksboven.
• Derde kwadrant (III): kwadrant linksonder.
• Vierde kwadrant (iv): Quadrant rechtsonder.

Kan u van dienst zijn: Correlatiecoëfficiënt: formules, berekening, interpretatie, voorbeeld

In het geval van het gebruik van het Amerikaanse systeem (ISO-A-standaard) bevinden de projecties zich in de kwadranten volgens de volgende bepaling:

1. De drie -dimensionale figuur in isometrische projectie is in het eerste kwadrant.
2. In het tweede kwadrant wordt het horizontale aanzicht geplaatst (van boven de figuur).
3. De orthogonale projectie van de figuur op het frontale vlak bevindt zich in het derde kwadrant.
4. Ten slotte wordt in het vierde kwadrant het juiste profielaanzicht geplaatst, dat is de projectie van de figuur op een verticaal denkbeeldig vlak, gelegen tussen de figuur en de waarnemer, van het rechterprofiel.

De drie bovengenoemde opvattingen zijn voldoende, omdat het in de meeste gevallen overbodig is om de andere te plaatsen, die zijn:

• Horizontaal lager.
• Linkerkant.
• Achteraanzicht.

Alleen deze weergaven worden gebruikt voor het geval een cijfer die dubbelzinnigheid aanwezig is. Evenzo is het in sommige soorten stukken ook nodig om uitzicht op de transversale of longitudinale sneden ervan te plaatsen, voor duidelijkheid.

Montaa Triplanary Voorbeelden

voorbeeld 1

U wilt de Triplanar Mount bouwen die overeenkomt met een afgeknotte kegel, waarvan de hoofdas parallel is aan het horizontale vlak, volgens de Amerikaanse ISO-A-standaard, ook wel genoemd Derde hoekprojectie.

Omdat het een afgeknotte kegel is met zijn symmetrieas parallel aan het horizontale vlak, wordt de die overeenkomt met het gezicht van de kleinere diameter als een vooraanzicht genomen.

Het vlak waar de spellingsprojectie van elke weergave wordt geplaatst, is verdeeld in vier kwadranten.

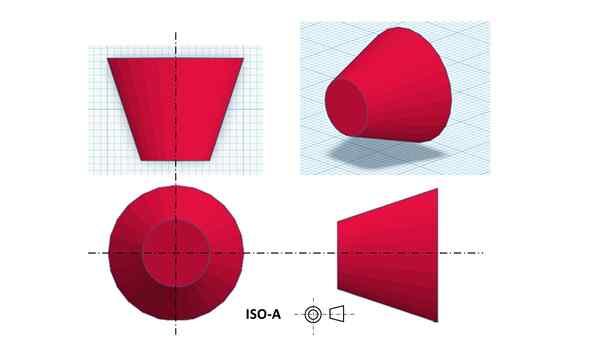Montaa Triplanar de a truncado COO. Bron: f. Zapata

In het Amerikaanse systeem wordt het vooraanzicht in het derde kwadrant geplaatst, daarom staat dit systeem ook bekend als "derde hoek". 

Kan u van dienst zijn: percentage fout

Het horizontale uitzicht van bovenaf is net boven het vooraanzicht geplaatst, dat wil zeggen in het tweede kwadrant.

Ten slotte blijft de projectie, net als in het Amerikaanse systeem, tussen de waarnemer en de figuur, het rechterkantaanzicht bevindt zich precies rechts van het vooraanzicht, dat wil zeggen in het vierde kwadrant.

Omdat het eerste kwadrant gratis was, is er precies het drie -dimensionale isometrische beeld van de figuur, in dit geval de afgeknotte kegel.

In de vorige figuur is het bedrijf of het pictogram dat overeenkomt met de Amerikaanse ISO-A-standaard ook te zien, wat twee concentrische cirkels zijn met een gelijkbenige trapezoid rechts van hen georiënteerd op een zodanige manier dat de korte basis dicht bij de cirkels ligt. Deze oefening verklaart alleen de reden voor dit icoon voor de Amerikaanse norm.

Voorbeeld 2

Het bouwen van de Triplanar Mount die overeenkomt met een afgeknotte kegel waarvan de hoofdas parallel is aan het horizontale vlak, volgens de Europese standaard iso-e, ook wel genoemd Eerste hoekprojectie.

Hiervoor zal de projectie van de afgeknotte kegel van voorbeeld 1 worden gemaakt, maar deze keer met behulp van de Europese of "eerste hoek" -norm.

Evenzo worden het plan waar de verschillende aanzichten of spellingsprojecties van de kegel worden geplaatst, het is verdeeld in vier kwadranten.

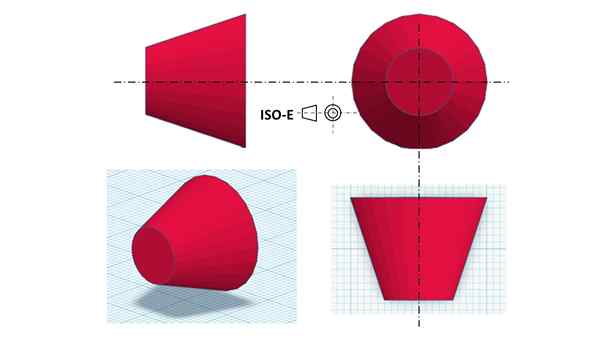Montaa Triplanar de a truncado COO. Bron: f. Zapata.

De eerste is om het vooraanzicht te identificeren, dat de overeenkomst is met het cirkelvormige gezicht met een kleinere diameter van de afgeknotte kegel. Het vooraanzicht ziet eruit als twee concentrische cirkels: een binnenste dat overeenkomt met de kleinste basis van de kegel, en een andere buitenkant die overeenkomt met de hoofdbasis.

Kan u van dienst zijn: prisma's en piramides

In de Europese of "eerste hoek" -conventie bevindt het vooraanzicht zich precies in het eerste kwadrant.

Het bovenste horizontale aanzicht wordt onder het vooraanzicht geplaatst, omdat in het Europese systeem de orthogonale zichtprojectie achter de figuur wordt geplaatst, in de waarnemingsrichting.

Dit betekent dat het bovenaanzicht in het vierde kwadrant wordt geplaatst.

Het zou nodig zijn om de rechterkantaanzicht te vinden, die zich in het Europese systeem links van het vooraanzicht bevindt, in het tweede kwadrant.

Omdat het derde kwadrant gratis is geweest, is het gebruikelijk om de drie -dimensionale isometrische projectie van het stuk te plaatsen.

Dit voorbeeld rechtvaardigt de reden van het zegel, de handtekening of het pictogram van de Europese norm. Dit bestaat uit twee concentrische cirkels die het vooraanzicht van afgeknotte kegel vertegenwoordigen, plus een trapeze dat het rechterkant van hetzelfde vertegenwoordigt, geplaatst aan de linkerkant van de cirkels, met de lange basis naast hen.

Bergtoepassingen Tloplan

De Triplanar Mount wordt toegepast in alle disciplines waar de schaalrepresentatie op een papier of flatscreen van stukken, structuren, gebouwen, drie -dimensionale objecten en andere is vereist.

Dit is de reden waarom deze vorm van representatie die deel uitmaakt van de beschrijvende geometrie een kwestie van studie is in disciplines zoals:

• Machinebouw.
• Metaalmecanische constructies.
• civiele techniek.
• Tekening van sanitaire voorzieningen.
• Architectueel ontwerp.
• Stedelijk ontwerp.
• Topografie.

Om deze reden is La Montea Triplan een verplicht onderzoek in technische scholen en in architectuur- en engineeringcarrières, als onderdeel van onderwerpen zoals beschrijvende geometrie of projectieve geometrie. 

Een vergelijking met studies in brieven en literatuur, waarbij grammatica de basis is om ideeën en gevoelens over te brengen, is projectieve geometrie fundamenteel in engineering en architectuur. Dankzij het is het mogelijk om ideeën te begrijpen, te interpreteren en te interpreteren en te nemen van de plannen tot praktische realisatie.