Schrödinger atomair model

Wat is het atoommodel van Schrödinger?

Hij Schrödinger atomair model Het is een voorstel voor de werking en structuur van het atoom ontwikkeld door Erwin Schrödinger in 1926. Het staat bekend als het kwantummechanische model van het atoom en beschrijft het golfgedrag van het elektron.

Hiervoor was de uitstekende Oostenrijkse natuurkundige gebaseerd op de Broglie -hypothese, die verklaarde dat elk bewegend deeltje wordt geassocieerd met een golf en zich als zodanig kan gedragen.

Erwin Schrödinger

Schrödinger suggereerde dat de beweging van elektronen in het atoom overeenkwam met de dualiteit van de golfdeeltjes, en bijgevolg konden de elektronen rond de kern mobiliseren als stationaire golven.

Schrödinger, die in 1933 de Nobelprijs kreeg voor zijn bijdragen aan Atomic Theory, ontwikkelde de homonieme vergelijking om de kans te berekenen dat een elektron in een specifieke positie zal zijn.

Schrödinger atomaire modelkenmerken

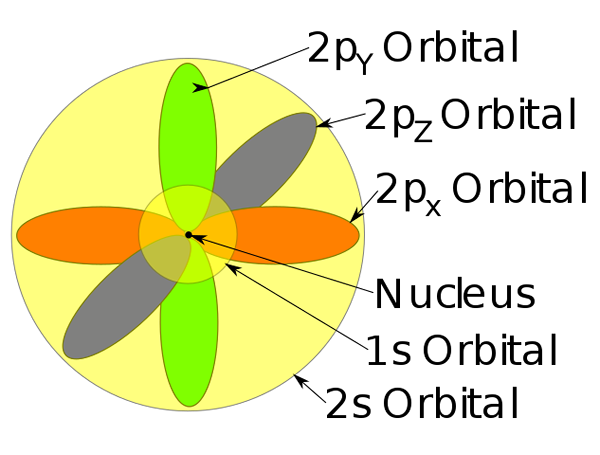Orbitalen 1s, 2s en 2p in een natriumatoom.

-Dit atoommodel beschrijft de beweging van elektronen als stationaire golven.

-De elektronen bewegen constant, dat wil zeggen dat ze geen vaste of gedefinieerde positie binnen het atoom hebben.

-Dit model voorspelt de elektronenlocatie niet, noch beschrijft het de route die het binnen het atoom maakt. Stelt alleen een waarschijnlijkheidszone op om het elektron te vinden.

-Deze waarschijnlijkheidsgebieden worden atomaire orbitalen genoemd. De orbitalen beschrijven een vertaalbeweging rond de kern van het atoom.

-Deze atomaire orbitalen hebben verschillende niveaus en energieniveau en kunnen worden gedefinieerd tussen elektronenwolken.

-Het model overweegt niet de stabiliteit van de kern, het verwijst alleen om de kwantummechanica te verklaren die verband houdt met de beweging van elektronen in de atoom.

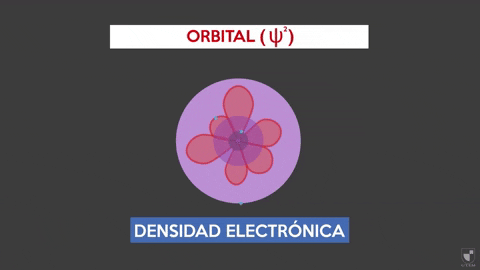Elektronische dichtheid geeft de kans op het vinden van een elektron in de buurt van de kern. Hoe dichter de kern (paarse zone) er meer waarschijnlijkheid zal zijn, terwijl het minder zal zijn als u weggaat van de kern (Violet Area).

Experiment

Het atoommodel van Schrödinger is gebaseerd op de Broglie -hypothese, evenals de vorige atoommodellen van Bohr en Sommerfeld. 

Kan u van dienst zijn: dynamische of kinetische wrijving: coëfficiënt, voorbeelden, oefeningen

Broglie stelde voor dat net zoals golven deeltjes hebben, deeltjes golfeigenschappen hebben, met een bijbehorende golflengte. Iets dat destijds veel verwachting heeft gegenereerd, albert Einstein zelf op zijn theorie.

Broglie's theorie had echter een gebrek, namelijk dat de betekenis van een eigen idee niet zo goed werd begrepen: een elektron kan een golf zijn, maar hoe zit het met wat? Dat is wanneer de figuur van Schrödinger lijkt te antwoorden.

Om dit te doen, vertrouwde de Oostenrijkse natuurkundige op het experiment van Young en op basis van zijn eigen observaties ontwikkelde hij de wiskundige uitdrukking die zijn naam draagt.

Vervolgens de wetenschappelijke grondslagen van dit atoommodel:

Young's experiment: de eerste demonstratie van dualiteit van golfdeeltjes

Broglie's hypothese over het golvende en corpusculaire karakter van het onderwerp kan worden aangetoond door het experiment van Young, ook bekend als Double Slit Experiment.

De Engelse wetenschapper Thomas Young legde de basis van het atoommodel van Schrödinger toen hij in 1801 het experiment uitvoerde om de golvende aard van het licht te verifiëren.

Tijdens zijn experimenten verdeelde Young de emissie van een lichtstraal dat een klein gat door een observatiekamer kruist. Deze divisie wordt bereikt met behulp van een kaart van 0,2 millimeter, parallel aan de balk gelegen.

Het ontwerp van het experiment werd gemaakt om de lichtstraal breder te zijn dan de kaart, waardoor de kaart horizontaal werd geplaatst, werd de balk verdeeld in ongeveer dezelfde delen. De uitgang van de lichtstralen werd geregisseerd door een spiegel.

Kan je van dienst zijn: afstandskrachten

Beide lichtstralen raken een muur in een donkere kamer. Daar werd het interferentiepatroon tussen de twee golven aangetoond, die werd aangetoond dat het licht net zoveel kon gedragen als een deeltje en een golf.

Een eeuw later versterkte Albert Einsten het idee door de principes van de kwantummechanica.

Schrödinger's vergelijking

Schrödinger ontwikkelde twee wiskundige modellen, onderscheiden wat er gebeurt, afhankelijk van of de kwantumstaat in de loop van de tijd verandert of niet.

Voor atomaire analyse publiceerde Schrödinger in de late 1926.

Dit houdt in dat de golf niet beweegt, zijn knooppunten, dat wil zeggen, zijn evenwichtspunten, dienen als een draaipunt voor de rest van de structuur om er omheen te bewegen en een bepaalde frequentie en amplitude te beschrijven.

Schrödinger definieerde de golven die elektronen beschrijven als stationaire of orbitale toestanden, en worden op hun beurt geassocieerd op verschillende niveaus van energie.

Schrödinger's onafhankelijke tijdvergelijking is als volgt:

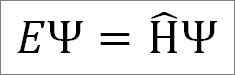
Waar:

EN: Evenredigheid constant.

Ψ: Golffunctie van kwantumsystemen.

Η ̂: Hamiltoniaanse operator.

De onafhankelijke tijdvergelijking van de Schrödinger wordt gebruikt wanneer de waarneembare die de totale energie van het systeem vertegenwoordigt, bekend als Hamiltoniaanse operator, hangt niet af van de tijd. De functie die beschrijft aan de totale golfbeweging zal echter altijd afhangen van de tijd.

De vergelijking van Schrödinger geeft aan dat als u een golffunctie ψ hebt, en de Hamiltoniaanse operator erop werkt, de evenredigheidsconstante en de totale energie van het kwantumsysteem vertegenwoordigt in een van de stationaire toestanden.

Het kan u van dienst zijn: discrete variabele: kenmerken en voorbeelden

Toegepast op het atoommodel van Schrödinger, als het elektron in een gedefinieerde ruimte beweegt, zijn er discrete energiewaarden, en als het elektron vrij wordt verschoven in de ruimte, worden continue energie -intervallen verkregen.

Vanuit wiskundig oogpunt zijn er verschillende oplossingen voor de Schrödinger -vergelijking, elke oplossing impliceert een andere waarde voor de evenredigheidsconstante en.

Volgens het onzekerheidsprincipe van Heisenberg is het niet mogelijk om de positie of energie van een elektron te schatten. Bijgevolg erkennen wetenschappers dat de schatting van de elektronenlocatie binnen het atoom onnauwkeurig is.

Postulaten van het Schrödinger -atoommodel

De postulaten van het Schrödinger -atoommodel zijn de volgende:

-De elektronen gedragen zich als stationaire golven die in de ruimte zijn verdeeld volgens de golffunctie ψ.

-De elektronen bewegen in het atoom dat orbitalen beschrijft. Dit zijn gebieden waar de kans op het vinden van een elektron aanzienlijk hoger is. De bovengenoemde waarschijnlijkheid is evenredig met het kwadraat van de golffunctie ψ².

De elektronische configuratie van het Schrödinguer -atoommodel verklaart de periodieke eigenschappen van atomen en links die vormen.

Het atoommodel van Schrödinger overwegen echter niet de spin van elektronen en houdt geen rekening met de variaties van snelle elektronen als gevolg van relativistische effecten als gevolg van relativistische effecten.

Interessante artikelen

Broglie Atomic Model.

Chadwick Atomic Model.

Heisenberg Atomic Model.

Perrin Atomic Model.

Thomson Atomic Model.

Dalton Atomic Model.

Dirac Jordan Atomic Model.

Democritus Atomic Model.

Leucipo -atoommodel.

Bohr Atomic Model.

Sommend Atomic Model.

Huidig ​​atoommodel.

Referenties

1. Het kwantummechanische model van het atoom hersteld uit: het is.Khanacademy.borg
2. Schrödinger's golfvergelijking (s.F.)). Jaime I University. Castellón, Spanje. Hersteld van: uji.is
3. Moderne atoomtheorie: modellen. © ABCTE. Hersteld van: abcte.borg
4. Schrodinger's Atomic Mod.F.)). Hersteld van: ErwinschrodingerBiography.Weebel.com
5. Wikipedia, gratis encyclopedie. Schrödinger -vergelijking. Hersteld van: is.Wikipedia.borg
6. Wikipedia, gratis encyclopedie. Jong experiment. Hersteld van: is.Wikipedia.borg