Inverse matrixberekening en oefening zijn opgelost

De Omgekeerde matrix Van een gegeven matrix is ​​het de matrix die vermenigvuldigd is met de oorspronkelijke resultaten in de identiteitsmatrix. De omgekeerde matrix is ​​nuttig voor het oplossen van systemen van lineaire vergelijkingen, vandaar het belang van weten hoe deze te berekenen.

De matrices zijn erg nuttig in de natuurkunde, engineering en wiskunde, omdat ze een compact hulpmiddel zijn om complexe problemen op te lossen. Het nut van matrices wordt verbeterd wanneer ze omkeerbaar zijn en ook hun omgekeerde is bekend.

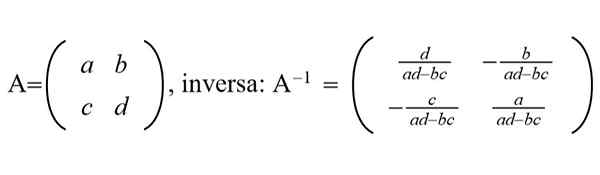Figuur 1. Een generieke 2 × 2 -matrix en de inverse matrix worden getoond. (Opgesteld door Ricardo Pérez)

In de grafische verwerkingsvelden worden big data, datamining, machine learning en andere efficiënte en snelle algoritmen gebruikt om de NXN -matrices inverse matrix met n zeer groot te evalueren, in de volgorde van de duizenden of miljoenen.

Om het gebruik van de omgekeerde matrix te illustreren bij het beheer van het systeem van lineaire vergelijkingen zullen we beginnen met het eenvoudigste geval van alle: 1 × 1 matrices.

Het eenvoudigste geval: een lineaire vergelijking van een enkele variabele wordt overwogen: 2 x = 10.

Het idee is om de waarde van X te vinden, maar het zal "matrixly" zijn. 

De matrix m = (2) die de vector (x) vermenigvuldigt, is een 1 × 1 -matrix die resulteert in de vector (10):

M (x) = (10)

De omgekeerde van de M -matrix wordt aangeduid door M^-1.

De algemene manier om dit "lineaire systeem" te schrijven is:

M x = b, waarbij x de vector (x) is en b de vector is (10).

Per definitie is de omgekeerde matrix er een die vermenigvuldigd is met de oorspronkelijke matrix resulteert in de identiteitsmatrix I:

M^-1 M = i

In het geval dat wordt overwogen, matrix m^-1 Het is de matrix (½), dat is m^-1 = (½) sinds m^-1 M = (½) (2) = (1) = i

Kan u van dienst zijn: 90 divisors: wat zijn en uitleg

Om de onbekende vector x = (x) te vinden, worden beide leden in de verhoogde vergelijking vermenigvuldigd met de omgekeerde matrix:

M^-1 M (x) = m^-1 (10)

(½) (2) (x) = (½) (10)

(½ 2) (x) = (½ 10)

(1) (x) = (5)

(x) = (5)

Gelijkheid van twee vectoren is bereikt, die alleen hetzelfde zijn als hun overeenkomstige elementen gelijk zijn, dat wil zeggen x = 5.

Berekening van de inverse van een matrix

Wat de berekening van de omgekeerde matrix motiveert, is het vinden van een universele methode voor de oplossing van lineaire systemen zoals het volgende 2 × 2 -systeem:

x - 2 y = 3

-x + y = -2

Na de stappen van case 1 × 1, bestudeerd in de vorige sectie, schrijven we het systeem van vergelijkingen op een matrix manier:

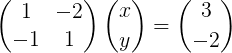Figuur 2. Lineair systeem in matrixvorm.

Merk op dat dit systeem als volgt in compacte vectornotatie is geschreven:

M x = B

waar

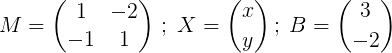
De volgende stap is om m te vinden.

Methode 1: door Gaussiaanse eliminatie

De Gauss -eliminatiemethode wordt toegepast. Die bestaat uit het uitvoeren van elementaire bewerkingen op de gelederen van de matrix, deze bewerkingen zijn:

- Vermenigvuldig een rij met een niet -nulnummer.

- Een andere rij of het veelvoud van een andere rij toevoegen of aftrekken.

- Rijs wisselen.

Het doel is, via deze bewerkingen, om de originele matrix om te zetten in de identiteitsmatrix. 

Zoals dit wordt gedaan, worden in matrix M exact dezelfde bewerkingen op de identiteitsmatrix toegepast. Wanneer het na verschillende bewerkingen in de R -rijen wordt getransformeerd naar de unitaire matrix, dan wordt degene die oorspronkelijk de eenheid was omgezet in de omgekeerde matrix van M, dat wil zeggen m^-1.

Kan u van dienst zijn: Corollary (geometrie)

1- We beginnen het proces door de matrix M te schrijven en ernaast de eenheidsmatrix:

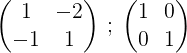
2- We voegen de twee rijen toe en het resultaat wordt op de tweede rij geplaatst, op deze manier krijgen we een nul in het eerste element van de tweede rij:

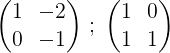
3- We vermenigvuldigen de tweede rij met -1 om 0 en 1 op de tweede rij te verkrijgen:

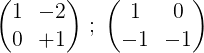
4- De eerste rij wordt vermenigvuldigd met ½:

5- De tweede en de eerste voegt eraan toe en het resultaat wordt op de eerste rij geplaatst:

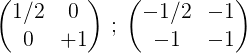
6- Om het proces te beëindigen, wordt de eerste rij met 2 vermenigvuldigd om in de eerste de identiteitsmatrix te verkrijgen en in de tweede de omgekeerde matrix van de oorspronkelijke matrix M:

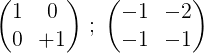
Het is te zeggen:

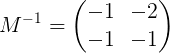
Systeemoplossing

Zodra de omgekeerde matrix is ​​verkregen, wordt het systeem van vergelijkingen opgelost door de omgekeerde matrix toe te passen in beide leden van de compacte vectorvergelijking:

M^-1M x = m^-1B

X = m^-1B

Dat blijft expliciet zo:

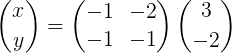
Vervolgens wordt de matrixvermenigvuldiging gemaakt om vector X te verkrijgen:

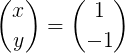
Methode 2: door bijgevoegde matrix

In deze tweede methode wordt de omgekeerde matrix berekend op basis van de bijgevoegde matrix van de originele matrix NAAR.

Stel dat een matrix wordt gegeven door:

waarheen_{ik, j} Het is het element van de rij Je en de kolom J van de matrix NAAR.

De bevestiging van de matrix NAAR Het zal worden gebeld Adj (a) En de elementen zijn:

ADVERTENTIE_{ik, j} = (-1)^(I+J) ¦ai, j¦

waar Ai, j Het is de complementaire kleine matrix die wordt verkregen door rij I en kolom J uit de originele matrix te elimineren NAAR. Staven ¦ ¦ geven aan dat de determinant is berekend, dat wil zeggen ¦ai, j¦ Het is de bepalende factor van de complementaire kleine matrix.

Kan u van dienst zijn: homologe kanten

Inverse matrixformule

De formule om de omgekeerde matrix te vinden op basis van de bijgevoegde matrix van de oorspronkelijke matrix is ​​als volgt:

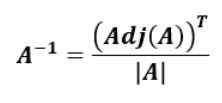
Dat wil zeggen de omgekeerde matrix van NAAR, NAAR^-1, is het transponeren van de bevestiging van NAAR gedeeld door de determinant van NAAR.

De omgezet NAAR^Tvan een matrix NAAR Het is degene die is verkregen door rangen uit te wisselen voor kolommen, dat wil zeggen dat de eerste rij de eerste kolom en de tweede rij naar de tweede kolom wordt, enzovoort tot de N -rijen van de originele matrix.

Oefening opgelost

Wees de matrix van de volgende:

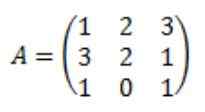
Elk van de elementen van de bijgevoegde matrix van A: adj (a) worden berekend

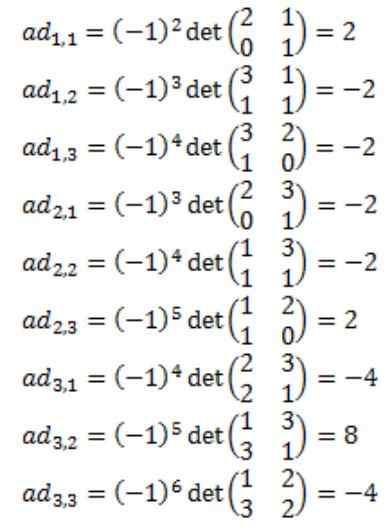
Als gevolg dat de bijgevoegde matrix van A, adj (a) als volgt is:

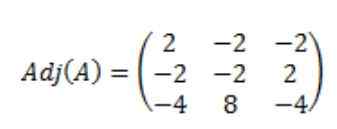
Vervolgens wordt de bepalende factor van matrix a, det (a) berekend:

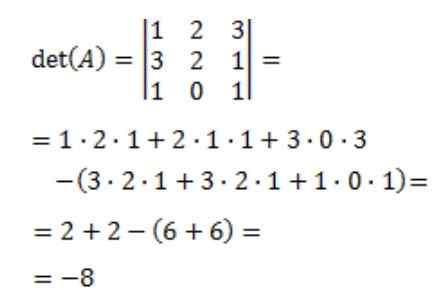
Ten slotte wordt de omgekeerde matrix van A verkregen:

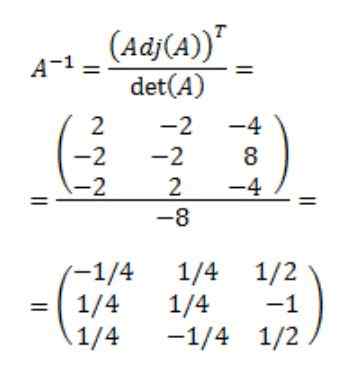
Referenties

1. Anthony Nicolaides (1994) Determinanten en matrices. Pass Publicatie.
2. Awol Assen (2013) Een onderzoek naar de berekening van de determinanten van 3 × 3
3. Casteleiro Villalba M. (2004) Inleiding tot lineaire algebra. ESIC -redactie.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
6. Richard J. Brown (2012) 30-seconden wiskunde: de 50 meest geestverruimende theorieën in wiskunde. Ivy Press Limited.
7. Matrix. Lap Lambert Academic Publishing.