Klassenmerk

Wat is een klassenmerk?

De Klassenmerk, Ook bekend als het middelpunt, het is de waarde die zich in het midden van een klasse bevindt, die alle waarden vertegenwoordigt die in die categorie staan. Fundamenteel wordt het klassenmerk gebruikt voor de berekening van bepaalde parameters, zoals rekenkundig gemiddelde of standaardafwijking.

Dan is het klassenmerk het middelpunt van elk interval. Deze waarde is ook erg handig om de variantie van een gegevensset te vinden die al in CLAS is gegroepeerd.

Frequentieverdeling

Om te begrijpen wat een klassenmerk nodig is, het concept van frequentieverdeling. Gezien een gegevensset is een frequentieverdeling een tabel die deze gegevens verdeelt in een aantal categorieën die klassen worden genoemd.

Deze tabel laat zien wat de hoeveelheid elementen is die bij elke klasse behoren; De laatste staat bekend als frequentie.

In deze tabel wordt een deel van de informatie die we verkrijgen uit de gegevens opgeofferd, omdat we in plaats van de individuele waarde van elk element hebben, alleen weten dat deze bij deze klasse hoort.

Aan de andere kant krijgen we een beter begrip van de gegevensset, omdat het op deze manier gemakkelijker is om gevestigde patronen te waarderen, die de manipulatie van genoemde gegevens vergemakkelijkt.

Hoeveel klassen overwegen?

Om een ​​frequentieverdeling te maken, moeten we eerst het aantal klassen bepalen dat u wilt volgen en de klassenlimieten van hetzelfde kiezen.

Kan u van dienst zijn: randen van een kubus

De keuze van hoeveel klassen moeten handig zijn, rekening houdend met dat een klein aantal klassen informatie kan verbergen over de gegevens die we willen bestuderen en een zeer grote kan te veel details genereren die niet noodzakelijk nuttig zijn.

De factoren waarmee we rekening moeten houden bij het kiezen van hoeveel klassen meerdere zijn, maar tussen deze zijn twee: de eerste is om rekening te houden met hoeveel gegevens we moeten overwegen; De tweede is om te weten welke grootte van het distributiebereik is (dat wil zeggen het verschil tussen de grootste en kleinste observatie).

Na het hebben van de reeds gedefinieerde klassen tellen we door tot het tellen hoeveel gegevens in elke klasse. Dit nummer wordt klassenfrequentie genoemd en wordt per fix aangeduid.

Zoals we eerder hadden gezegd, hebben we een frequentieverdeling verliest de informatie die individueel uit elke gegevens of observatie komt. Daarom wordt een waarde gezocht die de hele klasse vertegenwoordigt waartoe hij behoort; Deze waarde is de classmark.

Hoe wordt het verkregen?

Het klassenmerk is de centrale waarde die een klasse vertegenwoordigt. Het wordt verkregen door de limieten van het interval toe te voegen en deze waarde door twee te verdelen. We zouden dit wiskundig als volgt kunnen uiten:

X_Je= (Ondergrens + bovengrens)/2.

In deze uitdrukking x_Je Geeft het merk van de I-deze klasse aan.

Voorbeeld

Gezien de volgende gegevensset, geef een representatieve frequentieverdeling en krijg de bijbehorende klassenmerk.

Aangezien de gegevens met de hoogste numerieke waarde 391 zijn en het kind 221 is, hebben we dat het bereik 391 -221 = 170 is.

Kan u van dienst zijn: theoretische waarschijnlijkheid: hoe u het uit kunt krijgen, voorbeelden, oefeningen

We zullen 5 klassen kiezen, allemaal met dezelfde maat. Een manier om klassen te kiezen is als volgt:

Merk op dat elke gegevens zich in een klasse bevinden, deze zijn disjunct en hebben dezelfde waarde. Een andere manier om klassen te kiezen, is het overwegen van gegevens als onderdeel van een continue variabele, die elke reële waarde kan bereiken. In dit geval kunnen we klassen van de vorm overwegen:

205-245, 245-285, 285-325, 325-365, 365-405

Deze manier om de gegevens te groeperen kan echter bepaalde dubbelzinnigheden met de grenzen presenteren. Bijvoorbeeld, in het geval van 245 rijst de vraag: tot welke klasse behoort het tot de eerste of de tweede?

Om deze verwarring te voorkomen, wordt een conventie van extreme punten gemaakt. Op deze manier zal de eerste klasse het interval zijn (205,245], de tweede (245,285], enzovoort.

Nadat de klassen zijn gedefinieerd, gaan we verder met het berekenen van de frequentie en hebben we de volgende tabel:

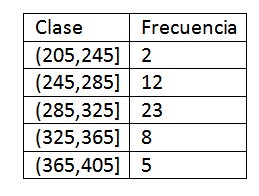
Na het verkrijgen van de frequentieverdeling van de gegevens, gaan we verder met het vinden van de klassenmerken van elk interval. Inderdaad, we moeten:

X₁= (205+ 245)/2 = 225

X₂= (245+ 285)/2 = 265          

X₃= (285+ 325)/2 = 305

X₄= (325+ 365)/2 = 345

X₅= (365+ 405)/2 = 385

We kunnen dit weergeven via de volgende grafiek:

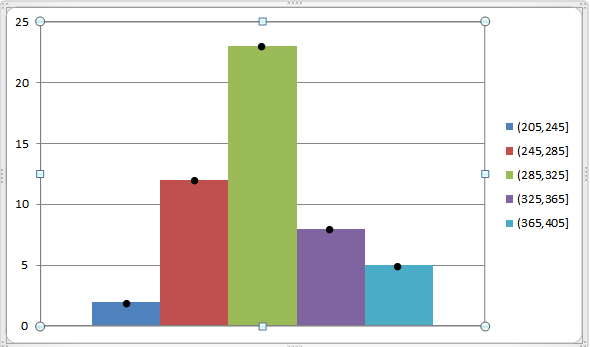
Waar is het voor?

Het klassenmerk is zeer functioneel om het rekenkundige gemiddelde te vinden en de variantie van een datagroep die al in verschillende klassen is gegroepeerd.

We kunnen het rekenkundig gemiddelde definiëren als de som van de waarnemingen die zijn verkregen tussen de steekproefgrootte. Vanuit fysiek oogpunt is de interpretatie ervan als het balanspunt van een gegevensset.

Het identificeren van een hele set gegevens met één nummer kan riskant zijn, dus u moet ook rekening houden met het verschil tussen dit evenwichtspunt en de echte gegevens. Deze waarden staan ​​bekend als afwijking van het rekenkundig gemiddelde, en daarmee wordt gezocht om te bepalen hoeveel het rekenkundige gemiddelde van de gegevens varieert.

Kan u van dienst zijn: breuken: typen, voorbeelden, oefeningen opgelost

De meest voorkomende manier om deze waarde te vinden is vanwege de variantie, die het gemiddelde is van de vierkanten van de afwijkingen van het rekenkundig gemiddelde.

Om het rekenkundig gemiddelde en de variantie van een set gegevens te berekenen die zijn gegroepeerd in een klasse, gebruiken we respectievelijk de volgende formules:

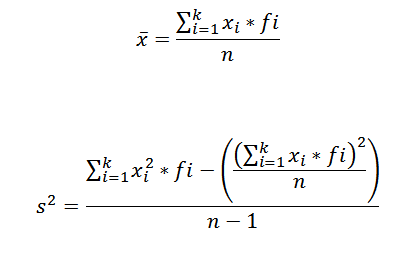
In deze uitdrukkingen x_Je  Het is het I-This Class-merk, f_Je vertegenwoordigt de overeenkomstige frequentie en k Het aantal klassen waarin de gegevens zijn gegroepeerd.

Voorbeeld

Gebruikmakend van de gegevens die in het vorige voorbeeld worden gegeven, moeten we de gegevens in de frequentiedistributietabel iets meer uitbreiden. Het volgende wordt verkregen:

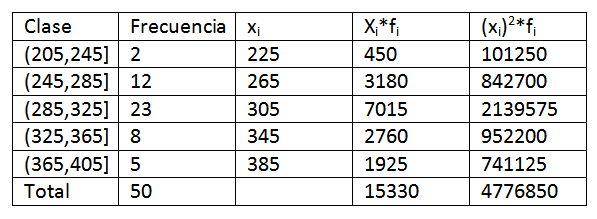
Door de gegevens in de formule te vervangen, hebben we dan achtergelaten dat het rekenkundige gemiddelde is:

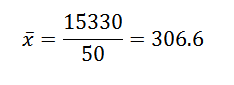
De variantie en standaardafwijking zijn:

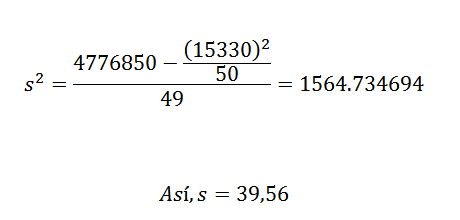
Hieruit kunnen we concluderen dat de oorspronkelijke gegevens een rekenkundig gemiddelde hebben van 306.6 en een standaardafwijking van 39.56.