Vectoralgebra

Wat is de vectoralgebra?

Hij Vectoralgebra Het is een tak van wiskunde die verantwoordelijk is voor het bestuderen van systemen van lineaire vergelijkingen, vectoren, matrices, vectorruimtes en hun lineaire transformaties. Het is gerelateerd aan gebieden zoals engineering, resolutie van differentiaalvergelijkingen, functionele analyse, operationele onderzoek, computationele grafische afbeeldingen, onder andere.

Een andere van de gebieden die de lineaire algebra heeft aangenomen, is fysica, omdat het hierdoor mogelijk is geweest om de studie van fysieke fenomenen te ontwikkelen, waardoor ze worden beschreven door het gebruik van vectoren. Dit heeft een beter begrip van het universum mogelijk gemaakt.

Fundamentals

De vectoralgebra is afkomstig van de studie van de quaternions (uitbreiding van de reële getallen) 1, i, j en k, evenals de Cartesiaanse geometrie gepromoot door Gibbs en Heaviside, die zich realiseerden dat de vectoren zouden dienen als een instrument voor vertegenwoordigen Verschillende fysieke fenomenen.

De vectoralgebra wordt bestudeerd via drie stichtingen:

Geometrisch

Vectoren worden weergegeven door lijnen die een oriëntatie hebben, en bewerkingen zoals som, aftrekking en vermenigvuldiging door reële getallen worden gedefinieerd door middel van geometrische methoden.

Analytisch

De beschrijving van de vectoren en hun bewerkingen wordt uitgevoerd met getallen, componenten genoemd. Dit type beschrijving is het resultaat van een geometrische weergave omdat een coördinatensysteem wordt gebruikt.

Axiomatisch

Een beschrijving van de vectoren wordt gemaakt, ongeacht het coördinatensysteem of van enig type geometrische weergave.

De studie van cijfers in de ruimte wordt gedaan door zijn weergave in een referentiesysteem, dat in een of meer dimensies kan zijn. Onder de belangrijkste systemen zijn:

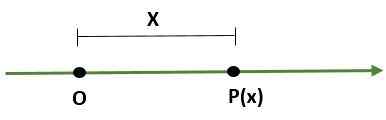
• Unidimensionaal systeem, dat het een lijn is waar een punt (OR) de oorsprong vertegenwoordigt en een ander punt (P) de schaal (lengte) en de richting hiervan bepaalt:

• Rechthoekig coördinatensysteem (twee -dimensionaal), dat is samengesteld uit twee loodrechte lijnen genaamd X- en Y -as, die door een punt (of) oorsprong gaan; Op deze manier is het plan verdeeld in vier regio's die kwadranten worden genoemd. In dit geval wordt een punt (P) in het vlak gegeven door de afstanden die bestaan ​​tussen de assen en P.

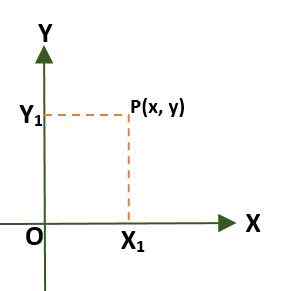
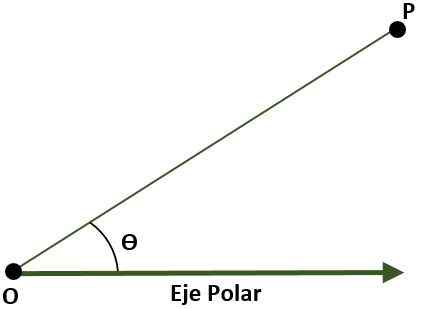
• Polair coördinatensysteem (twee -dimensionaal). In dit geval is het systeem samengesteld uit een punt O (oorsprong) die pool wordt genoemd en een semi -river met oorsprong in of een polaire as genoemd. In dit geval wordt het punt P van het vlak, met verwijzing naar de pool en de polaire as, gegeven door de hoek (ɵ), die wordt gevormd door de afstand tussen de oorsprong en het punt P.

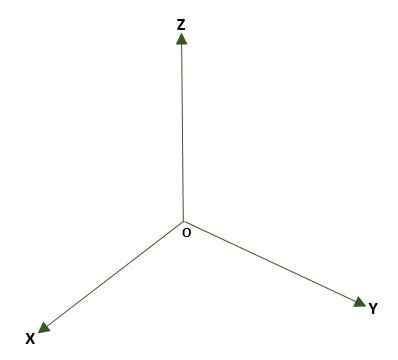
• Rechthoekig drie -dimensionaal systeem, gevormd door drie loodrechte lijnen (x, y, z) die zijn punt of in de ruimte hebben. Drie coördinaatvliegtuigen worden gevormd: XY, XZ en YZ; De ruimte zal worden onderverdeeld in acht regio's genaamd Octants. De referentie van een punt P van de ruimte wordt gegeven door de afstanden die bestaan ​​tussen de vlakken en P.

Grootte

Een grootte is een fysieke hoeveelheid die kan worden geteld of gemeten door een numerieke waarde, zoals in het geval van enkele fysische fenomenen; Het is echter vaak noodzakelijk om deze fenomenen te beschrijven met andere factoren die niet numeriek zijn. Dat is de reden waarom de magnitudes worden ingedeeld in twee soorten:

Scalaire omvang

Het zijn die bedragen die zijn gedefinieerd en op een numerieke manier vertegenwoordigen; dat wil zeggen, door een module samen met een meeteenheid. Bijvoorbeeld:

a) tijd: 5 seconden.

b) Massa: 10 kg.

c) Volume: 40 ml.

D) Temperatuur: 40 ºC.

Vectorgrootte

Het zijn die hoeveelheden die worden gedefinieerd en vertegenwoordigd door een module samen met een eenheid, evenals door een zin en richting. Bijvoorbeeld:

Kan u van dienst zijn: symbolisatie van uitdrukkingen

A) Snelheid: (5ȋ - 3ĵ) M/s.

b) Versnelling: 13 m /s²; S 45º E.

c) kracht: 280 N, 120º.

d) Gewicht: -40 ĵ kg -f.

Vectorgroottes worden grafisch weergegeven door vectoren.

Wat zijn vectoren?

Vectoren zijn grafische representaties van een vectorgrootte; dat wil zeggen, het zijn lijnsegmenten waarin het laatste einde de top van een pijl is.

Deze worden bepaald door zijn module of lengte van het segment, hun gevoel dat wordt aangegeven door de punt van zijn pijl en zijn richting volgens de lijn waartoe het behoort. De oorsprong van een vector staat ook bekend als het toepassingspunt.

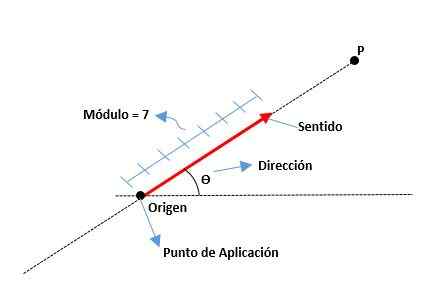
De elementen van een vector zijn de volgende:

Module

Het is de afstand van de oorsprong tot het einde van een vector, vertegenwoordigd door een reëel getal samen met een eenheid. Bijvoorbeeld:

| OM | = | A | = A = 6 cm

Adres

Het is de maat van de hoek die bestaat tussen de X -as (van het positieve) en de vector, evenals de kardinale punten (noord, zuid, oost en west) worden ook gebruikt.

Gevoel

Het wordt gegeven door de pijlpunt aan het einde van de vector, wat aangeeft waar dit is gericht.

Classificatie van vectoren

Over het algemeen worden vectoren geclassificeerd als:

Vaste vector

Het is degene wiens applicatiepunt (oorsprong) is vastgesteld; dat wil zeggen, het blijft gekoppeld aan een ruimte van ruimte, dus het kan hier niet in bewegen.

Gratis vector

Het kan vrij in de ruimte bewegen omdat de oorsprong ervan naar elk punt beweegt zonder de module, betekenis of richting te wijzigen.

Schuifvector

Het is er een die zijn oorsprong kan overdragen langs zijn werklijn zonder de module, betekenis of richting te wijzigen.

Vector -eigenschappen

Onder de belangrijkste eigenschappen van de vectoren zijn de volgende:

Equipoire vectoren

Het zijn die vrije vectoren met dezelfde module, richting (of deze zijn parallel) en zintuigen als een schuifvector of een vaste vector.

Gelijkwaardige vectoren

Het treedt op wanneer twee vectoren hetzelfde adres hebben (of parallel) zijn, dezelfde zin, en ondanks het feit dat ze verschillende modules en toepassingspunten hebben, veroorzaken ze gelijke effecten.

Vector -gelijkheid

Deze hebben dezelfde module, richting en zin, zelfs wanneer hun uitgangspunten anders zijn, waardoor een parallelle vector naar zichzelf kan gaan zonder dit te beïnvloeden.

Tegenovergestelde vectoren

Zij zijn degenen die dezelfde module en richting hebben, maar hun betekenis is tegenover.

Eenheidsvector

Het is er een waarin de module gelijk is aan eenheid (1). Dit wordt verkregen door de vector te verdelen door de module en wordt gebruikt om de richting en richting van een vector, hetzij in het vlak of in de ruimte, te bepalen met behulp van de gestandaardiseerde basis- of eenheidsvectoren, die:

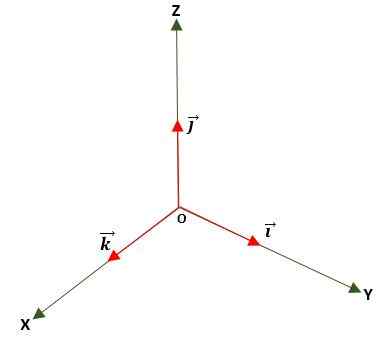
Nulvector

Het is degene wiens module gelijk is aan 0; dat wil zeggen, het punt van oorsprong en extreem valt op hetzelfde punt samen.

Vectorcomponenten

De componenten van een vector zijn die waarden van de vectorprojecties op de assen van het referentiesysteem; Afhankelijk van de ontleding van de vector, die in assen van twee of drie dimensies kunnen zijn, worden respectievelijk twee of drie componenten verkregen.

De componenten van een vector zijn reële getallen, die positief, negatief of zelfs nul kunnen zijn (0).

Op deze manier, als u een ā -vector heeft, afkomstig uit een rechthoekig coördinatensysteem in het XY (twee -dimensionale) vlak, is de projectie op de x -as āx en de projectie op de y -as en is āy. Aldus zal de vector worden uitgedrukt als de som van zijn componentvectoren.

Voorbeelden

Eerste voorbeeld

Je hebt een ā vector die begint bij de oorsprong en coördinaten van de uiteinden worden gegeven. Dus de vector ā = (ā_X; NAAR_En) = (4; 5) cm.

Kan u van dienst zijn: 120 delers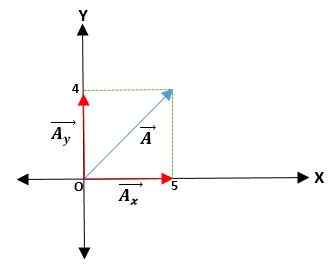

Als de vector ā werkt op de oorsprong van een drie -dimensionaal driehoekig coördinatensysteem (in de ruimte) x, y, z, naar een ander punt (p), zullen de projecties op hun bijlen āx, āy en āz zijn; De vector zal dus worden uitgedrukt als de som van zijn drie componentvectoren.

Tweede voorbeeld

Je hebt een ā vector die begint bij de oorsprong en coördinaten van de uiteinden worden gegeven. Dus de vector ā = (a_X; NAAR_En; NAAR_Z) = (4; 6; -3) cm.

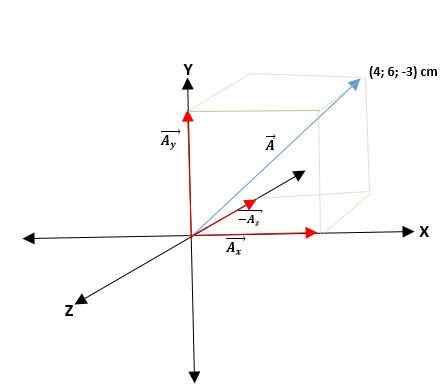
Vectoren die hun rechthoekige coördinaten hebben, kunnen worden uitgedrukt volgens hun basisvectoren. Daarvoor moet alleen elke coördinaat worden vermenigvuldigd met de respectieve eenheidsvector, zodat ze voor het vlak en de ruimte de volgende zullen zijn:

Voor het vliegtuig: ā = a_Xi +a_EnJ.

Voor ruimte: ā = a_Xi +a_EnJ+A_Zk.

Bewerkingen met vectoren

Er zijn veel magnitudes met module, betekenis en richting, zoals versnelling, snelheid, verplaatsing, kracht, onder anderen.

Deze worden toegepast op verschillende wetenschappelijke gebieden, en om ze toe te passen, is het in sommige gevallen noodzakelijk om operaties uit te voeren zoals som, aftrekking, vermenigvuldiging en verdeling van vectoren en scalars.

Toevoeging en aftrekking van vectoren

De som en aftrekking van vectoren wordt beschouwd als een enkele algebraïsche bewerking omdat aftrekking als een som kan worden geschreven; De aftrekking van vectoren ā en ē kan bijvoorbeeld worden uitgedrukt als:

Ā - ē = ā + (-ē)

Er zijn verschillende methoden om de som en aftrekking van vectoren uit te voeren: ze kunnen afbeeldingen of analyses zijn.

Grafische methoden

Gebruikt wanneer een vector een module, gevoel en richting heeft. Hiervoor worden lijnen getekend die een figuur vormen die vervolgens helpt bij het bepalen van het resultaat. Een van de bekendste zijn de volgende:

Parallellogrammethode

Om de som of aftrekking van twee vectoren te maken, wordt een gemeenschappelijk punt gekozen op de coördinaatas -die het punt van oorsprong van de vectoren weergeeft -, het handhaven van hun module, richting en richting.

Vervolgens worden parallelle lijnen getrokken naar de vectoren om een ​​parallellogram te vormen. De resulterende vector is de diagonaal die vertrekt van het punt van oorsprong van beide vectoren naar het hoekpunt van het parallellogram:

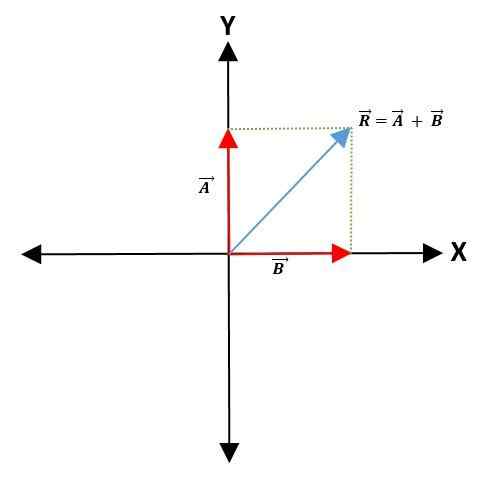
Driehoeksmethode

In deze methode worden de vectoren onder de andere geplaatst, waarbij hun modules, zintuigen en adressen worden gehandhaafd. De resulterende vector zal de unie zijn van de oorsprong van de eerste vector met het einde van de tweede vector:

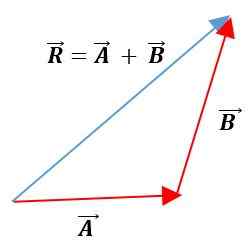
analytische methodes

Twee of meer vectoren kunnen worden toegevoegd of afgetrokken via een geometrische of vectormethode:

Geometrische methode

Wanneer twee vectoren een driehoek of parallellogram vormen, kunnen de M [odulo en de richting van de resulterende vector worden bepaald met behulp van de wetten van de borst en cosinus. Aldus wordt de resulterende vectormodule, die de wet van de cosinus en de driehoeksmethode toepast, gegeven door:

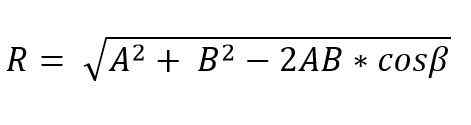
In deze formule is β de tegenovergestelde hoek ten opzichte van de R -zijde, en dit is gelijk aan 180º - ɵ.

Aan de andere kant is de resulterende vectormodule volgens de parallellogrammethode:

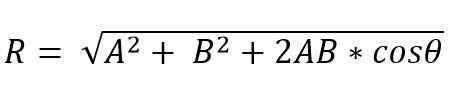
Het resulterende vectoradres wordt gegeven door hoek (α), die de resulterende vormt met een van de vectoren.

Door de borstwetgeving kan de som of aftrekking van vectoren ook worden gedaan door de driehoek- of parallellogrammethode, wetende dat in elke driehoek de zijkanten evenredig zijn met de borsten van de knappe hoeken:

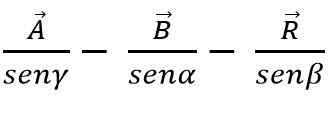
Vectormethode

Dit kan op twee manieren worden gedaan: afhankelijk van de rechthoekige coördinaten of de basisvectoren.

De vectoren die worden toegevoegd of afgetrokken naar de oorsprong van coördinaten kunnen worden gedaan, en vervolgens worden alle projecties opgesplitst in hun rechthoekige componenten in elk van de assen voor het vlak (x, y) of ruimte (x, x, en z); Ten slotte worden de componenten algebraïsch toegevoegd. Dus voor het vliegtuig is het:

Kan u van dienst zijn: Primo -nummers: kenmerken, voorbeelden, oefeningen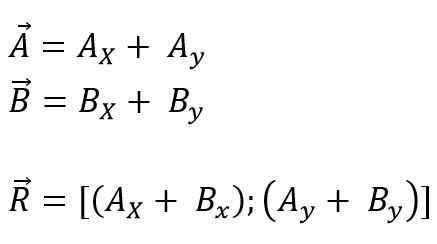

De resulterende vectormodule is:

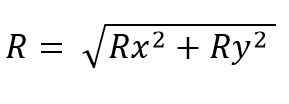
Terwijl het voor de ruimte is:

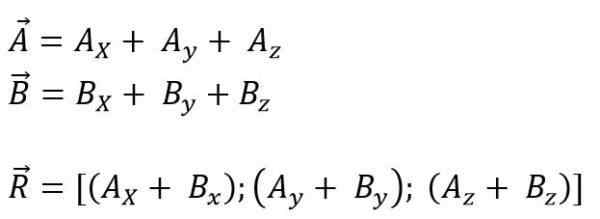
De resulterende vectormodule is:

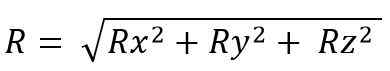
Wanneer vector -bedragen worden uitgevoerd, worden verschillende eigenschappen toegepast, die zijn:

• Associatief eigendom: Het resultaat verandert niet door eerst twee vectoren toe te voegen en vervolgens een derde vector toe te voegen.
• Gemeenschappelijk eigendom: De volgorde van de vectoren verandert het resultaat niet.
• Vector Distributive Eigendom: Als een scalaire wordt vermenigvuldigd met de som van twee vectoren, is deze gelijk aan de vermenigvuldiging van de scalaire voor elke vector.
• Distributieve eigenschap scalair: Als een vector wordt vermenigvuldigd met de som van twee scalars, is deze gelijk aan de vermenigvuldiging van de vector voor elke scalair.

Vector vermenigvuldiging

De vermenigvuldiging of het product van vectoren kan worden uitgevoerd als de som of aftrekking, maar daarbij verliest het de fysieke betekenis en valt het bijna nooit in de toepassingen. Daarom zijn over het algemeen de meest gebruikte soorten producten het scalaire en vectorproduct.

Scalair product

Het staat ook bekend als een punt van twee vectoren. Wanneer de twee -vectormodules worden vermenigvuldigd met de kleine hoek cosinus die ertussen wordt gevormd, wordt een scalair verkregen. Om een ​​scalair product tussen twee vectoren uit te drukken, wordt een punt daartussen geplaatst, en dit kan worden gedefinieerd als:

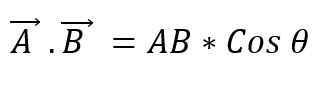
De waarde van de hoek die tussen de twee vectoren bestaat, hangt af van of deze parallel of loodrecht zijn; Je moet dus:

• Als de vectoren parallel zijn en hetzelfde gevoel hebben, coseno 0º = 1.
• Als de vectoren parallel zijn en tegengestelde zintuigen hebben, coseno 180º = -1.
• Als de vectoren loodrecht zijn, coseno 90º = 0.

Die hoek kan ook worden berekend, wetende dat:

Het scalaire product heeft de volgende eigenschappen:

• Commutatief eigendom: de volgorde van de vectoren verandert de scalair niet.
• Distributieve eigenschap: als een scalaire wordt vermenigvuldigd met de som van twee vectoren, is deze gelijk aan de vermenigvuldiging van scalair voor elke vector.

Vectorproduct

De vectorvermenigvuldiging, of kruisproduct van twee vectoren A en B, zal resulteren in een nieuwe vector C en drukt uit met een kruis tussen de vectoren:

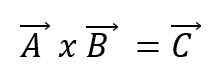
De nieuwe vector zal zijn eigen kenmerken hebben. Op die manier:

• De adres: Deze nieuwe vector zal loodrecht staan ​​op het vlak, dat wordt bepaald door de oorspronkelijke vectoren.
• Hij gevoel: Dit wordt bepaald met de rechterhandregel, waarbij de vector A naar de b wordt gericht die de richting van de rotatie met de vingers wijst, en met de duim de richting van de vector is gemarkeerd.
• Hij module: Het wordt bepaald door de vermenigvuldiging van de modules van de AXB -vectoren, door de boezem van de kleine hoek die tussen deze vectoren bestaat. Het wordt uitgedrukt:

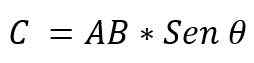
De waarde van de hoek die tussen de twee vectoren bestaat, hangt af van of deze parallel of loodrecht zijn. Het is dus mogelijk om het volgende te bevestigen:

• Als de vectoren parallel zijn en dezelfde betekenis hebben, sine 0º = 0.
• Als de vectoren parallel zijn en tegengestelde zintuigen hebben, sinus 180º = 0.
• Als de vectoren loodrecht zijn, sinus 90º = 1.

Wanneer een vectorproduct wordt uitgedrukt volgens zijn basisvectoren, moet het:

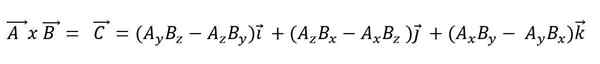
Het scalaire product heeft de volgende eigenschappen:

• Het is niet commutatief: de volgorde van de vectoren verandert de scalair.
• Distributieve eigenschap: als een scalaire wordt vermenigvuldigd met de som van twee vectoren, is deze gelijk aan de vermenigvuldiging van scalair voor elke vector.