De Morgan Laws

We leggen uit wat de wetten van Morgan zijn, we demonstreren ze en geven voorbeelden

Figuur 1.- De wiskundige Augustus van Morgan (1806-1871) en zijn wetten van propositionele logica. Bron: f. Zapata.

Wat zijn de wetten van de Morgan?

De wetten van de Morgan zijn twee logische wetten die behoren tot de propositionele logica die zijn geformuleerd door de Engelse wiskundige Augustus van Morgan (1806-1871). Ze stellen het volgende vast, met betrekking tot een samengestelde logische propositie:

1. Het tegenovergestelde van een conjunctie is gelijk aan de disjunctie die wordt gevormd met de tegenstellingen of ontkenningen van de voorstellen die de conjunctie vormen.
2. De ontkenning van disjunctie kan worden uitgedrukt als een conjunctie bestaande uit de tegenstellingen of ontkenningen van de stellingen die bij de disjunctie betrokken zijn.

In de notatie van propositionele logica worden de wetten van De Morgan op een compacte en formele manier uitgedrukt als deze:

1. ∼ (p ∧ q) ⇔ ∼P ∨Q
2. ∼ (p ∨ q) ⇔ ∼P ∧Q

Wat deze wetten uitdrukken, is dat het resultaat, hetzij in de weigering van conjunctie of disjunctie, gelijk is aan het afzonderlijk weigeren van elk van de deelnemende stellingen en de connector te investeren die hen verbindt.

Voor een beter begrip van de wetten van De Morgan, is het noodzakelijk om de betekenis van de stellingen en symbolen die worden gebruikt in de propositionele logica te beoordelen, om te zien hoe deze wetten gemakkelijk van toepassing zijn.

Logische notatie

Het basistool van propositionele logica is de stellingen. Een logische propositie is een verklaring die een werkelijke waarde, Of het waar of onwaar is, maar niet beide tegelijkertijd. Hierin is er geen dubbelzinnigheid toegestaan, dat wil zeggen, er kan geen twijfel bestaan.

Een propositie wordt aangeduid met een kleine letters, zoals in de volgende voorbeelden:

• Vraag: Mexico City is de hoofdstad van Mexico (waar).
• V: Door het toevoegen van 2 en 3, 4 (onwaar) wordt verkregen.
• A: Alle zoogdieren zijn landdieren (onwaar).

Kan je van dienst zijn: heptagon

Er zijn ook complexere stellingen, die zijn gestructureerd door het gebruik van eenvoudige stellingen, zoals deze:

• V: Carlos gaat naar de bioscoop als het niet regent.
• Vraag: ANA is een chemicus of mariene bioloog.
• A: Juan gaat uit eten of Pedro ziet het spel op televisie.

Logische connectoren

Logische connectoren zijn symbolen die worden gebruikt om eenvoudige proposities te koppelen en zo complexere proposities op te bouwen. In propositionele logica heeft elk van hen een bepaalde betekenis.

De meest gebruikte connectoren zijn conjunctie, disjunctie, exclusieve disjunctie, ontkenning, conditionaliteit en bi-conditionaliteit.

Voegwoord

De conjunctie wordt aangeduid met een omgekeerde "V" -brief. Een samengestelde propositie door een conjunctie wordt als volgt gesymboliseerd p ∧ q, als volgt:

• P ∧ Q: Mexico City is de hoofdstad van Mexico en is in Noord -Amerika.

Het is gemakkelijk om hier te identificeren dat P "Mexico City is de hoofdstad van Mexico" en Q is "is in Noord -Amerika".

Disjunctie

Twee soorten disjunctie worden onderscheiden: de zwakke en de exclusieve. A Zwakke disjunctie Het wordt gesymboliseerd door ∨ en in logische notatie zou het p ∨ q zijn. Voorbeeld van dit soort disjunctie is:

• P ∨ Q: Juan is een voetballer of Juan is een tennisspeler.

In plaats daarvan de Exclusieve disjunctie Het wordt gesymboliseerd door teken ⊻ en impliceert dat een van de stellingen moet worden uitgesloten, bijvoorbeeld:

P ⊻ Q: Alicia is 20 jaar oud of Alicia is 22 jaar oud.

Het verschil tussen beide typen is duidelijk, bij exclusieve disjunctie is een van de stellingen uitgesloten, want als Alicia 20 jaar oud is, kan hij niet 22 zijn en vice versa. Aan de andere kant, in de zwakke disjunctie, kan Juan tegelijkertijd een voetballer en tennisser zijn.

Ontkenning

Door het symbool ∼ een propositie te plaatsen, wordt dit geweigerd, zoals in:

• V: ∼ (Veracruz is de hoofdstad van Mexico).

Dat wordt gelezen als "Veracruz is niet de hoofdstad van Mexico". Andere manieren om een ​​ontkenning uit te drukken, afgezien van "nee", is door zinnen als "is vals", "het is een leugen dat" en "het niet waar is".

Kan u van dienst zijn: lineaire interpolatie

Voorwaarde

Het zijn samengestelde stellingen die meestal de woorden "ja" en "dan ..." gebruiken om twee stellingen te koppelen waarin er conditionaliteit is of implicatie. Het deel van de propositie dat wordt geschreven onmiddellijk nadat het "ja" is, is de antecedent golf hypothese van de propositie en wat na de term "dan" is, is de conclusie of als gevolg van gevolg.

Het symbool dat wordt gebruikt voor conditionaliteit is de pijl van links naar rechts "→", daarom wordt een conditionaliteit tussen twee stellingen weergegeven als P → Q, die kan worden gelezen als "als P, dan q". Bijvoorbeeld:

P → Q: Als het 's middags regent, speel ik geen tennis.

Bi-conditionaliteit

In dit type propositie wordt de uitdrukking "ja, en alleen als" om twee stellingen te verbinden, genaamd eerste en tweede biconditioneel lid worden gebruikt. Het gebruikte symbool is de bidirectionele pijl "↔".

De twee stellingen verbonden via "Ja, en alleen als" worden respectievelijk genoemd Eerst En Tweede lid en de bi-conditionaliteit van twee stellingen P en Q blijft als p ↔ q. Bijvoorbeeld:

P ↔ Q: Maria rijdt graag op een fiets als en alleen als de dag zonnig is.

Demonstratie van de wetten van De Morgan

De wetten van de Morgan maken deel uit van logische gelijkwaardigheid en kunnen worden aangetoond door de waarheidstabellen, die worden gebruikt om de waarheid (ware of onwaar) waarde van een propositie te kennen.

Omdat de conjunctie alleen waar is wanneer p en q waar zijn, is de waarheidstabel ervan:

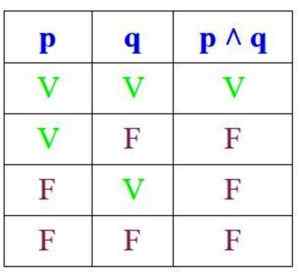
Aan de andere kant, in disjunctie, is de propositie waar als P en Q waar zijn of als er ten minste een van hen is, maar het is onwaar als beide zijn:

Kan u van dienst zijn: permutaties zonder herhaling: formules, demonstratie, oefeningen, voorbeelden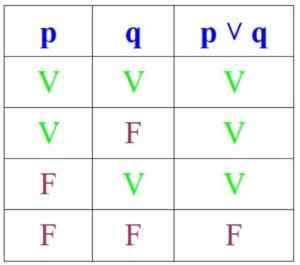

Nu verandert ontkenning de waarheid in vals en vice versa. In dit geval zijn de waarheidswaarden van ∼ (p ∧ q) en ∼ (p ∨ q) het tegenovergestelde van de waarheidswaarden (p ∧ q) en (p ∨ q):

En het moet worden geverifieerd dat deze resultaten worden verkregen bij het uitvoeren van de respectieve waarheidstabellen van (∼ P ˅ ∼ Q) en (∼ P ˄ ∼ Q):

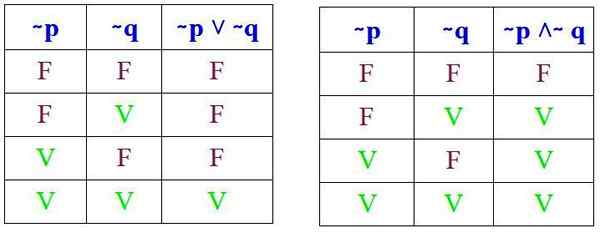
En inderdaad, bij het vergelijken van de respectieve waarheidstabellen, wordt opgemerkt dat de wetten van De Morgan zijn vervuld. Nu zullen er twee voorbeelden van de toepassing ervan worden gezien.

Opgelost voorbeeld 1

Pas de wetten van De Morgan toe om de equivalente expressie van: ∼ te vinden (∼P ˅ ∼Q)

• Oplossing

De gegeven expressie wordt ∼ vergeleken (∼P ˅ ∼Q) met de wet van Morgan:

∼ (p ∨ q) ⇔ ∼P ∧Q

En er wordt opgemerkt dat de ontkenning in beide gevallen al buiten de haakjes ligt, daarom worden de instructies van de wet gevolgd: het weigert ∼P, ontkent ∼Q en de connector wordt gewijzigd:

∼ (∼P ˅ ∼Q) ⇔ ∼ (∼P) ∧ ∼ (∼Q) ⇔ P ∧ q

Opgelost voorbeeld 2

Bepaal de equivalente expressie van ∼ [∼P ˄ ∼ (∼Q)] ≡

• Oplossing

Ten eerste is de ∼Q -ontkenning vereenvoudigd:

∼ [∼P ˄ ∼ (∼Q)] ⇔ ∼ [∼P ˄ q]

Omdat er al een ontkenning buiten de beugel is, wordt de resulterende uitdrukking vergeleken met de wet van Morgan: ∼ (p ∧ q) ⇔ ∼P ∨q

Om ∼ [∼P ˄ q] op te lossen, moet u ∼P ontkennen, q ontkennen en de connector wijzigen:

∼ [∼P ˄ q] ⇔∼ (∼P) ∨ ∼Q ⇔ P ˅ ∼Q

Referenties

1. Becerra, J.M.  Unam Logic Notes.
2. Briljant. Van de wetten van Morgan. Hersteld van: briljant.borg.
3. Elektronica -tutorials. Door Morgan's stelling. Hersteld van: elektronica-tormales.WS.
4. López, f. Inleiding tot wiskundige logica. Hersteld van: YouTube.com
5. Muñoz, c. Inleiding tot logica. Opgehaald van: websites.UCM.is.