OHM -wet en formule, berekening, voorbeelden, oefeningen

De De wet van Ohm, In zijn macroscopische vorm geeft het aan dat de spanning en intensiteit van de stroom in een circuit recht evenredig zijn, de weerstand is de evenredigheidsconstante. Door deze drie magnitudes aan te geven, zoals respectievelijk V, I en R, stelt de wet van Ohm vast dat: V = i.R.

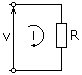
Evenzo is de wet van Ohm gegeneraliseerd om circuitelementen op te nemen die niet puur resistief zijn in wisselstroomcircuits, dus als volgt aangenomen: V = i. Z.

Figuur 1. De wet van Ohm is van toepassing op veel circuits. Bron: Wikimedia Commons. Tlapicka [CC BY-SA 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)]

Waar Z Het is de impedantie, die ook de oppositie vertegenwoordigt tegen de doorgang van de wisselstroom door een circuitelement, bijvoorbeeld een condensor of een inductie.

Opgemerkt moet worden dat niet alle circuitmaterialen en elementen voldoen aan de wet van Ohm. Aan die waarin het geldig is, worden elementen genoemd ohmisch, En waarin het niet wordt vervuld, worden ze genoemd No-ohmic of niet -lineair.

Veel voorkomende elektrische weerstanden zijn ohmisch, maar diodes en transistoren zijn dat niet, omdat de relatie tussen spanning en stroom niet lineair is.

De wet van Ohm is zijn naam verschuldigd aan de Duitse natuurkundige en wiskundige. Volgens hem is de eenheid voor elektrische weerstand in het internationale systeem benoemd: de OHM, die ook wordt uitgedrukt door de Griekse brief ω.

[TOC]

Hoe wordt het berekend?

Hoewel de macroscopische vorm van de wet van Ohm de bekendste is, omdat het bedragen verbindt die gemakkelijk meetbaar zijn in het laboratorium, de Microscopische vorm Relateert twee belangrijke vectorhoeveelheden: het elektrische veld EN en huidige dichtheid J:

J = σ.EN

Waarbij σ de elektrische geleidbaarheid van het materiaal is, een eigenschap die aangeeft hoe het gemak moet worden gestimuleerd om de stroom te stimuleren. Voor zijn deel J Het is een vector waarvan de grootte het quotiënt is tussen de huidige intensiteit I en het gebied van de dwarsdoorsnede waarnaar het circuleert.

Het kan u van dienst zijn: oppervlakkige golven: kenmerken, typen en voorbeelden

Het is logisch om aan te nemen dat er een natuurlijke verbinding is tussen het elektrische veld in een materiaal en de elektrische stroom die er doorheen circuleert, zoals de grootste vaker voorkomt.

Maar de stroom is geen vector, omdat het geen adres in de ruimte heeft. In plaats daarvan de vector J Het is loodrecht - of normaal - naar het kruis -sectionele gebied van de bestuurder en de betekenis ervan is dat van de stroom.

Uit deze vorm van de wet van Ohm wordt de eerste vergelijking bereikt, uitgaande van een stuurprogramma en dwarsdoorsnede A, en het vervangen van de magnitudes van J En EN door:

J = I/A

E = v/ℓ

J = σ.E → I/A = σ. ((V/ℓ)

V = (ℓ/σ.NAAR).Je

Het omgekeerde van geleidbaarheid wordt genoemd weerstand En het wordt aangeduid met de Griekse letter ρ:

1/ σ = ρ

Daarom:

V = (ρℓ/ a).I = r.Je

De weerstand van een bestuurder

In de vergelijking V = (ρℓ/ a).Je, De constante ((ρℓ/ a) Het is daarom weerstand:

R = ρℓ/ a

Weerstand van de bestuurder hangt af van drie factoren:

-Zijn weerstand ρ, typisch voor het materiaal waarmee hij wordt vervaardigd.

-De lengte ℓ.

-Gebied A van de dwarsdoorsnede.

Een grotere ℓ, grotere weerstand, omdat huidige dragers meer mogelijkheden hebben om te botsen met de andere deeltjes in de bestuurder en energie te verliezen. En integendeel, naar grotere A, is het gemakkelijker voor huidige dragers om op een ordelijke manier door het materiaal te bewegen.

Ten slotte ligt in de moleculaire structuur van elk materiaal het gemak waarmee een stof de elektrische stroom laat passeren. Dus bijvoorbeeld metalen zoals koper, goud, zilver en platina, met lage weerstand, zijn goede geleiders, terwijl hout, rubber en olie dat niet zijn, dus ze hebben grotere weerstand.

Voorbeelden

Hier zijn twee illustratieve voorbeelden van de wet van Ohm.

Experimenteer om de wet van Ohm te controleren

Een eenvoudige ervaring illustreert de wet van Ohm, voor dit een stuk geleidend materiaal, een variabele spanningsbron en een multimeter is nodig.

Kan u van dienst zijn: drukmeters

Onder de uiteinden van het geleidende materiaal wordt een spanning V vastgesteld die geleidelijk moet variëren. Met de variabele stroombron kunnen de waarden van genoemde spanning worden vastgesteld, die worden gemeten met de multimeter, evenals de stroom die ik door de bestuurder circuleert.

De paren van waarden V en ik zijn opgenomen in een tabel en daarmee is een grafiek op millimeter papier gebouwd. Als de resulterende curve een lijn is, is het materiaal ohmisch, maar als het een andere curve is, is het materiaal niet -OHMIC.

In het eerste geval kan de helling van de lijn worden bepaald, die gelijkwaardig is aan de weerstand van de bestuurder of aan zijn omgekeerde, de geleiding.

In de volgende afbeelding vertegenwoordigt de blauwe lijn een van deze afbeeldingen voor een ohmmateriaal. Ondertussen zijn gele en rode krommen van niet-ohmische materialen, zoals een halfgeleider, bijvoorbeeld.

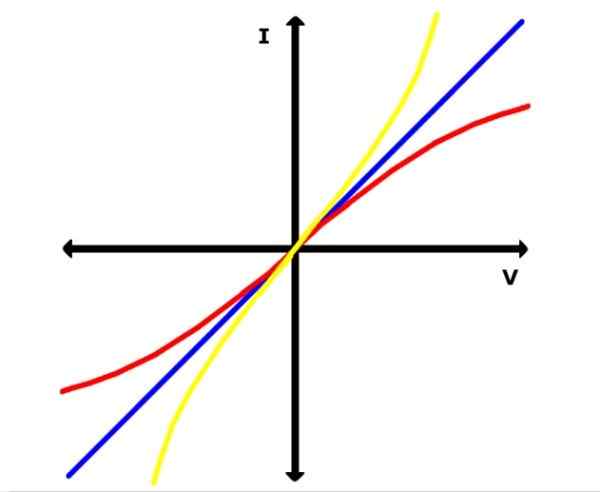Figuur 2. Grafiek I vs. V voor ohmische materialen (blauw recht) en niet-OSOHMIC-materialen. Bron: Wikimedia Commons.

Hydraulische analogie van de wet van Ohm

Het is interessant om te weten dat de elektrische stroom in de OHM -wet op een bepaalde manier een soortgelijk gedrag heeft dat van water dat door een pijp circuleert. De Engelse fysicus Oliver Lodge was de eerste die de simulatie van huidig ​​gedrag voorstelde door hydraulische elementen.

De leidingen vertegenwoordigen bijvoorbeeld de geleiders, omdat het water door hen en de huidige dragers door het laatste circuleert. Wanneer er een vernauwing in de pijp is, is de waterpassage moeilijk, dus dit zou gelijkwaardig zijn aan elektrische weerstand.

Het drukverschil aan twee uiteinden van de buis zorgt ervoor dat water stroomt, wat een hoogteverschil of een waterpomp oplevert, en analoog, het potentiële verschil (de batterij) is degene die de bewegende belasting houdt, equivalent aan stroming of volume van water per tijdseenheid.

Het kan u van dienst zijn: convectiewarmteoverdracht (met voorbeelden)

Een zuigerpomp zou de rol van een alternatieve spanningsbron vertegenwoordigen, maar het voordeel van het plaatsen van een waterpomp is dat het hydraulische circuit gesloten zou zijn, omdat een elektrisch circuit zou moeten zijn om stroomstroom te zijn.

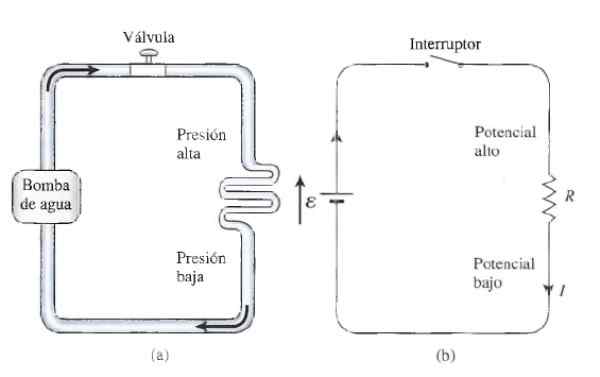figuur 3. Hydraulische analogie voor ohmwet: in a) een waterstroomsysteem en in b) een eenvoudig resistief circuit. Bron: Tippens, P. 2011. Fysica: concepten en toepassingen. 7e editie. McGraw Hill.

Weerstanden en schakelaars

Het equivalent van een schakelaar in een circuit zou een doorgangssleutel zijn. Het wordt op deze manier geïnterpreteerd: als het circuit open is (gesloten doorgang), kan de stroom en het water niet stromen.

Aan de andere kant, met de gesloten schakelaar (volledig open stappentoets) zowel de stroom als het water kan circuleren zonder problemen door de bestuurder of pijp.

De doorgangssleutel of klep kan ook een weerstand vertegenwoordigen: wanneer de sleutel volledig wordt geopend, is deze gelijk aan het hebben van een nulweerstand of kortsluiting. Als het überhaupt sluit, is het alsof je het open circuit hebt, terwijl het gedeeltelijk gesloten is, is het als een weerstand van een bepaalde waarde (zie figuur 3).

Opdrachten

- Oefening 1

Het is bekend dat een elektrische plaat 2 A op 120 V vereist om goed te werken. Wat is uw weerstand?

Oplossing

Het verzet wordt vrijgemaakt van de wet van Ohm:

R = v/ i = 120 V/ 2 a = 60 Ω

- Oefening 2

Een diameter van een diameter van 3 mm en 150 m lang heeft 3 3.00 Ω bij 20 ° C. Vind de weerstand van het materiaal.

Oplossing

De vergelijking R = ρℓ/ a is geschikt, Daarom is het noodzakelijk om eerst het gebied van de dwarsdoorsnede te vinden:

A = π(D/2)² = π (3 x 10^-3 m/2)² = 4.5π x 10 ^-6 M²

Eindelijk krijgt u bij het vervangen van:

ρ = a.R /ℓ = 4.5π x 10 ^-6 M² x 3 Ω / 150 m = 2.83 x 10 ^-7 Ω.M

Referenties

1. Resnick, r. 1992.Fysiek. Derde editie uitgebreid in het Spaans. Deel 2. Continental Editorial Company s.NAAR. van C.V.
2. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14^e. ED. Deel 2. 817-820.
3. Serway, r., Jewett, J. 2009. Natuurkunde voor wetenschap en engineering met moderne fysica. 7e editie. Deel 2. Cengage leren. 752-775.
4. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. McGraw Hill.
5. Sevilla University. Afdeling Applied Physics III. Dichtheid en huidige intensiteit. Hersteld van: ons.is.
6. Walker, J. 2008. Natuurkunde. 4e ed. Pearson.725-728