Tekent wet

We leggen de wet van tekenen uit, met voorbeelden en oefeningen opgelost

Schema van de tekenenwetgeving

Wat is de wet van tekenen?

De Tekent wet Het is de set regels die worden gebruikt in rekenkundige en algebraïsche berekeningen met reële getallen om het teken correct aan het resultaat toe te wijzen, wanneer zowel positieve als negatieve hoeveelheden betrokken zijn.

Er zijn voldoende regels volgens de uitgevoerd operatie: som, aftrekking, vermenigvuldiging en divisie, die de meest basale zijn, en er zijn ook regels voor tekenen met betrekking tot potentiëring en archiveringsoperaties.

In een bepaalde bewerking, hetzij met de hand of met rekenmachine, is het noodzakelijk om de wet van de tekenen correct toe te passen om een ​​correct resultaat te garanderen, omdat slechts een kleine wijziging in de tekens de bedragen aanzienlijk verandert.

De wet van de tekenen voor elke fundamentele rekenkundige bewerking en de gevallen die zich kunnen voordoen, worden hieronder onderzocht.

Wet van tekenen in som

1) Als de te toegevoegde nummers hetzelfde teken hebben

De cijfers worden zoals gewoonlijk toegevoegd en het resultaat wordt toegevoegd aan het teken van de getallen, ongeacht of dit positief of negatief is.

Het is belangrijk om in gedachten te houden dat positieve cijfers meestal niet vóór het teken zijn, maar rechtstreeks zijn geschreven. Aan de andere kant worden negatieve getallen tussen haakjes geschreven, vooral wanneer ze worden voorafgegaan door het symbool van een rekenkundige bewerking, om verwarring te voorkomen.

Voorbeelden van sommen getallen met hetzelfde teken:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Als de te toegevoegde nummers een ander teken hebben

De cijfers worden afgetrokken en het teken van het nummer dat de grootste absolute waarde heeft, wordt toegevoegd aan het resultaat, of het nu positief of negatief is.

Als voorbeeld wordt bewerking 5 + (−14) uitgevoerd. Omdat de absolute waarde van (−14) groter is dan de absolute waarde van 5, worden 5 eenheden afgetrokken van 14, wat 9 geeft en dit resultaat wordt een negatief teken geplaatst:

Kan u van dienst zijn: prisma's en piramides

5 + (−14) = −9

Meer voorbeelden van deze regel toegepast op de som van twee nummers van verschillende tekens zijn:

(−27) + 12 = −15

12 + (−7) = 5

Als er in de bewerking meer dan twee toevoegingen met verschillende tekens zijn, de Associatieve eigenschap van de som:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

De bewerking wordt eerst uitgevoerd in Pracete, die bestaat uit de som van twee nummers van verschillende tekens, waarvoor de beschreven regel wordt toegepast: het resultaat wordt afgetrokken en het teken van het nummer met de hoogste absolute waarde:

(−20) + 9 = −11

De bewerking is als volgt:

(−20) + 9 + (−7) = (−11) + (−7)

Nu heb je de som van twee getallen van hetzelfde teken, dan worden ze normaal toegevoegd en het resultaat wordt een negatief teken geplaatst:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Tekens in de vervanger

De aftrekking van twee getallen wordt gedefinieerd als de som van het tegenovergestelde. Op zijn beurt wordt het tegenovergestelde van een nummer gezegd nummer met het gewijzigde teken. Het tegenovergestelde van 2 is bijvoorbeeld (−2), het tegenovergestelde van (−5) is 5 enzovoort.

Met dit in gedachten, wanneer u de aftrekking van twee getallen hebt:

A - B

Het verandert eenvoudig in de som van het tegenovergestelde van B:

A + ( - B)

En ga verder zoals beschreven in de vorige sectie. Opmerking om een ​​teken te plaatsen + een negatief getal verandert het niet, maar zeer voorzichtig, het tegenovergestelde is niet waar.

Wanneer het getal "a", dat de minuend is, groter is dan het aantal "b", dat wordt gestolen, werkt als in de aftrekking van natuurlijke getallen. Geen probleem, omdat een groot aantal van een kleinere hoeveelheid wordt afgetrokken:

Kan u van dienst zijn: ongelijkheid van de driehoek: demonstratie, voorbeelden, opgeloste oefeningen

25 - 8 = 17

Met de volgende voorbeelden is de methode om het tegenovergestelde toe te voegen om af te trekken erg handig:

(−5) - 24 = (−5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55

Wet van tekenen in vermenigvuldiging

De wet van de tekenen in vermenigvuldiging wordt op deze manier toegepast:

• Door twee getallen van hetzelfde teken te vermenigvuldigen, is het resultaat altijd positief.
• Het product van twee tegengestelde tekennummers is altijd negatief.

De samenvatting van de tekensregel voor vermenigvuldiging wordt weergegeven in de afbeelding:

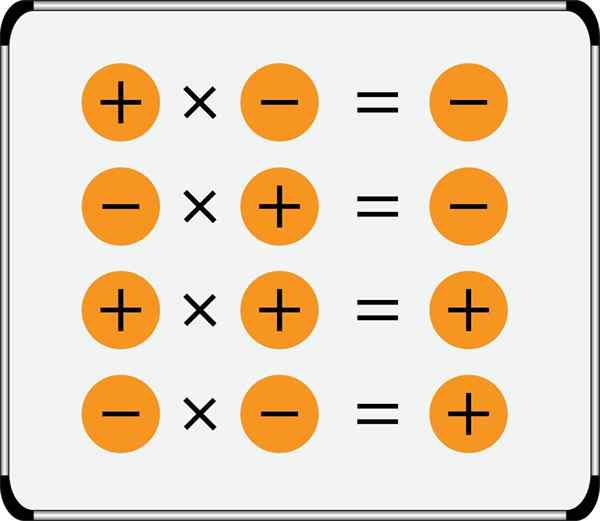
Merk op dat positieve getallen kunnen worden geschreven zonder het voorgaande teken, maar negatieve getallen hebben het altijd, bovendien worden twee rekenmeters symbolen nooit aan elkaar geschreven, ze moeten altijd worden gescheiden door een haakjes, bijvoorbeeld:

Niet correct: 3 × −4
Juist: 3 × (−4) = −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

Om meer dan twee getallen te vermenigvuldigen, wordt de associatieve eigenschap van vermenigvuldiging gebruikt, omdat de volgorde van de factoren het product bijvoorbeeld niet wijzigen bij het uitvoeren van:

(−2) × (−14) × 16

U kunt de eerste twee factoren, of de laatste twee als u wilt, vermenigvuldigen en het resultaat vervolgens vermenigvuldigen met de resterende factor. In dit geval worden de twee factoren eerst aan de linkerkant vermenigvuldigd:

[(−2) × (−14)] × 16

Het product van twee negatieve getallen is positief, dan (−2) × (−14) = 28 en blijft:

28 × 16 = 448

Wet van tekenen in divisie

Het is analoog aan de regel van tekenen voor vermenigvuldiging:

• De verhouding van twee getallen van hetzelfde teken is altijd positief.
• Door twee anders tekennummers te delen, is het resultaat altijd negatief.

Het kan u van dienst zijn: verschil tussen cirkel en omtrek (met voorbeelden)

Bijvoorbeeld:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Wet van tekenen in empowerment en indiening

Een schriftelijke nummer exponent is:

naar^N

Waar "a" de basis is en "n" is de exponent. Volgens de pariteit van de exponent worden twee gevallen onderscheiden:

Geval 1: A is positief

Wanneer de basis positief is, is het resultaat positief, ongeacht of de exponent gelijk of vreemd is, zoals in:

2³ = 8
3⁴ = 81

Geval 2: A is negatief

Hier zijn twee gevallen:

• Wanneer de exponent gelijk is, dan is het resultaat positief.
• Als de exponent vreemd is, is deze negatief.

Voorbeelden

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Bewerkingen met groeperingssymbolen

Ze verschijnen vaak afzonderlijke bewerkingen met groeperingssymbolen: haakjes, beugels en sleutels. Deze worden van binnenuit geëlimineerd, rekening houdend met het volgende:

• Als een groeperingssymbool wordt voorafgegaan door een positief teken, kan het worden verwijderd zonder de tekenen van de inhoud te wijzigen, bijvoorbeeld: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
• Als een negatief teken voorafgaat aan het groepssymbool, wordt het ingetrokken door het teken van de inhoud te investeren, bijvoorbeeld: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• Wanneer er samengevatte bewerkingen zijn, kunnen aftrekking, vermenigvuldiging en divisie de associatieve en distributieve eigenschappen worden gebruikt voor gemak.

Opgeloste oefeningen

a) 10 + 10

Oplossing: 20

b) (-8) + (-3)

Oplossing: -11

c) (3) + (-10) 

Oplossing: -7

d) (5) x (-3)

Oplossing: -15

e) (-10) x (-10)

Oplossing: 100

f) (18) ÷ (-3)

Oplossing: -6

G) (-10) ÷ (-2)

Oplossing: 5

h) 4 - ( - 7 + 9)

Oplossing: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11− 9 = 2