Fick's wet

Wat is de wet van Fick?

De Fick's wet Het is een wiskundige vergelijking die de massastroom relateert in een medium met de concentraties of drukgradiënt. Het werd geformuleerd in 1855 door de Duitse fysioloog en arts Adolf Fick, die geïnspireerd was door Fourier's wetten (thermische geleiding) en OHM (elektrische geleiding), modelleerde het diffusieproces van zuurstof naar de alveoli van de longen van de longen.

De wet van Fick presenteert de bijzonderheid dat het niet alleen van toepassing is op chemische of biochemische diffusiefenomenen, maar ook voor die van welke aard dan ook. Daarom dient het om de verspreiding van atomen tussen vaste stoffen te modelleren, die zeer nuttig zijn in de fysica van materialen en engineering.

Weergave van een diffusieproces door een semipermeabiel membraan. Bron: Gabriel Bolívar.

De centrale basis is echter hetzelfde voor bijna alle diffusiefenomenen, die hierboven wordt geïllustreerd. Paarse deeltjes, zijn atomen of moleculen, worden verspreid door een semipermeable dikke membraan L en transversaal gebied naar. Links hebben we een grotere concentratie C₁ van deeltjes die rechts, c₂.

De wet van Fick stelt het volgende vast: de massastroom die door een oppervlak wordt verspreid, is evenredig met de concentratiegradiënt (C₂-C₁/L) en een constante d diffusie of diffusiviteitscoëfficiënt genoemd.

Deze wet heeft twee vormen: één gebaseerd op ruimte (x) en een andere afhankelijk van ruimte en tijd (x, t). De eerste is van toepassing op systemen in stationaire omstandigheden, terwijl de tweede voor echte, niet -stationaire systemen.

Fick's eerste wet

Componenten en vergelijking

De dikke L van het semipermeabele membraan vertegenwoordigt de afstand (x) dat de deeltjes moeten reizen om de andere kant te bereiken. Zoals te zien in het beeld, gaan paarse deeltjes hoe meer ze weggaan van het linker compartiment, waar c₁ Het is geweldig, de concentratie neemt af tot de waarde van C₂. Dat wil zeggen, de concentratie verandert langs de dikte van het membraan, afhankelijk van X.

Deze concentratievariatie afhankelijk van afstand is wat bekend staat als concentratiegradiënt: (C₂-C₁)/L o (c₂-C₁)/X. Merk op dat de waarde ervan negatief is (-1), omdat C₂ > C₁.

Aan de andere kant hebben we ook de snelheid waarmee de deeltjes door het membraan of de ruimte in kwestie worden verspreid. Deze snelheid hangt af van de grootte en massa van de deeltjes, evenals de aard van de omgeving en temperatuur. De diffusiecoëfficiënt d vertegenwoordigt deze snelheid en kan constant zijn of niet tijdens diffusie.

Kan u van dienst zijn: laboratoriumfilter): kenmerken, functies, typen

En ten slotte hebben we een massastroom 'J' die het dwarse gebied van het membraan of het kanaal kruist waar de deeltjes zich verspreiden. Als je deze voorwaarden groepeert, is de vergelijking van Fick's eerste wet geboren:

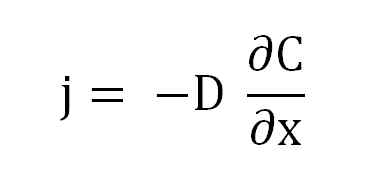Vergelijking van Fick's eerste wet. Bron: Gabriel Bolívar.

Waarbij J evenredig is met D en A (∂c/∂x), de concentratiegradiënt.

Interpretatie en eenheden

Het negatieve symbool in de vergelijking dient om het negatieve teken van de concentraties gradiënt te neutraliseren. Anders zou J een negatieve waarde hebben, die onduidelijk is. Evenzo is de waarde van D positief, zodat het door het negatieve teken dat voorafgaat, een negatieve waarde geeft.

De eerste wet van Fick geeft het volgende aan: hoe groter de concentratiegradiënt (∂c/∂x), hoe groter de massastroom j. Dat wil zeggen het verschil tussen C₂ en C₁ Het wordt groter en daarom zullen meer deeltjes zich door het membraan verspreiden.

Aan de andere kant hangt J ook af van D, die op zijn beurt afhankelijk is van parameters zoals temperatuur, viscositeit, molecuulgewicht en het transversale gebied om:

D ∝ (A/L) (S/√m_W))

Waar s de oplosbaarheid is van het deeltje dat wordt verspreid met de omgeving, en m_W Zijn molecuulgewicht.

Wat betreft de eenheden van de componenten of voorwaarden van de vergelijking die we hebben:

-C (kg · m^-3 of mol · m^-3))

-D (m^-2· S^-1))

-J (kg · m^-2· S^-1 of mol · m^-2· S^-1))

Netto medium kwadratische verplaatsing

Tijdens de verspreiding botsen de deeltjes met elkaar en eindigen na korte tijdsintervallen enorme afstanden Δx. Afhankelijk van de betekenis van deze verplaatsingen kan Ax echter negatieve of positieve waarden hebben (volgens een punt van oorsprong). Dat is de reden waarom het gemiddelde van de Δx -waarden voor alle moleculen neigt naar 0.

Aan de andere kant zijn de AX -waarden erg klein in vergelijking met de afstanden die de deeltjes lopen. Wanneer ze botsen, verliezen ze mobiliteit in de richting van een richting, bijgevolg een beperkte netto verplaatsing; Bijvoorbeeld 2 cm vooruitgang in één richting na het reizen honderden meters in botsingen en rebounds.

Einstein vond in 1905 een wiskundige uitdrukking voor de gemiddelde rol van de verplaatsing (daarom verschillend van 0):

<(Δx)²> = 2dt

Het definiëren

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_Rms Het is de gemiddelde netto kwadratische verplaatsing van de deeltjes in kwestie. (Δx)_Rms Het vertelt ons hoeveel deeltjes gemiddeld beweegt (in een positieve of negatieve richting) volgens de tijd. Sommige deeltjes zullen verdere of dichtstbijzijnde afstanden verplaatsen dan (Δx)_Rms, Een Gaussiaanse verdeling veroorzaken.

Kan u van dienst zijn: calciumoxide (CAO)

Fick Second Law

Vergelijking

De eerste wet van Fick beschrijft de diffusie in stationaire omstandigheden, dat wil zeggen dat de massastroom J niet in de loop van de tijd varieert. In echte systemen hebben we echter niet -stationaire omstandigheden, waarbij massastroom niet alleen in de ruimte varieert, maar ook in de tijd. Daarom is het geïnteresseerd in het bepalen (∂c/∂t).

Hieronder hebben we twee vergelijkingen die de tweede wet van Fick vertegenwoordigen:

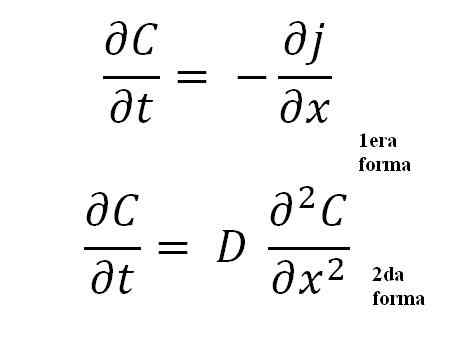Vergelijkingen van Fick's tweede wet. Bron: Gabriel Bolívar.

De 2e vorm is de belangrijkste van allemaal, omdat het de algemene wiskundige vergelijking voor elk verspreidingsproces vertegenwoordigt; ofwel thermisch, elektrisch, atomair, enz.

Aftrek

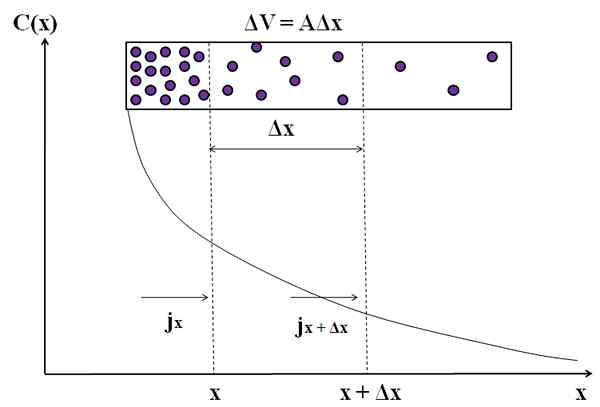Grafische weergave van hoe massastroom niet constant is in de verspreiding van deze moleculen. Bron: Gabriel Bolívar.

Overweeg opnieuw paarse deeltjes in een rechthoekige kamer. Onder de afstanden x en x+Δx hebben we een stroom j_X (Inkomend) en J_x+Δx (extravert). Het volume van de camera tussen deze afstanden wordt bepaald door:

ΔV = aδx

Merk op dat grafiek C (x) vs x geen rechte lijn afkomstig is, dus we hebben verschillende waarden van J (j_X ≠ j_x+Δx)). We moeten Δc/Δt bepalen.

De massa m_X Het zal gelijk zijn aan:

M_X = J_X Aδt

Een dimensionale analyse helpt om te begrijpen waarom:

kg = (kg · m^-2· S^-1) (M²) (S)

Op dezelfde manier berekenen we m_x+Δx:

M_{x+ Δx} = J_x+Δx Aδt

Zijnde de massa die zich ophoopt in dat gebied gelijk aan AM:

Δm = m_X - M_{x+ Δx}

= (j_X - J_{x+ Δx}) Aδt

= -(j_{x+ Δx} - J_X) Aδt

= -AJaAt

En wetende dat Δc = Δm/ΔV

ΔC = -AJAAt/ ΔV

= -AJaAt /aδx

= -AJAt/Δx

We wissen Δc/Δt

ΔC/Δt = -AJ/Δx

Deze uitdrukking geeft aan dat de variatie van de concentratie in de tijd gelijk is aan de variatie van de J -stroom ten opzichte van zijn verplaatsing. Door de limieten toe te passen voor Δt en Δx die op 0 verzorgt, krijgen we dezelfde uitdrukking als een gedeeltelijke derivaat:

∂c/∂t = -(∂j/∂x) (1e vorm)

Ten slotte wordt de 2e vorm verkregen door J te vervangen door Fick's eerste wet:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (2e vorm)

Opgeloste oefeningen

In de volgende oefeningen zullen zeer eenvoudige systemen worden overwogen wiens onbekenden kunnen worden opgelost met behulp van Fick's eerste wet.

Oefening 1

Stelling

In een pijp 15 meter lang en 21 centimeter breed, en die ook verzadigd is met stikstof, wordt een zuurstofstroom verspreid van het ene uiteinde naar het andere bij een temperatuur van 0 ºC. Wetende dat de druk aan de linkerkant (P₁) is 20 kg/m³, En dat de druk aan de rechterkant (P₂) is 10 kg, bepaal:

Het kan u van dienst zijn: Hydronio ion

a) de verspreiding van de massastroom

b) Hoeveel kilogram van of₂ Ze zullen zich over 17 minuten door de pijp verspreiden?

c) de concentratiegradiënt of druk

d) de druk van O₂ op een afstand van 7 meter van de ingang van de pijpleiding

e) Hoeveel zal 80 kg o o₂ Bij het verspreiden van deze pijp?

Bedenk dat D_O2-N2 is gelijk aan 1.8 · 10^-5 M²· S^-1.

Oplossing

Uit Fick's eerste wet moeten we subsectie oplossen a):

J = -d (p₂-P₁)/L

= -(1.8 · 10^-5 M²· S^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

Om te b) We hebben het pijpgebied nodig:

A = π (0.21 m)²

= 0.14 m²

En we vermenigvuldigen J met een en tijd T om de massa van of te bepalen₂ Uitgeput:

M_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²))

= 3.57 · 10^-5 kg

Nu, voor subsectie c) hebben we dat de gradiënt gelijk is aan:

Gradiënt = (p₂-P₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Maar we nemen de positieve waarde, wat fysiek logisch is:

2/3 (kg/m³) · M^-1

Deze waarde zal ons dan dienen om de onderafdeling op te lossen d) Als de gradiënt goed wordt geïnterpreteerd: elke meter de druk van of₂ 2/3 kg/m zal vallen³. Door 7 meter te verspreiden, zullen we hebben:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 of 4.7 kg/m³

Dat wil zeggen, de druk op die afstand zal zijn:

(20-4.7) (kg/m³) = 15.3 kg/m³

En ten slotte, subsectie E) is vergelijkbaar met B), alleen dat we nu tijd wissen en niet de massa:

M_O2 = Jat

t = m_O2/JA

= (80 kg)/(1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²))

= 47619.04 s of 0.55 dagen

Oefening 2

Stelling

Bepalen (Δx)_Rms Voor sucrose in water bij t = 1 min, 1 uur en 1 dag. De verspreidingscoëfficiënt van sucrose in water is 0.52 · 10^-5cm²· S^-1.

Oplossing

We passen de vergelijking toe:

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

We evalueren (Δx)_Rms Met de tijd die in seconden wordt uitgedrukt. Voor t = 1 min of 60 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (60s))^1/2

= 0.025 cm

Voor t = 1 H of 3600 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (3600s))^1/2

= 0.19 cm

En ten slotte voor t = 1 dag of 86400 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (86400S))^1/2

= 0.95 cm

Merk op dat naarmate de tijd verstrijkt, de sucrose -moleculen niet eens in staat zijn geweest om 1 cm in enige richtingen te verplaatsen.

Referenties

1. Walter J. Moore. (1963). Fysische chemie. In chemische kinetiek. Vierde editie, Longmans.
2. Iran. Levine. (2009). Principes van fysicochemie. Zesde editie. MC Graw Hill.
3. Inleiding tot materiaalwetenschap en engineering. (11 maart 2018). Fick's tweede wet. Profit. Rajesh Prasad. [VIDEO]. Hersteld van: YouTube.com
4. Wikipedia. (2020). Fick's wetten van diffusie. Opgehaald uit: in.Wikipedia.borg
5. Laura Dickson. (10 september 2020). Diffusie. Chemistry Libhethexts. Hersteld van: chem.Librhetxts.borg
6. Larissa Zhou et al. (1 september 2015). Inzicht in de diffusietheorie en de wet van Fick door voedsel en koken. De American Physiological Society. doen.org/10.1152/Advan.00133.2014