Faraday Formula Law, eenheden, experimenten, oefening,

De Faraday Law In elektromagnetisme stelt het vast dat een veranderende magnetische veldstroom een ​​elektrische stroom in een gesloten circuit kan induceren.

In 1831 ervoer de Engelse natuurkundige Michael Faraday bewegende bestuurders in een magnetisch veld en ook variërende magnetische velden die vaste stuurprogramma's kruisten.

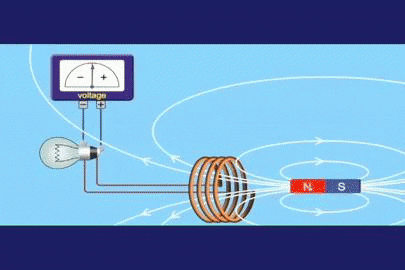Figuur 1. Faraday Induction Experiment

Faraday besefte dat als hij de magnetische veldstroom in de tijd varieerde, hij in staat was om een ​​spanning te vestigen die evenredig is met die variatie. Als ε de geïnduceerde elektromotorische spanning of kracht (geïnduceerde FEM) is en φ de magnetische veldstroom is, kan deze in wiskundige vorm worden uitgedrukt:

| ε | = Δφ/Δt

Waarbij het symbool δ de variatie van de hoeveelheid aangeeft en de balken in de FEM de absolute waarde hiervan aangeven. Omdat het een gesloten circuit is, kan de stroom in een of andere richting circuleren.

De magnetische flux, geproduceerd door een magnetisch veld door een oppervlak, kan bijvoorbeeld op verschillende manieren variëren:

-Een staafmagneet door een cirkelvormige spiraal verplaatsen.

-Het verhogen of verminderen van de intensiteit van het magnetische veld dat de lus kruist.

-Het veld laten vasthouden, maar door een bepaald mechanisme verandert het gebied van de lus.

-Het combineren van de bovenstaande methoden.

Figuur 2. De Engelse natuurkundige Michael Faraday (1791-1867).

[TOC]

Formules en eenheden

Stel dat er een gesloten circuit van gebied A is, zoals een cirkelvormige spiraal of een verzekering gelijk aan figuur 1, en dat er een magneet is die een magnetisch veld produceert B.

De magnetische veldstroom φ is een scalaire hoeveelheid die verwijst naar de hoeveelheid veldlijnen die het gebied overschrijden. In figuur 1 zijn de witte lijnen die de noordelijke paal van de magneet verlaten en terugkeren in het zuiden.

Kan u van dienst zijn: Brayton Cycle: Process, Efficiency, Toepassingen, Oefeningen

De intensiteit van het veld zal evenredig zijn met het aantal lijnen per eenheid van het gebied, dus we kunnen zien dat het bij de polen zeer intens is. Maar we kunnen een zeer intens veld hebben dat geen stroom in de lus veroorzaakt, die we kunnen bereiken door de oriëntatie hiervan (of de magneet) te veranderen.

Om rekening te houden met de oriëntatiefactor, wordt de magnetische veldstroom gedefinieerd als het scalaire product tussen B En N, wezen N De normale eenheidsvector naar het oppervlak van de spase en dat duidt op de oriëntatie ervan:

Φ = B•N A = BA.cosθ

Waar θ de hoek is tussen B En N. Als bijvoorbeeld B En N Ze staan ​​loodrecht, de magnetische veldstroom is nietig, omdat in dat geval het veld raakt aan het spase -vlak en het oppervlak niet kan oversteken.

In plaats van B En N Ze zijn parallel, het betekent dat het veld loodrecht staat op het spira -vlak en de lijnen er maximaal doorheen gaan.

De internationale systeemeenheid voor F is de Weber (W), waarbij 1 W = 1 T.M² (leest "Tesla per vierkante meter").

Lenz -wet 

In figuur 1 kunnen we zien dat de polariteit van de spanning verandert naarmate de magneet beweegt. Polariteit wordt vastgesteld door de wet van Lenz, die stelt dat de geïnduceerde spanning zich moet verzetten tegen de variatie die deze produceert.

Als bijvoorbeeld de door de magneet geproduceerde magnetische flux toeneemt, vestigt de bestuurder een stroom die circuleert met het creëren van zijn eigen stroom, die zich verzet tegen deze toename.

Als de door de magneet gecreëerde stroom daarentegen afneemt, circuleert de geïnduceerde stroom zodanig dat zijn eigen stroom de afname tegengaat.

Kan u van dienst zijn: thermometrische schalen

Om dit fenomeen rekening te houden, wordt eerder een negatief teken voor de wet van Faraday geplaatst en het is niet langer nodig om de absolute waardebars te plaatsen:

ε = -δφ/Δt

Dit is de wet van Faraday-Lenz. Als de stroomvariatie oneindig is, worden delta's vervangen door differentiëlen:

ε = -dφ/dt

De vorige vergelijking is geldig voor een lus. Maar als we een draaiende spoel hebben, is het resultaat veel beter, omdat de FEM zich n keer vermenigvuldigt:

ε = - n (dφ/dt)

Faraday -experimenten

Om de stroom te produceren die de gloeilamp verlicht, moet er tussen de magneet en de spiraal een relatieve beweging zijn. Dit is een van de manieren waarop de stroom kan variëren, omdat op deze manier de intensiteit van het veld dat de lus kruist, verandert.

Op dit moment stopt de magneetbeweging, de lamp gaat uit, zelfs als de magneet nog in de spase blijft. Wat nodig is om de stroom naar de gloeilamp te circuleren, is dat de veldstroom varieert.

Wanneer het magnetische veld in de loop van de tijd varieert, kunnen we het uitdrukken als:

B = B (T).

Door het gebied van de spase constant te houden en het onder een constante hoek te laten vasthouden, die in het geval van de figuur 0º is, dan:

 Voor de lus van figuur 1 (cos 0º = 1):

Spase met variabel gebied

Als u het spase -gebied kunt wijzigen, waardoor de oriëntatie wordt bevestigd en in het midden van een constant veld wordt geplaatst, wordt de geïnduceerde FEM gegeven door:

Een manier om dit te bereiken is om een ​​balk te plaatsen die op een bepaalde snelheid op een geleidende rail glijdt, zoals weergegeven in de volgende figuur.

Kan u van dienst zijn: ío (satelliet) figuur 3. Schuifgenerator. Bron: Serway, r. Natuurkunde voor wetenschap en engineering.

De balk en de rail, plus een lamp of een weerstand die is verbonden met de bestuurdersdraad, vormen een gesloten circuit in de vorm van rechthoekige spase.

Bij het glijden van de balk, de lengte X verhoogt of neemt af, en daarmee verandert het gebied van de lus, wat voldoende is om een ​​variabele stroom te creëren.

Variatie van de magnetische flux door rotatie

Zoals we al eerder zeiden, als de hoek tussen B En het normaal van de lus is gevarieerd, de veldstroom verandert volgens:

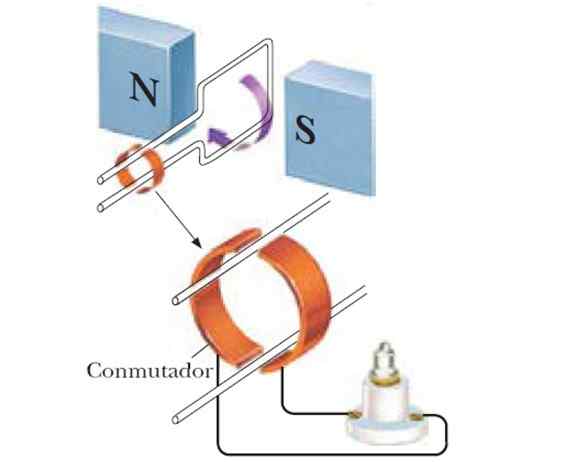Figuur 4. Als de lus wordt gedraaid tussen de polen van een magneet, wordt een sinusvormige generator verkregen. Bron: f. Zapata.

Een sinusvormige generator wordt dus verkregen, en als een enkel aantal spoelen wordt gebruikt, is de geïnduceerde FEM groter:

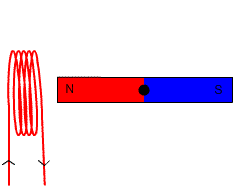Figuur 5. In deze generator wordt de magneet gedraaid om de stroom in de spoel te induceren. Bron: Wikimedia Commons.

Oefening opgelost

Een cirkelvormige spoel van N -ronden en radio R, draait hoekig ω in het midden van een magnetisch veld van grootte B. Zoek een uitdrukking voor de maximaal geïnduceerde FEM in de spoel.

Oplossing

De uitdrukking voor de door rotatie veroorzaakte FEM wordt toegepast wanneer de spoel N -ronden heeft, wetende dat:

-Het spoelgebied is a = πr²

-De hoek θ varieert afhankelijk van de tijd als θ = ωt

Het is belangrijk om rekening te houden met dat θ = ωt voor het eerst wordt vervangen in de wet van Faraday en Dan Het is afgeleid van de tijd:

ε = -nba (cos θ) '= -nb (πr²)).[cos (ωt)] '= nbω (πr²) Sen (ωt)

Aangezien de maximale FEM wordt gevraagd, gebeurt dit wanneer sen ωt = 1, dus ten slotte:

ε_maximaal = Nbω (πr²))

Referenties

1. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 6. Elektromagnetisme. Uitgegeven door Douglas Figueroa (USB).
2. Giambattista, een. 2010. Natuurkunde. Tweede druk. McGraw Hill.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. ED. Prentice Hall.
4. Resnick, r. 199999. Fysiek. Vol. 2. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 2.