Multiplicatieve omgekeerde uitleg, voorbeelden, oefeningen opgelost
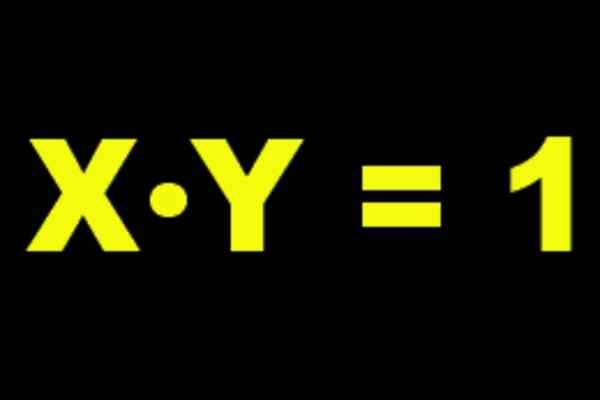
- 4292
- 664
- Aaron Okuneva
Het wordt begrepen door Omgekeerd multiplicatief van het ene getal, een ander getal dat vermenigvuldigde met de eerste resultaten in het neutrale element van het product, dat wil zeggen de eenheid. Als je een echt nummer hebt naar dan wordt zijn multiplicatieve inverse aangeduid door naar-1, En het is vervuld dat:
a a-1 = A-1 A = 1
Meestal het nummer naar Het behoort tot de reeks reële getallen.
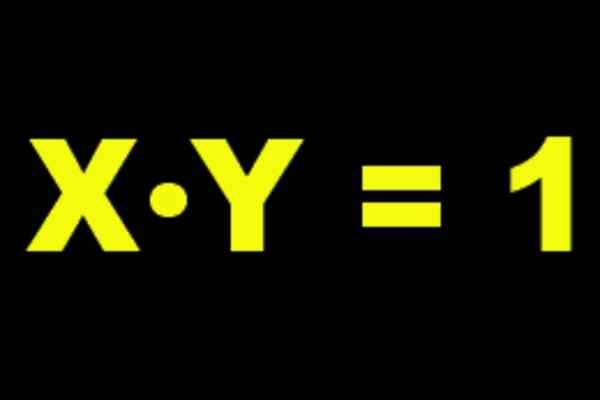 Figuur 1. En het is inverse multiplicatief van X en X is een multiplicatieve omgekeerde van Y.
Figuur 1. En het is inverse multiplicatief van X en X is een multiplicatieve omgekeerde van Y. Als we bijvoorbeeld nemen A = 2, Dan is je multiplicatieve inverse 2-1 = ½ Omdat het volgende is geverifieerd:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Naar de Omgekeerd multiplicatief van een nummer wordt ook de wederkerig, Omdat de multiplicatieve inverse wordt verkregen door de teller en de noemer uit te wisselen, bijvoorbeeld de multiplicatieve omgekeerde van 3/4 is 4/3.
Als algemene regel kan worden gezegd dat voor een rationeel nummer (P/Q) Uw multiplicatieve inverse (P/Q)-1 Het is wederzijds (Q/P) Zoals hieronder kan worden geverifieerd:
(P/Q) ⋅ (P/Q)-1 = (p/q) ⋅ (q/p) = (p⋅ q)/(q⋅ p) = (p⋅ q)/(p⋅ q) = 1
De multiplicatieve inverse bestaat niet in de numerieke set van de gehele getallen, Als bijvoorbeeld het gehele nummer 2 wordt ingenomen, zou het multiplicatieve omgekeerde volgens wat hierboven werd gezien ½ zijn, maar een ½ is geen geheel getal.
Er is ook de multiplicatieve omgekeerde van het nulelement van vermenigvuldiging. Met andere woorden, het nulnummer (0), het nulelement van de vermenigvuldigingsbewerking, heeft geen multiplicatief omgekeerd, omdat er geen getal is dat wordt vermenigvuldigd met nul van de eenheid.
Multiplicatief inverse bestaat in rationele getallen, in reële getallen en complexe getallen.
Multiplicatieve omgekeerde voorbeelden
voorbeeld 1
Zoek de 3/2 multiplicatieve omgekeerde en verifieer dat het de eigenschap van multiplicatieve gehele getallen voldoet.
Kan u van dienst zijn: Coplanares -punten: vergelijking, voorbeeld en opgeloste oefeningenVolgens de hierboven gegeven regel wordt de multiplicatieve inverse van (3/2) (2/3) op deze manier uitgewisseld. Om de vermenigvuldiging van de twee nummers te verifiëren wordt uitgevoerd:
(3/2) ⋅ (2/3) = (3 ⋅ 2)/(2 ⋅ 3) = 6/6 = 1.
Om twee fractionele getallen te vermenigvuldigen, vermenigvuldigt u eenvoudig de teller van de eerste door de tweede teller om de resultaatnummer te verkrijgen.
Om de noemer van een product van fractionele getallen te verkrijgen, gaat u op een vergelijkbare manier door, dat wil zeggen dat de noemers met elkaar worden vermenigvuldigd en het resultaat is de product noemer. In ons voorbeeld is het geverifieerd dat de teller van het product van het aantal en zijn wederkerige 6 is en de noemer is 6, waardoor fractie 6/6 achterblijft dat 1 is.
Voorbeeld 2
De multiplicatieve omgekeerde van -5 moet niet worden verward met zijn symmetrische (+5) die soms rekenkundige inverse wordt genoemd. De multiplicatieve inverse zal als volgt worden verkregen:
(-5) ⋅ x = 1
Waarbij x de multiplicatieve inverse is die moet worden verkregen. Een mogelijke procedure bestaat uit het opruimen van de onbekende x. AS (-5) vermenigvuldigt de onbekende X in het linker lid, dan gebeurt het dat het rechterlid deelt:
X = 1 / (-5)
Zoals bekend is + tussen - het is - dan wordt uiteindelijk X verkregen:
X = - ⅕ .
Concluderend - ⅕ is de multiplicatieve omgekeerde van -5.
Voorbeeld 3
Krijg de multiplicatieve omgekeerde van -√2. Stel dat de multiplicatieve inverse x is, dan moet -√2 vermenigvuldigen met X de eenheid zijn, een voorwaarde die we hieronder opleggen:
-√2 ⋅ x = 1
Beide leden worden gedeeld door -√2 om te verkrijgen:
(-√2 ⋅ x) / (--Z2) = 1 / (--Z2)
Het eerste lid is vereenvoudigd -"resterend:
Het kan u van dienst zijn: standaardramingfout: hoe het wordt berekend, voorbeelden, oefeningenX = 1 / (-√2)
Deze uitdrukking kan worden gerationaliseerd, dat wil zeggen, het elimineren van de root van de noemer, vermenigvuldigend in de teller met (-√2) en in de noemer voor dezelfde hoeveelheid zodat het resultaat niet wordt gewijzigd:
X = (-√2) / [(--Z 2) (-√2)] =-(√2 / 2)
Concluderend - (√2/2) is de multiplicatieve omgekeerde (-√2).
Voorbeeld 4
Ga uit van een getal x, krijg je multiplicatieve omgekeerde en vertegenwoordig deze grafisch.
In dit geval is het een functie f (x) = x, het verkrijgen van de multiplicatieve inverse is het vinden van de functie g (x) zodanig dat vermenigvuldigd is met de eerste van de eenheid van de eenheid. De G -functie is de wederzijdse functie van F en moet op geen enkele manier worden verward met zijn omgekeerde functie.
Met andere woorden, de multiplicatieve omgekeerde van X is een en zodanig dat het volgende is vervuld:
x ⋅ y = 1
Waar te wissen en te hebben:
y = 1/x.
Het bovenstaande wordt aldus geïnterpreteerd als een waarde van X, de vorige formule geeft ons zijn multiplicatieve omgekeerde.
Het is mogelijk om zijn grafische weergave te maken zoals weergegeven in de volgende figuur:
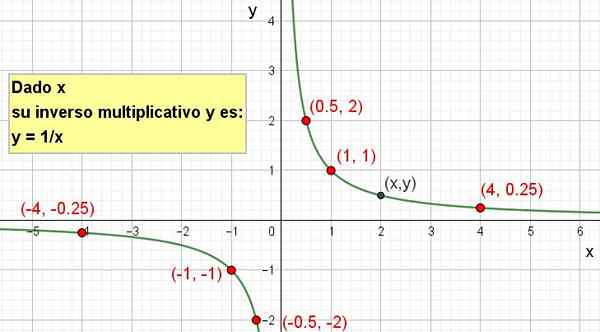 Figuur 2. De multiplicatieve inverse van x is y = 1/x.
Figuur 2. De multiplicatieve inverse van x is y = 1/x. Opdrachten
Oefening 1
Gegeven x = 2 - √2, krijg je multiplicatieve omgekeerde en.
Oplossing:
Zodat en het is een multiplicatieve x x
x ⋅ y = 1
X wordt vervangen door de waarde ervan:
(2 - √2) ⋅ y = 1
Dan wordt het gewist en:
y = 1 / (2 - √2)
Om het resultaat te rationaliseren vermenigvuldigt de teller en noemer met zijn geconjugeerde binomiaal:
y = (2 + √2) / ((2 + √2) (2 - √2)))
In de noemer wordt een opmerkelijk product erkend dat het product van een som voor een verschil wordt genoemd, wat het verschil is van de vierkanten. Op deze manier verdwijnt de wortel in de noemer.
y = (2 + √2) / (2^2 - (√2)^2)
Kan u van dienst zijn: proportieDe krachten oplossen:
y = (2 + √2) / (4 - 2)
Vereenvoudiging:
y = (2 + √2) / 2
Oefening 2
Verkrijg de multiplicatieve inverse (1/a + 1/b) waarbij a en b verschillende reële getallen zijn.
Oplossing:
We roepen en de multiplicatieve inverse van (1/a + 1/b), zodat de volgende vergelijking moet worden vervuld:
En ⋅ (1/a + 1/b) = 1
De variabele wordt gewist en:
Y = 1/(1/a + 1/b)
De noemer is opgelost:
Y = 1 / ((b + a) / a b)
Zoals bekend over de regels van de algebra, gaat de noemer van de noemer naar de teller:
Y = (a b) / (b + a)
Het is bevolen eindelijk te verkrijgen:
(a b)/(a + b), wat de multiplicatieve inverse is van (1/a + 1/b).
Oefening 3
Verkrijg de multiplicatieve inverse (a - b) / (a^2 - b^2).
Oplossing:
Bedenk dat de multiplicatieve inverse ook de wederzijdse wordt genoemd omdat het alleen wordt verkregen om de teller en de noemer uit te wisselen.
Dan zal de multiplicatieve inverse (a - b) / (a^2 - b^2) zijn:
(A^2 - b^2) / (a - b)
Maar deze uitdrukking kan worden vereenvoudigd als we, volgens de regels van algebra, erkennen dat de teller een verschil is van vierkanten dat voor een verschil als het product van een som kan worden afgezien:
((A + b) (a - b)) (a - b)
Omdat er een gemeenschappelijke factor (a - b) is in de teller en in de noemer gaan we verder met vereenvoudiging, eindelijk verkrijgen:
(a + b) dat is de multiplicatieve inverse (a - b) / (a^2 - b^2).
Referenties
- Bronnen, een. (2016). BASIS WISKUNDE. Een inleiding tot berekening. Lulu.com.
- Garo, m. (2014). Wiskunde: kwadratische vergelijkingen: hoe een kwadratische vergelijking oplossen. Marilù Garo.
- Haeussler, E. F., & Paul, r. S. (2003). Wiskunde voor administratie en economie. Pearson Education.
- Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Wiskunde 1 september. Drempelwaarde.
- Kostbaar, c. T. (2005). Wiskundecursus 3o. Redactionele progreso.
- Rock, n. M. (2006). Algebra I is gemakkelijk! Zo makkelijk. Team Rock Press.
- Sullivan, J. (2006). Algebra en trigonometrie. Pearson Education.

