Lineaire interpolatie

We leggen uit wat de lineaire interpo is, de formules, hoe te doen, met voorbeelden en oefeningen opgelost

Wat is lineaire interpolatie?

De Lineaire interpolatie Het bestaat uit het schatten van de locatie van een punt binnen een numeriek interval, ervan uitgaande dat de extreme waarden van dit interval verenigd zijn door een lijn. Bekend de vergelijking van deze lijn, is het mogelijk om het onbekende punt te vinden.

Het idee is geprestatiek in de volgende figuur, die een benadering van de grafiek van een functie tussen punten A en B toont. Ervan uitgaande dat deze punten dichtbij zijn, is het mogelijk om de curve te benaderen die hen door een lijn verenigt en zo de tussenliggende punten vindt.

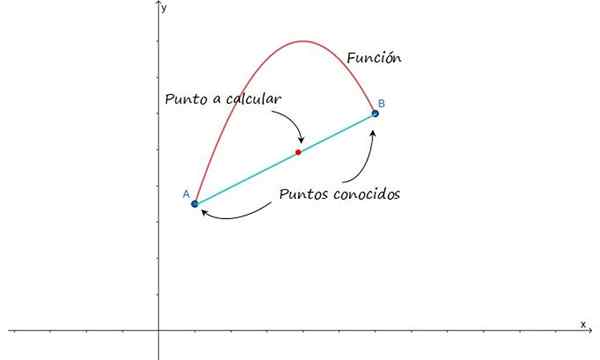Figuur 1.- Om een ​​lineaire interpolatie tussen punten A en B te maken, moet worden aangenomen dat ze door een lijn verenigd zijn . Bron: f. Zapata.

U kunt ook de curve benaderen die de punten verbindt die wordt gegeven door middel van een kwadratische functie of een andere polynoom. De lijn heeft echter het voordeel van zijn wiskundige eenvoud, dus het is gemakkelijk te hanteren, hoewel het de eenvoudigste interpolatie van allemaal is, is het mogelijk dat het resultaat niet zo nauwkeurig is als degene die is verkregen door andere functies te gebruiken.

Formules

Er zijn twee coördinaatpunten [x_of, F (x_of)] en [x₁, F (x₁)] waaronder het punt [x, g (x)], waarvan de coördinaten gewenst zijn te weten.

De eerste stap bestaat uit het samenvoegen van de bekende punten via een lijnsegment, waarop de coördinaten van het punt een berekening worden gevonden.

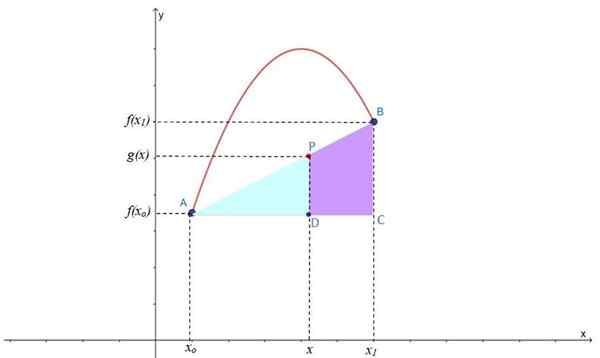Figuur 2.- Lineaire interpolatie om punt P te vinden op de interpoching -lijn G (x), gelegen tussen punten A en B van F (x). Bron: f. Zapata.

Zoals u kunt zien, worden twee rechthoeken gevormd: ABC en APD, die ook een acute hoek gemeen hebben, dus ze zijn vergelijkbare driehoeken, waarop de Thales -stelling kan worden toegepast:

Het kan u van dienst zijn: analytische geometrie

Door de maat van de segmenten te vervangen volgens de grafiek, wordt de volgende relatie verkregen:

Van daaruit gaan we verder naar G (x):

 Roeping:

F₁(X₁) = y₁ ; F_of(X_of) = y_of ; g (x) = y

De topvergelijking wordt omgezet in:

Foutenbereik

Wanneer een functie met deze methode nadert, wordt het foutniveau gegeven door de absolute waarde van het verschil tussen de functie f (x) en de interpolatielijn g (x):

Error = │f (x) - g (x) │

Hoe lineaire interpolatie te maken?

Het uitvoeren van een lineaire interpolatie is heel eenvoudig, je moet gewoon deze stappen volgen:

Stap 1

Bepaal het onbekende punt P (x, y).

Stap 2

Stel de twee punten vast die het interval beperken waar de te berekenen waarde is, dat wil zeggen de punten (x x_of,En_of) en (x₁, En₁)).

Stap 3

Vervang alle waarden in de vergelijking:

En bereken het resultaat.

Voorbeelden van lineaire interpolatie

voorbeeld 1

U wilt de geschatte waarde van LN 3 vinden via lineaire interpolatie, gezien de volgende waarden:

ln 2 = 0.693147 en ln 4 = 1.386294

Vergelijk het resultaat met de waarde van LN 3 verkregen via een calculator en bepaal de gepleegde marge.

• Stap 1

Om de geschatte waarde van LN 3 te vinden, moet u de volgende manier verdergaan: Ten eerste wordt het onbekende vastgesteld, wat Y = Ln 3 is, naast de overeenkomstige waarde van "X": X = 3. Dit is het punt dat u wilt berekenen: (3, ln 3).

• Stap 2

Dan moet u de limietpunten van het interval vaststellen met de bekende waarden. Het wordt gevraagd dit te doen met de volgende paar punten:

• Ondergrens: [x_of = 2; En_of = ln 2 = 0.693147]
• Bovengrens: [x₁ = 4; En₁ = ln 4 = 1.386294]

• Stap 3

De waarden bepaald in stappen 1 en 2 worden zorgvuldig vervangen in de vergelijking om het resultaat van de benadering van LN 3 te genereren:

Kan u van dienst zijn: hoeveel oplossingen hebben een kwadratische vergelijking?

De reële waarde van ln 3 verkregen door calculator is:

ln 3 = 1.098612

En de foutenmarge is:

Error = │1.098612 - 1.03971 │ = 0.059

De procentuele fout van de interpolatie wordt berekend door de fout tussen de reële waarde van LN3 te delen en met 100 %te vermenigvuldigen:

Percentagefout = (reële fout/waarde) × 100 = (0.059/1.098612) × 100% = 5.4%

Voorbeeld 2

Nu wilt u de geschatte waarde van LN 3 vinden door lineaire interpolatie, deze twee waarden bekend:

LN 2.5 = 0.916291 en ln 3.5 = 1.252763

Bepaal ook de overeenkomstige fout en vergelijk met de resultaten van het vorige voorbeeld.

• Stap 1

Nogmaals, het onbekende punt is:

y = ln 3, x = 3

• Stap 2

• Ondergrens: [x_of = 2.5; En_of = Y_of = ln 2.5 = 0.916291]
• Bovengrens: [x₁ = 3.5; En₁ = ln 3.5 = 1.252763]

• Stap 3

Onderzoek naar de waarde die de calculator wordt aangeboden:

ln 3 = 1.098612

Het foutniveau wordt in dit geval bepaald, wat resulteert:

Error = │1.098612 - 1.084527 │ = 0.014

De procentuele fout is in dit geval ≈ 1.3 %. In vergelijking met het foutniveau van voorbeeld 1, is de nieuwe waarde nauwkeuriger, omdat het gekozen interval dat wordt gekozen om te interpolar lager zijn.

Opgeloste oefeningen

Oefening 1

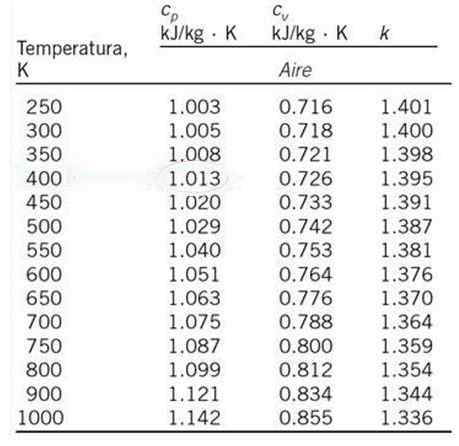
Bereken, door lineaire interpolatie, de specifieke warmte van de lucht bij constante druk C_P  en temperatuur van 530 K, beginnend bij de onderstaande tabel met waarden.

• Oplossing

In de resolutie van veel problemen is het gebruikelijk dat de gezochte waarde niet precies lijkt in de tabel met waarden die bij de hand liggen. Een alternatief is om de waarde te kiezen die het dichtst bij de gewenste is, maar vaak is een lineaire interpolatie voldoende om een ​​veel betere aanpak te vinden.

Kan u van dienst zijn: tekenen van groepering

De waarde van C_P Een 530 K verschijnt niet in de bijgevoegde tabel, maar een lineaire interpolatie kan worden gemaakt met de respectieve specifieke warmte op 500 K en 550 K, die de temperaturen zijn die het dichtst bij 530 K staan ​​en wiens specifieke hitten verschijnen in de getoonde tabel.

De respectieve specifieke warmtewarmtes voor deze temperaturen zijn:

T_of = 500 K; C_po = 1.029 kJ /kg ∙ k

T₁ = 550 K; C_P1 = 1.040 kJ /kg ∙ k

En het onbekende is het punt (500k, c_P))

Vervangen in de formule van de hierboven gegeven lineaire interpolatie, met t op het toneel van de variabele "x" en c_P In plaats van "y" heb je:

Oefening 2

De belasting toegepast op een veer (in kilopondios) produceert de volgende verlengingen (in millimeters) volgens de getoonde tabel:

Bereken verlenging wanneer de belasting 12 is.6 kp.

• Oplossing

Laat en de waarde van de rek die werd gevraagd wanneer de belasting c = 12 is.6 kp. Het onbekende punt is (12.6, y), wat een van de punten is:

C_of = 10 kp; En_of = 105 mm

C₁ = 15 kp; En₁ = 172 mm

Het blijft alleen om de waarden in de vergelijking te vervangen:

Voorgestelde oefening

Bereken de specifieke warmtewarmte tot een constant volume voor een temperatuur van 727 K, met behulp van lineaire interpolatie en de tabel met effecten van de oefening opgelost 1.

Referenties

1. Rafa Vilchez Academy. Hoe lineaire interpolatie uit te voeren. Hersteld van: Academiraafavilchez.com
2. Chapra, s. 2007. Numerieke methoden voor ingenieurs. 5e. Editie. McGraw Hill.
3. Khan Academy. Wiskunde van lineaire interpolatie. Hersteld van: Khanacademy.borg.
4. Het onderwijsleven. Lineaire interpolatieformule. Hersteld van: TheDucationLife.com
5. X-engineer. Lineaire interpolatie en extrapolatie met rekenmachine. Hersteld van: x-engineer.borg.